
Читайте также:
|
| Решите задачу | Решите задачу | Решите задачу | |
| * | Точка S удалена от каждой стороны правильного треугольника на 15 см, а от его плоскости на 10 см. Найдите длину стороны треугольника. | К плоскости прямоугольного треугольника MNP, где угол P - прямой, проведен перпендикуляр SN, SM=13 см, угол MNP =30º; MP=5 см. Вычислите расстояние от точки S до прямой MP. | К плоскости равностороннего треугольника АВС, площадь которого равна 48 см2 проведен перпендикуляр АS. ВС=10 см; АК=5 см. Найдите расстояние от точки S до прямой ВС. |
| Угол А остроугольного треугольника АВС равен 45º, ВС=12 см. Точка М удалена от его плоскости на 6 см и находится на одинаковом расстоянии от всех вершин треугольника. Вычислите расстояние МА, МВ и МС. | Через точку пересечения диагоналей квадрата АВСВ проведен перпендикуляр МО к его плоскости, равный 15 см. Вычислите расстояние от точки М до стороны квадрата если АВ=16 см. | Стороны прямоугольника АВСD равны 6 см 6 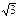 см. К плоскости прямоугольника через точку пересечения его диагоналей проведен перпендикуляр ОК=6 см. Найдите углы между плоскостью прямоугольника и прямыми КА и КВ. см. К плоскости прямоугольника через точку пересечения его диагоналей проведен перпендикуляр ОК=6 см. Найдите углы между плоскостью прямоугольника и прямыми КА и КВ.
| |
| Точка М одинаково удалена от всех сторон треугольника АВС. Расстояние от точки М до его плоскости равно 12 см, а радиус вписанный в треугольник окружности равен 5 см. Вычислите расстояние от точки М до сторон треугольника. | Отрезок АМ, равный 12 см перпендикулярен плоскости треугольника АВС. Вычислите расстояние от точки М до прямой ВС, если АВ=АС=20 см, ВС=24 см. | Через точку А к плоскости α проведены наклонные АВ, АС и перпендикуляр АО, АВ=6 см. Углы между прямыми АВ, Аси плоскостью α равны соответственно 30º, 40º. Найдите длины перпендикуляра АО, наклонной АС и ее проекциями. | |
| Точка равноудаленная от всех вершин прямоугольника находится на расстоянии 8 см от его плоскости. Вычислите расстояние от этой точки до вершин прямоугольника, если его меньшая сторона 8 см, диагональ образует с большой стороной угол 30º. | К плоскости прямоугольника ABCD площадь которого равна 180см2 проведен перпендикуляр KD. Вычислите расстояние от точки К до сторон прямоугольника, если KD=12 см, ВС=20 см. | Через середину гипотенузы прямоугольного треугольника АВС проведен к его плоскости перпендикуляр КО, равный 8,5 см. ВС=8 см, АС=15 см. Вычислите углы между плоскостью треугольника и наклонными КА, КВ, КС. | |
Точка S удалена от каждой вершины квадрата на 10 дм. Вычислите расстояние от точки S до плоскости квадрата, если его сторона равна 6 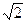 дм. дм.
| К плоскости прямоугольного треугольника АВС, где угол С=90º проведен перпендикуляр РВ, РА=13 см, угол АВС=30º; АС=5 см. Вычислите расстояние от точки Р до прямой АС. | Через вершину М равностороннего треугольника МРК проведен к его плоскости перпендикуляр МС. Угол между прямой СК и плоскостью треугольника равен 60º, РК=24 см. Найдите углы перпендикуляра МС и наклонной СР. |
Дата добавления: 2015-08-17; просмотров: 604 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение показательных уравнений и неравенств | | | Нахождение двугранных углов |