| |
|
|
|
| | Решите задачу
| Решите задачу
| Решите задачу
|
| *
| Основание пирамиды SABC – прямоугольный треугольник с прямым углом B, SO – высота пирамиды. Построить ЛУДУ при ребрах AB и BC.
| Через вершину квадрата АВСD проведён к его плоскости перпендикуляр DМ равный 10см. Угол между плоскостями АВС и MDC равен 45º. Найти площадь треугольника ВСM
| Через вершину D тупого угла ромба АВСD проведен перпендикуляр DK равный 9 см. Диагонали ромба равны 12 см и 16 см. Вычислить углы между плоскостями АВС и KВС
|
|
| Основание пирамиды MNPK-прямоугольный треугольник NPK с прямым углом К. Высота МО падает в центр описанной окружности. Постройте ЛУДУ при ребрах NK и PK.
| Отрезки АС и ВС, лежащие в гранях прямого двугранного угла перпендикулярны к его ребру. Вычислите расстояние между точками А и В, если АС=10 см, ВС=24 см
| Дан треугольник MNP, у которого угол М равен 90º; MN=9 см. Через сторону РМ проведена плоскость α под углом 60º к плоскости треугольника MNP. Найти расстояние от вершины N до плоскости α.
|
|
| Основанием пирамиды SABCD является квадрат. Высота SO падает в точку пересечения диагоналей. Построить ЛУДУ при ребрах АВ и ВС.
| Точка К, лежащая в грани двугранного угла удалена от другой грани на 12 см, а от ребра на 8 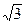 см. вычислите величину двугранного угла. см. вычислите величину двугранного угла.
| Катет прямоугольного треугольника APN с прямым углом N лежит в плоскости α, а угол между плоскостями α и APN равен 60º. Найти расстояние от точки Р до плоскости α, если AN=12 см, АР=13 см.
|
|
| Основание пирамиды SABC – треугольник, у которого AB=BC, высотой служит ребро SB. Построить линейный угол двугранного угла при ребре AC.
| В грани двугранного угла равного 30º расположена точка A. Вычислить расстояние от точки A до второй грани, если она удалена от ребра двугранного угла на 16 см.
| Правильные треугольники ABC и DBC расположены так, что вершина D проектируется в центр треугольника ABC. Найти угол между плоскостями этих треугольников.
|
|
| Основание пирамиды SABC – прямоугольный треугольник с прямым углом ABC, SO – высота пирамиды. Построить линейные углы двугранных углов при ребрах AB и BC.
| Угол между плоскостями α и β равен 60º. Точка С принадлежит ребру этого угла, отрезки АС и ВС перпендикулярны этому ребру и равны соответственно 5 см и 8 см. Вычислить расстояние между концами этих перпендикуляров.
| Через сторону AB треугольника ABC проведена плоскость α, расстояние от вершины C до плоскости α равно 7,5 см. Найти угол между плоскостью α и плоскостью треугольника, если AB=16 см., AC=BC=17 см.
|

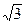 см. вычислите величину двугранного угла.
см. вычислите величину двугранного угла.