Дана функция . а) исследовать функцию на экстремум;

а) исследовать функцию на экстремум;

б) найти наибольшее и наименьшее значения функции в замкнутой области 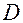, заданной системой неравенств 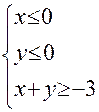, сделать чертеж области.

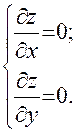
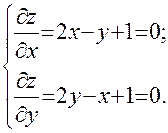
Решение. а) Найдем стационарные точки функции из системы уравнений: 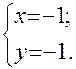Следовательно,

Точка 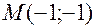- стационарная точка функции. Вычислим значения частных производных второго порядка в точке .

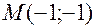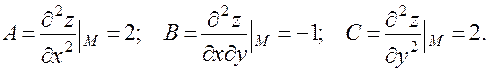
Составим дискриминант 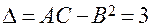. Так как 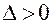, то экстремум есть, так как 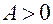, то 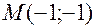- точка минимума.

б) Построим область 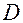, заданную системой неравенств .

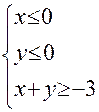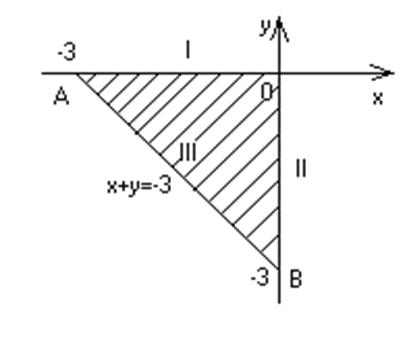
Это треугольник с вершинами в точках О(0;0), А(-3;0), В(0;-3).

Наибольшее и наименьшее значения в замкнутой области 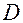функция 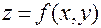может достигать в стационарных точках, принадлежащих области 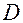и на границе области. Поэтому:

Вычислим значение функции в стационарной точке 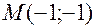, принадлежащей области : .

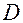Вычислим значения функции в точках О(0;0), А(-3;0), В(0;-3), которые являются точками «стыковки» различных участков границы области.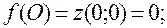

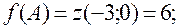
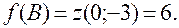
Вычислим значения функции в критических точках на границе области.

I участок: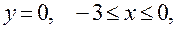

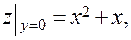
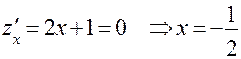- критическая точка, принадлежащая [-3;0].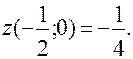

II участок: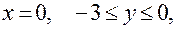

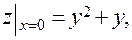
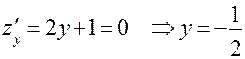- критическая точка, принадлежащая [-3;0].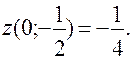

III участок: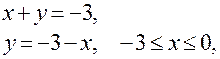

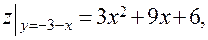
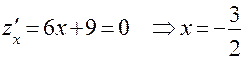- критическая точка, принадлежащая [-3;0].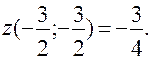

Из всех вычисленных значений выберем наибольшее и наименьшее: 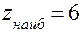в точках 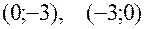, 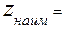-1 в точке .

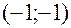Дата добавления: 2015-08-17