Волгодонск

Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ

Методические указания

К выполнению индивидуальных заданий

по теме:

«Функции нескольких переменных»

Волгодонск

Задача 1. Найти частные производные от функций:

а) .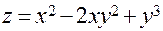

Решение. Частную производную 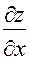находим как производную функции 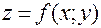по аргументу 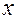в предположении, что . Поэтому,

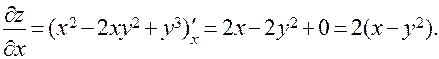
Аналогично,

б)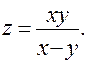

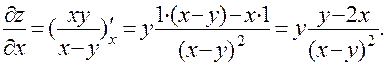
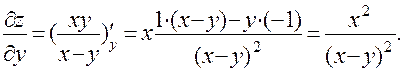
в)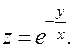

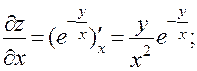
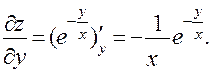
г)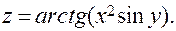

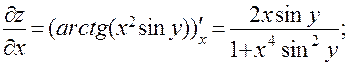
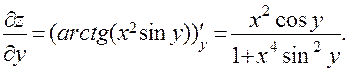
Задача 2. Продифференцировать сложную функцию:

а)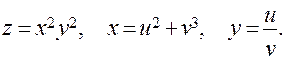

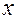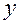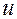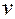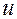Решение. Так как и зависят от переменных и , то функция в конечном итоге зависит от переменных и 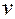, и ее частные производные можно найти по формулам:

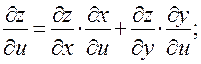
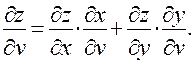
Следовательно,

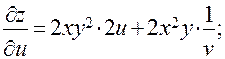
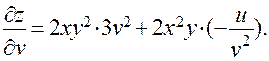
б) 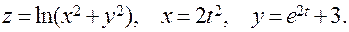Найти

Решение. Так как функция в конечном итоге зависит от одной переменной 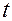, то ее производную можно найти по формуле:

Тогда,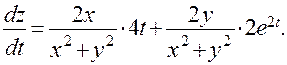

Задача 3. Дана функция 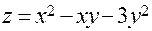и точки .

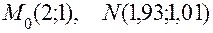а) найти полные дифференциалы функции 1-го и 2-го порядков;

б) вычислить значение 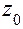функции в точке ;

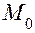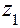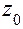в) вычислить приближенное значение функции в точке , исходя из значения функции в точке 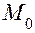и, заменив приращение функции при переходе от точки 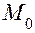к точке

дифференциалом;

г) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом;

д) составить уравнения касательной плоскости и нормали к поверхности 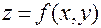в точке .

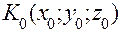Решение. а) Вычислим частные производные функции 1-го и 2-го порядков.

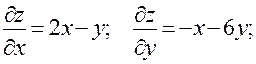
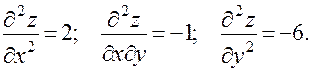
Тогда, полный дифференциал 1-го порядка равен:

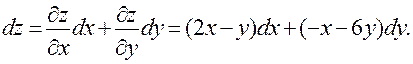
Полный дифференциал второго порядка:

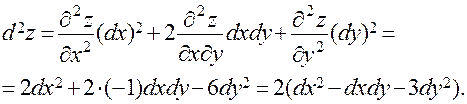
б) Вычислим значение функции в точке .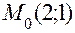

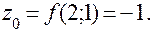
в) Вычислим значение функции в точке 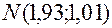с помощью микрокалькулятора: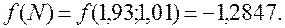

Вычислим приближенное значение функции в точке N с помощью дифференциала по формуле: 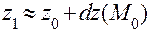, где дифференциал функции 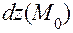приближенно равен приращению функции при переходе от точки 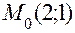к точке .

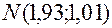Дифференциал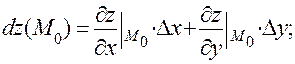

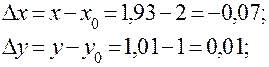
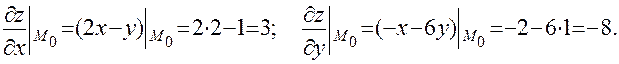
Тогда дифференциал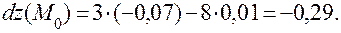

Получим приближенное значение функции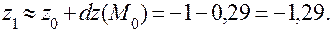

г) Оценим относительную погрешность вычисления:

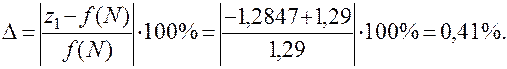
д) Составим уравнения касательной плоскости и нормали к поверхности 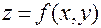в точке .

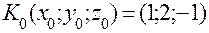Уравнение касательной плоскости имеет вид:

.

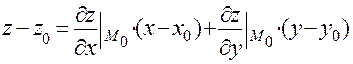Подставив в это уравнение значения частных производных в точке 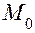и координаты точки 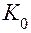, получим:

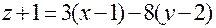. Окончательно, .

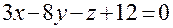Канонические уравнения нормали к поверхности, проходящей через точку 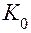, перпендикулярно касательной плоскости имеет вид: . Следовательно, имеем уравнения нормали .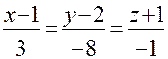

Дата добавления: 2015-08-17