Геостатические модели изменчивости геологических показателей

Если моделируемое поле признака является случайным однородным полем с конечным математическим ожиданием и дисперсией, то между автокорреляционной K(h) и структурной S(h) функциями справедливо следующее отношение:

2K(h)=S(∞) – S(h) или S(h)=2K(0)-2K(h), (4.33)

Где K(h)=M[(C(x)-m)(C(x+h)-m)], а

S(h)=M[C(x)-C(x+h)]².

Аналогичными соотношения будут справедливы и для их оценок. Выбор функции при оценке изменчивости не принципиален при сделанных предположениях и должен определяться простотой вычислительных процедур при нахождении оценок и подборе аналитической аппроксимирующей зависимости. Оценка структурной функции предпочтительнее, так как для нее относительно просто находятся числовые параметры по результатам экспериментальных оценок.

Рассмотрим некоторые практические аспекты оценки структурных функций и их аппроксимации аналитическими выражениями. Не вызывает затруднений оценка S(h), если разведочная сеть регулярна. Пусть известны значения показателя С(х_i, y_i) в узлах прямоугольной сети с размерами элементарной ячейки h_x*h_y. Тогда оценки S(h) для четырех различных направлений находятся по формулам:

· в направлении :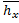

· в направлении :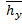

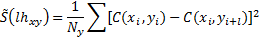
• в направлении :

• в направлении :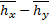

Оценки структурной функции (вариограммы) S(h), построенные для различных направлений, несут почти всю информацию об изменчивости характеристик поля, необходимую при решении задачи об оценке показателей, и ее погрешности в произвольной точке поля или в заданном объеме. Различие вариограмм, построенных для различных направлений, позволяет выявить геометрическую, зональную и функциональную анизотропии.

При наличии всех трех типов анизотропии аппроксимация вариограмм может быть сложной. Дело в том, что при анализе экспериментальных вариограмм следует учитывать, что функциональная анизотропия указывает на наличие закономерной составляющей (тренда) в размещении показателя и она проявляется в резком возрастании S(h) на больших расстояниях. Геометрическая анизотропия проявляется в подобии вариограмм для взаимно перпендикулярных направлений, причем коэффициент подобия равен коэффициенту анизотропии. Наличие зональной анизотропии связано с различным масштабом изменчивости для разных направлений, то есть значения S(h) существенно отличаются друг от друга на больших расстояниях. Оставшаяся часть будет характеризовать анизотропную составляющую изменчивости показателя.

Аппроксимация вариограмм проводится с помощью одной из моделей, приведенных в табл.4.17. При этом необходимо руководствоваться особенностями тех задач, для решения которых в дальнейшем будет использоваться структурная функция S(h). Например, для нахождения оптимальной оценки среднего содержания металла в блоке необходимо аппроксимировать S(h) на достаточно большом интервале изменения h. В этом случае удобнее всего использовать экспоненциальную или сферическую модели изменчивости.

В связи с задачами интерполяции, возникающими при вычерчивании изолиний с помощью ПК, необходимо более точно аппроксимировать S(h) в окрестности нуля. Для этих целей наиболее подходящая аппроксимационная модель – степенная. Преимущества степенной модели объясняются, что показатель в уравнении структурной функции

S(h) = 2 (4.35)

(0≤k≤2)

характеризует степень регулярности пространственной переменной. Чем ближе k к нулю, тем выше доля случайной составляющей изменчивости; при k=2 случайная составляющая отсутствует. При этом в представлении (4.35) отсутствует константа «эффекта самородков».

Таблица 1

Модели и уравнения собственных функций

Для определения параметров уравнения (4.35) удобно представлять оценку вариограмм S(h) в логарифмическом масштабе по обеим осям. В этом случае оценкой параметра k будет тангенс угла наклона графика S(h) к горизонтальной оси. Примеры расчета для экспериментальных вариограмм приведены на рис.2.

Для регулярных сетей опробования оценка структурных функций при неравномерном опробовании имеет свои особенности. В этом случае для оценки вариограммы строится гистограмма переменных расстояний h между всеми возможными парами точек (M_i, M_J) с использованием среднего расстояния h_ср. После этого квадраты разностей хС (M_i) – C(M_J)]² для всех пар, попадающих в один разряд, объединяются и усредняются. Простое усреднение правомочно, так как расстояния между соседними точками распределены приблизительно равномерно на отрезке [0, h_ср]. Подбор модели изменчивости и определение параметров модели проводятся, как и при равномерном опробовании. [1]

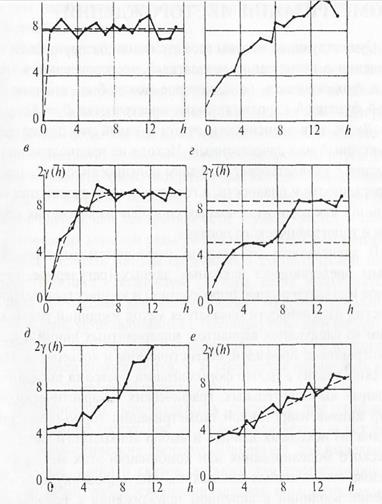
Рис.2. Вариограммы содержаний Мо(а) и WO₃ для Тырныаузского месторождения, а также Cu (в,г) и Ni (д,е) для различных участков Талнахского месторождения

Список литературы:

1. Ермолов В.А. Геология. Часть 2: Разведка и геолого-промышленная оценка месторождений полезных ископаемых. – 392с. 2005 г.

2. Домаренко В.А. Часть 2: Рациональная методика поисков и геолого-экономической оценки месторождений руд редких и радиоактивных элементов; ТПУ, 2012.

Дата добавления: 2015-08-17