Марковские случайные процессы

Предположим, что система может менять случайным образом свое состояние в некоторые моменты времени t ₁, t ₂, …,
t_i, … Последовательность принимаемых системой состояний называется случайным процессом (цепью).

Обозначим E_n, где n = 1, 2, … – множество возможных состояний системы, P_n (i) – вероятность нахождения системы в конкретном состоянии E_n в момент времени t_i.

Марковский процесс – это такой процесс, будущее состояние которого определяется только его состоянием в настоящий момент времени и не зависит от предыдущих состояний.

Поэтому, каждой паре состояний E_n, E_k можно поставить в соответствие условную вероятность P_nk того, что система будет находиться в состоянии E_k в момент t_{i +1} при условии, что в момент t_i она находится в состоянии E_n.

Цепь Маркова с непрерывным временем удобно изображать в виде графа состояний, узлы которого соответствуют возможным состояниям системы, а дуги графа – возможным одношаговым переходам между состояниями. Каждая дуга снабжается числом, равным вероятности соответствующего перехода, что иллюстрирует рис. 2.

Обозначим:

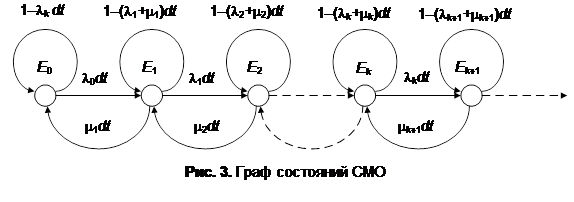
E_n – состояние системы, когда в ней находится n заявок;

l _n – интенсивность входного потока в состоянии E_n;

m _n – параметр закона распределения времени обслуживания в состоянии E_n.

Рассмотрим процесс функционирования системы на малом интервале времени (t, t + dt). На этом отрезке времени в системе могут произойти следующие переходы с соответствующими вероятностями:

· вероятность перехода E ₀ ® E ₀ определяется вероятностью отсутствия прихода заявок в течение интервала (t, t + dt) и равна (1 – l₀ dt);

· вероятность перехода E_n ® E_{n +1} определяется вероятностью прихода заявки и равна l _ndt;

· вероятность перехода E_n ® E_{n –1} определяется вероятностью обслуживания за время 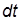одной заявки. При показательном законе обслуживания на выходе СМО имеем пуассоновский поток плотности m _n, в котором вероятность появления события на интервале 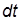равна m _ndt;

· вероятность остаться в текущем состоянии (переход E_n ® E_n) равна 1 – l _ndt – m _ndt, она определяется вероятностью составного события: за время dt заявка не придет и не будет обслужена.

Учитывая все перечисленные переходы и их вероятности, можно построить граф состояний, показанный на рис. 3.

Графу состояний соответствует матрица переходов

На рис. 4 представлен пример одноканальной СМО.

Для графа состояний этой СМО система уравнений имеет вид:

P (t + dt) = P (t) J, где

Уравнения вероятностей состояний в развернутом виде

Последние при dt ® 0 преобразуются в дифференциальные уравнения Колмогорова:

Эти уравнения могут быть решены при заданных начальных условиях, например P ₀(0) = 1, P_n (0) = 0, n ¹ 0. Из решения системы уравнений при следуют решения для стационарных (финальных) вероятностей состояний .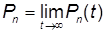

Решение системы линейных дифференциальных уравнений и построение временных характеристик в среде MathCAD выполняется с помощью тех же методов и средств, которые использовались для этих целей в лабораторной работе №1. Применительно к системе дифференциальных уравнений вероятностей состояний MathCAD-программа может выглядеть как на рис. 5.

	Рис. 5. Моделирование СМО в среде MathCAD

Прямой путь получения уравнения стационарного режима состоит в приравнивании нулю производных вероятностей состояний в системе дифференциальных уравнений Колмогорова и замене переменных P_n (t)на P_n. Для описываемой системы получим

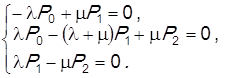
Кроме того, одно из линейно зависимых уравнений (любое) следует заменить уравнением нормировки. Окончательная система линейных алгебраических уравнений имеет вид:

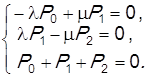
Эту систему необходимо решить средствами MathCAD.

---

Дата добавления: 2015-08-17