Поля геологических признаков

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ИНСТИТУТ ПРИРОДНЫХ РЕСУРСОВ

Кафедра «ГЭГХ»

Моделирование пространственных переменных

Выполнил:

студент группы 2670

Редькина Д.И.

Проверил:

доцент

Домаренко В.А.

Томск 2011

Оглавление

1. Поля геологических признаков

2. Метод математического моделирования пространственных переменных

3. Геостатические модели изменчивости геологических показателей

Поля геологических признаков

При изучении строения земной коры разведуемого или разрабатываемого месторождения геолога, горняка и обогатителя интересуют не только средние характеристики изменчивости и взаимосвязи наблюдаемых параметров, например, концентраций компонентов, но и закономерности их пространственных изменений в исследуемых объемах недр. Статические модели для этих целей непригодны, поскольку любой статический показатель отражает лишь средний уровень изменчивости изучаемого свойства, независимо от пространственного размещения пунктов опробования, в то время, как закономерности их пространственного размещения могут оказаться абсолютно различными, что иллюстрируется схематическими графиками на рис.1.

Следует также помнить, что статические характеристики обеспечивают объективные оценки уровня наблюдаемой изменчивости признака только в случаях, когда выборочные данные представляют собой совокупность независимых случайных величин. Указанные недостатки статических методов определенной мере устраняются с помощью математического моделирования полей геологических признаков на основе современных математических признаков.

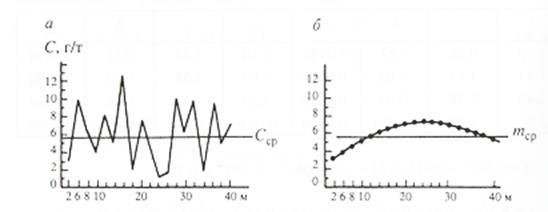
Рис.1. Графики изменения параметров по золотоносной жиле:

а – содержание золота; б – мощность жилы.

Полем геологического признака называется пространство недр (или часть его), каждая точка которого характеризуется значением геологического показателя (признака).

Такое определение аналогично понятию скалярного поля в математике. Если с пространством недр связана прямоугольная система координат, то каждая ее точка имеет координаты x, y, z. Поле геологического признака U считается заданным, если в каждой точке пространства задана функция U=f(x,y,z). Ясно, что в одной и той же части пространства могут быть определены несколько функций для различных геологических показателей. Наряду с трехмерными полями геологических признаков будем также рассматривать двумерные и одномерные поля. Например, мощность рудной залежи m есть функция двух координат m=f(x,y).

В зависимости от природы свойства недр, характеризующего показатель U, всегда можно указать возможные значения, которые может принимать данная переменная. Как правило, числовые значения признака U могут изменяться непрерывно в некотором промежутке. Например, содержание полезного компонента, измеренное в процентах, может иметь значения от 0 до 100. Нижняя граница интервала может отличаться от нуля, если речь идет о бортовом содержании.

Для более полного описания свойства недр, наряду с полями признаков, возможные значения которых непрерывны, полезно ввести в рассмотрение поля геологических признаков, которые могут обладать лишь конечным числом значений. В простейшем случае число возможных значений равно двум. В связи с описанием таких полей важное значение имеет понятие индикаторной переменной I(x,y,z) (или просто индикатора), которая принимает да возможных значения - 0 и 1.

Обычно индикатор связывается с одним из показателей непрерывного типа следующим образом:

I_U(x,y,z)={ 1при f(x,y,z)≥U_O

{ 0 при f(x,y,z)<U_O

Геометрический смысл индикатора I_u заключается в следующем. Пусть, U=f(x,y,z) – содержание основного компонента, U₀ – минимальное промышленное содержание. Тогда область недр, в каждой точке которой среднее значение индикатора I_u равно единице, будет отвечать балансовым запасам. При изменении технико-экономических условий значение U₀ также изменится, а это, в свою очередь, приведет к преобразованию поля индикатора I_u. Аналитические операции над переменной I_u позволяют установить в рассмотренном примере контуры балансовых запасов.

При исследовании месторождения поля геологических признаков неизвестны. Геологоразведочные работы позволяют установить числовые значения показателя U_k=f(x,y,z) в ограниченном числе точек M_k по результатам прямых измерений (опробования). В общем виде основная задача при изучении свойств месторождения полезного ископаемого может быть сформулирована следующим образом: по известным значениям показателя U_k конечном числе пунктов опробования восстановить значения.

В такой постановке математическим аналогом является задача интерполяции функции. Результатом ее решения будет математическая модель поля геологического признака U=f(x,y,z). Такая модель всегда будет приближенной, так как, с одной стороны, результаты опробования сопровождаются погрешностями, а с другой – любая интерполяционная процедура сопровождается методическими погрешностями. Соотношение между этими двумя типами погрешностей может быть различным. В некоторых случаях разумно пренебречь техническими погрешностями опробования при выборе метода интерполяции.

Итак, для того чтобы построить математическую модель поля геологического признака, необходимо использовать соответствующий метод интерполяции. К настоящему времени в прикладной математике разработано большое число интерполяционных методов применительно к различным задачам из разных областей науки и техники.

Дата добавления: 2015-08-17