
|
Читайте также: |

| 
| ||

| |||

| |||

|
Тема: Непрерывность функции, точки разрыва
Функция 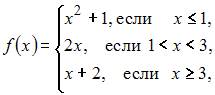 не является непрерывной на отрезке …
не является непрерывной на отрезке …

| 
| ||

| |||

| |||

|
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …

| 
| ||

| |||

| |||

|
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …

| 0,13 | ||
| 0,065 | |||
| 3,9 | |||
| 0,7 |
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция  представлена таблицей:
представлена таблицей:

Тогда график многочлена, интерполирующего эту функцию, пересекает ось 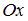 в точке с абсциссой …
в точке с абсциссой …

| 5,5 | ||
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии  на
на 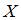 имеет вид
имеет вид 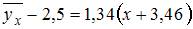 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 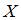 равно …
равно …

| 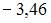
| ||

| |||
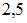
| |||
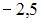
|
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …

| 11,25 | ||
| 19,5 | |||
| 21,25 |
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал  для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …

| 1,12 | ||
| 0,01 | |||
| 2,24 | |||
| 13,56 |
Тема: Градиент скалярного поля
Модуль градиента скалярного поля  в точке
в точке  равен …
равен …

| 
| ||

| |||
Тема: Норма вектора в евклидовом пространстве
Даны векторы 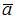 и
и  , угол между которыми равен
, угол между которыми равен  . Тогда проекция вектора
. Тогда проекция вектора 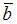 на вектор
на вектор 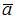 равна …
равна …

| 
| ||
| – 1 | |||
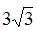
|
Тема: Элементы теории множеств
Даны три множества: 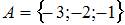 ,
,  и
и 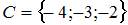 . Тогда число элементов множества
. Тогда число элементов множества  равно …
равно …
| 1 | |
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент  в разложении в ряд Фурье функции
в разложении в ряд Фурье функции  на интервале
на интервале  равен …
равен …

| 
| ||
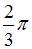
| |||

| |||

|
Тема: Периодические функции
Период функции  равен …
равен …

| 
| ||
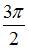
| |||

| |||

|
Тема: Комплексные числа и их представление
Показательная форма записи комплексного числа  имеет вид …
имеет вид …

| 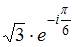
| ||

| |||

| |||

|
Тема: Однородные дифференциальные уравнения
Общий интеграл дифференциального уравнения  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
однородным относительно 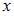 и и 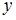 дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Тема: Системы линейных уравнений
Решение системы линейных уравнений  методом Крамера может иметь вид …
методом Крамера может иметь вид …

| 
| ||

| |||

| |||

|
Тема: Умножение матриц
Матрица 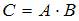 , где
, где  и
и  . Тогда элемент
. Тогда элемент  равен …
равен …

| |||
| – 3 | |||
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции  в точке
в точке 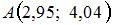 , вычисленное с помощью полного дифференциала, равно …
, вычисленное с помощью полного дифференциала, равно …

| 
| ||

| |||
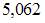
| |||
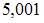
|
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| однородным относительно 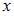 и и 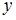 дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| ||
| линейным дифференциальным уравнением первого порядка | |||
| дифференциальным уравнением с разделяющимися переменными | |||
| уравнением Бернулли |
Тема: Дифференцирование функции комплексного переменного
Значение производной функции  в точке
в точке  равно …
равно …

| 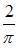
| ||

| |||

| |||

|
Тема: Комплексные числа и их представление
Главное значение аргумента комплексного числа  равно …
равно …

| 
| ||

| |||

| |||

|
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции  в точке
в точке  , вычисленное с помощью полного дифференциала, равно …
, вычисленное с помощью полного дифференциала, равно …

| 
| ||

| |||

| |||

|
Тема: Базис и размерность линейного пространства
Даны вектор  и матрица
и матрица  перехода от старого базиса к новому. Тогда координаты вектора
перехода от старого базиса к новому. Тогда координаты вектора  в новом базисе имеют вид …
в новом базисе имеют вид …

| 
| ||

| |||

| |||
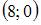
|
Тема: Поверхности второго порядка
Координаты центра поверхности 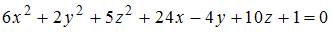 равны …
равны …

| 
| ||

| |||

| |||
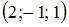
|
Тема: Типы дифференциальных уравнений
Уравнение 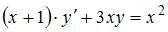 является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
однородным относительно 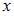 и и 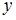 дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 
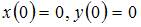 , имеет вид …
, имеет вид …

| 
| ||

| |||
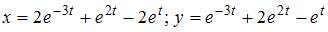
| |||

|
Тема: Полная вероятность. Формулы Байеса
Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …

| 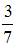
| ||

| |||
| 0,07 | |||
| 0,05 |
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины 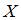 :
:

функция распределения вероятностей имеет вид:

Тогда значение параметра  может быть равно …
может быть равно …

| 0,655 | ||
| 0,25 | |||
| 0,45 |
Тема: Метрические пространства
Расстояние между матрицами  и
и  в метрике
в метрике  равно …
равно …

| |||
Тема: Гармонические колебания
Угловая частота гармонических колебаний равна  , начальная фаза
, начальная фаза  рад, а смещение колеблющейся точки от нулевого положения через 2 секунды равно 0,1. Тогда амплитуда гармонических колебаний составляет …
рад, а смещение колеблющейся точки от нулевого положения через 2 секунды равно 0,1. Тогда амплитуда гармонических колебаний составляет …

| 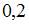
| ||

| |||

| |||

|
Тема: Элементы гармонического анализа
Разложение функции  на гармоники имеет вид …
на гармоники имеет вид …

| 
| ||

| |||

| |||

|
Тема: Периодические функции
Период функции  равен …
равен …
Дата добавления: 2015-08-17; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема: Комплексные числа и их представление 2 страница | | | Тема: Комплексные числа и их представление 4 страница |