Огляд літературних джерел за темою

Загальні відомості:

Кристал - тверде тіло з упорядкованою внутрішньою будовою, що має вигляд багатогранника з природними плоскими гранями: впорядкованість будови полягає у певній повторюваності у просторі елементів кристала (атомів, молекул, йонів), що зумовлює виникнення т.зв. кристалічної ґратки.

Кристалі́чна ґратка — геометрично правильне розміщення атомів (йонів, молекул), властиве речовині, що перебуває в кристалічномустані. Просторові фігури (наприклад, паралелепіпеди) у вершинах яких розміщено атоми, називаються комірками кристалічної ґратки, регулярна нескінченна система геометричних точок (вузлів ґратки), що є ідеально періодичною в трьох вимірах простору; існує 14 основних типів просторових ґраток.

Найменша комірка, яка зберігає усі елементи симетрії кристалу, називається елементарною коміркою.

Навіть у випадку кристалу із одним сортом атомів елементарна комірка містить кілька атомів. Наприклад, кристал заліза має кубічну об'ємноцентровану ґратку із 2 атомами в елементарній комірці. При високих температурах залізо переходить у фазу з ґранецентрованою кубічною ґраткою із 4 атомами в елементарній комірці.

Граничні умови Борна-Кармана - періодичні граничні умови, які накладаються на хвильові функції в нескінченному середовищі з трансляційною симетрією з метою дискретизації неперервного спектру одноелектронних станів.

За теоремою Блоха, хвильові функції в середовищі з трансляційною симетрією, наприклад, в нескінченному кристалі, мають вигляд

,

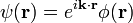де 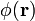- періодична функція.

При застосуванні граничних умов Борна-Кармана додатково вимагають періодичності хвильової функції з періодом 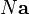, де 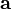- базовий вектор елементарної коміркикристала, а N - велике число. В такому випадку хвильовий вектор 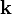може мати тільки дискретні значення (залежні від N):

,

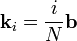де 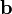- вектор оберненої ґратки. *

* Ч. Киттель. Введение в физику твердого тела. — М.: Наука, 1978.

Дата добавления: 2015-08-17