Трансверсальные цифровые фильтры

Под трансверсальными фильтрами понимают такие ЦФ, которые работают в соответствии с алгоритмом

u_i = a ₀ u_i + a ₁ u_{i -1} + a ₂ u_{i -2} + ··· + a_mu_{i - m},где а ₀, а ₁, а ₂,..., а_m — последовательность постоянных коэффициентов; т — число, определяющее порядок фильтра.

Трансверсальный фильтр производит взвешенное суммирование предшествующих отсчетов входного сигнала.

Применив z -преобразование к обеим частям уравнения (3.98), получим

V (z) = (а ₀ + а ₁ z ^-1 + а ₂ z ^-2 +... + a_mz ^{- m}) u (z).

Последнее уравнение получено с учетом теоремы о запаздывании, из которой следует, что запаздывание дискретного сигнала на один элемент соответствует умножению z -преобразование на z ^-1.

Убедимся в этом, вычисляя z -преобразование от u (i -1):

,где .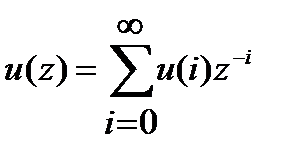

При вычислении произведена замена i -1 на m и принято во внимание, что u (-1)=0.

Отсюда системная функция

(3.99)

Частотную характеристику фильтра получаем по уравнению (3.99) заменой z = e^{j ωΔ}.

K (j ω) = а ₀ + а ₁ e ^{- j ωΔ} + а ₂ e ^{- j 2ωΔ} +... + а_me ^{- jm ωΔ}. (3.100)

Вычислим импульсную характеристику этого фильтра.

.

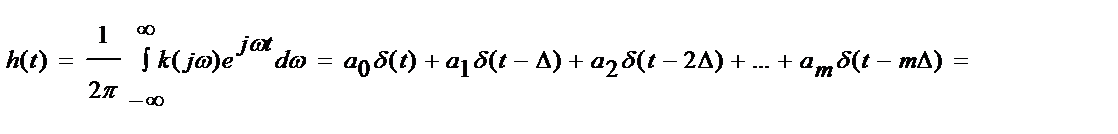
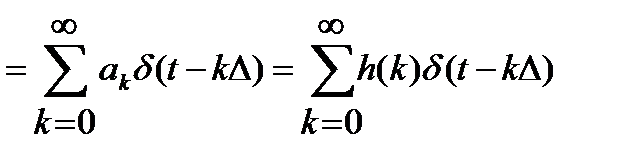Следовательно, коэффициенты a₀,a₁,…,a_m, входящие в выражения (3.98), (3.100), определяют выборочные значения импульсной характеристики.

Схема, реализующая это уравнение для m=4, приведена на рис.3.95. Она содержит идеальные линии задержки (ячейки памяти) на время, равное интервалу дискретизации Δ, перемножители и сумматор. При возбуждении трансверсального фильтра единичным импульсом

{ u_k } = (1,0,0,0....0)

и перемещения содержимого ячеек памяти путем сдвига через время дискретизации Δ на его выходе формируются выборочные значения импульсной характеристики ЦФ. При подаче на его вход совокупности выборок { u_k }, k = 0,..., т и перемещении содержимого ячеек памяти на его выходе реализуется совокупность дискретных сигналов, определяемая формулой свертки (3.91). Элементы задержки трансверсального фильтра должны обеспечивать задержку l -разрядных двоичных чисел, а перемножители и сумматоры — соответствующие математические операции с этими числами.

Дата добавления: 2015-08-20