Рекурсивный цифровой фильтр

Этот фильтр работает по следующему алгоритму: υ_i = а₀u_i + а ₁ u_{i -1} +... + a_mu_{i - m} + b ₁ υ_{i -1} + b ₂ υ_{i -2} +... + b_nυ_{i - n} , (3.101)

где а _o, а ₁,..., a_m; b ₁, b ₂,..., b_n — постоянные коэффициенты, неравные нулю.

В уравнении (3.101) участвуют выборки как входного, так и выходного сигналов.

Системная функция рекурсивного фильтра определяется выражением

Схема рекурсивного ЦФ приведена для m=4 и n=4 на рис. 3.96. Она содержит элементы задержки ( памяти), умножители и сумматор, обеспечивающий математические операции с l -разрядными двоичными числами.

При подаче на его вход совокупности выборок { u_k }, k = (0,..., m - 1) и пе­ремещения содержимого ячеек памяти,через время дискретизации Δ на его выходе формируются выборки выходного сигнала в соответствии с формулой (3.101).

46 Устойчивость фильтров. Фильтр называется устойчивым, если при любых начальных условиях реакция фильтра на любое ограниченное воздействие также ограничена. Критерием устойчивости фильтра является абсолютная сходимость отсчетов его импульсного отклика: 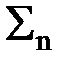|h(n)| <¥. (2.3.8)

Анализ устойчивости может быть проведен по передаточной функции. В устойчивой системе значение H(z) должно быть конечным во всех точках z-плоскости, где |z| £ 1, а, следовательно, передаточная функция не должна иметь особых точек (полюсов) на и внутри единичного круга на z-плоскости. Полюсы H(z) определяются корнями знаменателя передаточной функции (2.3.2).

Дата добавления: 2015-08-20