Пример 4.2

Вопросы к экзамену

по дисциплине «Методы оптимальных решений»

25-26 Меркулиньо

1) Метод потенциалов.

Метод потенциалов (модифицированный распределительный метод - МОДИ) является усовершенствованным вариантом распределительного метода и более практичным для решения транспортных и других задач этого типа.

Сущность метода состоит в том, что для каждой строки и каждого столбца таблицы (матрицы) определяются потенциалы (числа), с помощью которых устанавливается необходимость заполнения свободных клеток. Потенциалы определяются по заполненным клеткам. Элемент таблицы (расстояние между поставщиками и потребителями) равен сумме потенциалов строки и столбца, на пересечении которых эта клетка находится: С_ij = U_i + V_j, (2.4)

Вначале первый потенциал для строки U_i или столбца V_j принимается равным нулю, все остальные вычисляются с помощью элементов заполненных клеток:

потенциал строки U_i = C_ij - V_j, (2.5)

столбца V_j = C_ij - U_i. (2.6)

Для решения задачи методом потенциалов исходный план должен иметь число заполненных клеток m+n-1, расположенных в порядке вычеркиваемой комбинации.

Рассмотрим исходный план, полученный способом наименьшего элемента по строке, представленный в табл. 2.5. Для строки П₁ принимаем потенциал, равный 0. Затем для двух заполненных клеток определяем потенциалы столбцов: М₁ V₁ = C₁₁ – U₁ = 6 – 0 = 6,

М₂ V₂ = C₁₂ – U₁ = 5 – 0 = 5.

Таблица 2.5

Поставщик и его запас	Потребитель и его потребность	Потенциал строки Ui
М1	М2	М3	М4	М5
П1		(1)	(3)	Сijaij 8
П2		(2)		(2)	(3)		-2
П3				(1)		(3)	-1
Потенциал столбца Vj

По потенциалу столбца М₁ рассчитываем потенциал строки П₂, т.к. в ней находится заполненная клетка, имеющая потенциал в своем столбце: U₂ = С₂₁ – V₁ = 4 – 6 = -2.

Потенциал строки П₂ позволяет по двум заполненным клеткам определить потенциалы столбцов М₃ V₃ = C₂₃ – U₂ = 6 – (-2) = 8,

М₄ V₄ = C₂₄ – U₂ = 5 – (-2) = 7.

Потенциал для строки П₃ рассчитывается по заполненной клетке в столбце М₃

U₃ = С₃₃ – V₃ = 7 – 8 = -1, по которому определяется потенциал столбца М₅

V₅ = C₃₅ – U₃ = 10 – (-1) = 11.

Объем транспортной работы при этом распределении составит:

F = 1*6 + 3*5 + 2*4 +2*6 + 3*5 + 1*7 + 3*10 = 93 т-км.

Для определения оптимальности плана или необходимости его улучшения определяем сумму потенциалов строк и столбцов в свободных клетках и проставляем их в левом нижнем углу табл. 2.5.

При решении задач на минимум целевой функции F не заполняются свободные клетки, в которых сумма потенциалов С_ij меньше элемента а_ij. (на максимум – больше элемента), т.е. С_ij – (U_i + V_j) – положительна (отрицательна).

В плане (табл. 3.5) четыре клетки имеют суммы потенциалов меньше величины элементов, в двух (П₁М₃ и П₁М₄) - равны элементам и в двух (П₁М₅ и П₂М₅) больше.

Поскольку задача решается на минимум транспортной работы, то должны заполняться клетки, в которых сумма потенциалов больше элемента, при этом объем работы уменьшится на величину равную произведению характеристики клетки П₁М₅: C₁₅ – (U₁ + V₅) = 6 – 11 = -5 на записываемую в нее величину. Для этой клетки строится цепь перераспределения (рис. 2.6)

- П₁М₁ + П₁М₅

(2)

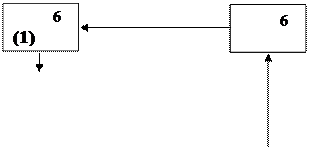
- П₂М₃ - П₁М₂ + П₁М₅

(3)

(2)

(1)

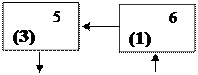
+ П₂М₁

+ П₃М₃ - П₃М₅ + П₃М_{2 -}- П₃М₅

Рис. 2.6. Рис. 2.7.

Наименьшая величина из отрицательных величин, которую можно записать в свободную клетку, равна 1, при этом целевая функция уменьшится на D = 5*1 = 5 т-км. Изменение произойдет в 5 клетках. Приняв потенциал для строки П₁ = 0, вычислим остальные потенциалы и суммы потенциалов (табл. 2.6), которые в трех клетках (П₂М₂, П₂М₅, П₃М₂) выше величины элемента.

Таблица 2.6

Поставщик и его запас	Потребитель и его потребность	Потенциал строки Ui
М1	М2	М3	М3	М4
П1			(3)			(1)
П2		(3)		(2)	(3)
П3				(1)		(2)
Потенциал столбца Vj

Наибольшую отрицательную характеристику имеет клетка П₃М₂: Н₃₂ = 6 - 9 = -3, которую нужно заполнить в первую очередь по цепи (рис. 2.7).

Таблица 2.7

Поставщик и его запас	Потребитель и его потребность	Потенциал строки Ui
М1	М2	М3	М3	М4
П1			(1)			(3)
П2		(3)		(1)	(3)
П3			(2)	(2)
Потенциал столбца Vj

В свободную клетку записывается 2, при этом объем работы уменьшится на D = 2*3 = 6 т-км. Перераспределение приведено в табл. 2.7.

После перераспределения F = 1*5 + 3*6 + 3*4 +1*6 + 3*5 + 2*6 + 2*7 = 82 т-км.

В полученном варианте плана во всех свободных клетках сумма потенциалов меньше величины элемента, следовательно, план оптимален.

Получен тот же результат, что и в распределительном методе, но метод потенциалов менее трудоемкий и более удобный для решения задач, так как на каждой итерации строится одна цепь и выполняется одно перераспределение.

Таким образом, алгоритм метода состоит из следующих этапов:

1. Cоставляется исходный допустимый план с m+n-1 заполненными клетками.

2. По элементам заполненных клеток определяют потенциалы строк U_i = C_ij - V_j и столбцов V_j = C_ij - U_i.

Первый потенциал строки или столбца принимается равным 0, остальные определяют путем вычитания из элемента заполненной клетки C_ij потенциала строки U_i или столбца V_j.

3. Для свободных клеток определяется сумма потенциалов строк и столбцов C_ij = U_i + V_j.

4. Путем сравнения суммы потенциалов с величиной элемента клетки выявляют клетку, заполнение которой приведет к улучшению плана на наибольшую величину, т.е. для которой величина С_ij - (U_i + V_j) равняется наименьшему отрицательному числу, и строят для нее цепь.

5. Проводят перераспределение цепи заполненных клеток с записью в свободную клетку наименьшей величины из отрицательных вершин цепи.

Итерационный процесс повторяется с п. 2, до получения оптимального плана перевозок, при этом на каждой итерации строится только одна цепь и связанное с ней перераспределение. Это преимущество особо заметно с увеличением размерности задачи.

Кроме рассмотренных методов решения транспортной задачи существуют методы:

- расчета планов перевозок в сетевой форме,

- условно-оптимального распределения,

- аппроксимации.

Выше рассмотренные методы решения транспортных задач использовали закрытые модели, в которых суммарные запасы поставщиков равнялись суммарным потребностям потребителей, однако на практике чаще встречаются открытые модели, в которых возможны два случая:

1) суммарные запасы поставщиков превышают суммарные потребности потребителей

,

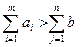2) суммарные потребности потребителей превышают суммарные запасы поставщиков

.

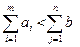В этих случаях решение транспортных задач производится путем введения дополнительных (фиктивных) поставщиков или потребителей. При этом задача открытой модели преобразуется в закрытую и решается как обычная транспортная задача.

В первом случае для сохранения баланса в матрицу вводится фиктивный потребитель, т.е. столбец, в котором отражается избыток запасов (табл. 2.8): b_n+1 = 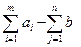= 16 – 15 = 1.

Показатели C_ij (расстояния) обычно принимаются равными нулю. При решении преобразованной задачи изложенными матричными методами клетки фиктивного потребителя заполняются не в начале (хотя C_{i j} в них минимальные), а в конце распределения. В табл. 2.8 показан оптимальный план распределения, в котором избыток запасов имеет поставщик П₃, запасы остальных поставщиков распределены полностью.

Таблица 2.8

Поставщик И его запас	Потребитель и его потребность
М1	М2	М3	М3	М4	Ф(bn+1)
П1			(1)			(3)
П2		(3)		(2)	(3)
П3			(2)	(1)			(1)

Во втором случае в матрицу вводится фиктивный поставщик, т.е. дополнительная строка, в которой отражается часть потребностей не обеспечиваемая наличными запасами с нулевыми C_ij (табл. 2.9): а_m+1 = 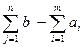= 15 – 14 = 1.

Заполнение клеток в этой строке производится после распределения имеющихся запасов между реальными потребителями. В табл. 2.9 показан оптимальный план распределения, в котором не удовлетворены потребности потребителя М₃ на 1 т.

Таблица 2.9

Поставщик И его запас	Потребитель и его потребность
М1	М2	М3	М3	М4
П1			(1)			(3)
П2		(3)		(1)	(3)
П3			(2)	(1)
Ф(аm+1)				(1)

2) Методы нахождения начального решения транспортной задачи.

Шаг 2.Транспортную таблицу начинают заполнять с левого верхнего (северо-западного) угла. При заполнении двигаются по строке вправо и по столбцу вниз. В клетку, находящуюся на пересечении первой строки и первого столбца, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: 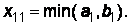Если а₁ < b₂, то х₁₁ = a₁ и предложение первого поставщика полностью исчерпано. Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, находящуюся на пересечении первого столбца и второй строки, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: х₂₁ =
= min(a ₂ ,b₁-a₁). Если b ₁ -a ₁ <a ₂то х ₂₁ = b ₁ -a ₁. Спрос первого потребителя удовлетворен. Первый столбец вычеркивают и двигаются по второй строке вправо. Заполнив клетку, стоящую на пересечении второй строки и второго столбца, переходят к заполнению следующей третьей клетки второй строки, либо второго столбца. Процесс продолжают до тех пор, пока не исчерпается предложение и не удовлетворится спрос. Последняя заполненная клетка находится в последнем n -м столбце и последней m -й строке.

Пример 4.2

Определить начальное решение по методу "северо-западного" угла для транспортной задачи из примера 4.1.

Решение.

Транспортная таблица имеет следующий вид (табл. 4.2):

Таблица 4.2

№					Предложение
	120^7	40^8	^1	^2
	^4	10^5	130 ^9	^8
	^9	^2	60 ^3	110 ^6
Спрос

В первую клетку помещают: х₁₁ = min(160,120) = 120. Спрос первого потребителя полностью удовлетворен, первый столбец вычеркивают. Остаток сырья в первом пункте составляет: 160 – 120=40 усл. ед. Двигаемся по первой строке вправо х ₂₁ =min(160 -120,50) = 40. Предложение поставщика исчерпано, первая строка вычеркивается. Второму потребителю не хватает 50-40=10 усл. ед. Двигаемся по второму столбцу вниз х ₂₂ = min(140,50 – 40) = 10; Второй столбец вычеркивается. Двигаемся по второй строке вправо х ₂₃ = min(140 -10,90) = 130. Вторая строка вычеркивается. Двигаемся по третьему столбцу вниз x₃₃ = min(170,190 -130) = 60. Спрос третьего потребителя удовлетворен. Двигаемся по третьей строке вправо х₃₄ = min(170 -160, 10) = 110. Таблица заполнена. Число ненулевых значений x_ij, 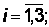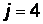, равно 6. Число базисных переменных задачи 3+4 -1=6. Остальные 3*4-6=6 переменных являются свободными, их значения равны нулю.

Начальный план перевозок имеет вид

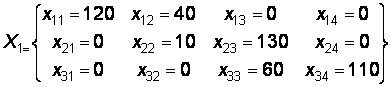
Стоимость перевозок по этому плану составляет

S₁ = 120*7+40*8+10*5+130*9+60*3+110*6=3220.

Метод "северо-западного" угла — наиболее простой метод нахождения начального решения. План перевозок, полученный по этому методу, обычно бывает достаточно далек от оптимального.

Дата добавления: 2015-08-20