Интеграция с абсолютным приоритетом.

В этом случае заявки первого класса, безусловно, снимают с обслуживания заявки второго класса при поступлении. Очевидно, что при этом вероятность блокировки для заявок первого класса никак не зависит от нагрузки второго класса и определяется только числом каналов и нагрузкой первого класса. Вероятность блокировки определяется В - формулой Эрланга

.

Определить среднее значение времени задержки для нагрузки второго класса удается аналитически только для случая N =1. Вероятность блокировки для этого случая равна

.

Нетрудно видеть, что это значение меньше, чем для вероятности блокировки в сети с интеграцией обслуживания в порядке поступления, в силу того, что отсутствует влияние заявок второго класса. Найдем теперь, какова будет задержка обслуживания для таких заявок. Построим снова диаграмму переходов состояний для модели системы с такой дисциплиной обслуживания классов заявок. Пространство состояний системы также как и в предыдущем случае будет двумерным, а структура переходов еще более сложной. На рис.5.3 приведена диаграмма состояний для интегральной сети с абсолютным приоритетом заявок первого класса. Основным отличием диаграммы переходов является наличие переходов из состояний нижнего яруса с i =0 для всех j в состояния верхнего яруса (i =1) с тем же j с интенсивностью l₁. Эти переходы отражают процесс снятия заявки второго класса с обслуживания немедленно с поступлением заявки первого класса с вероятностью равной l₁Dt в течение промежутка времени (t, t+Dt).

Рис. 5.3 Диаграмма состояний интегральной системы; абсолютный приоритет вызовам 1 – го класса; N=1 канал.

Составим уравнения равновесия для построенной модели системы. Они оказываются более сложными, чем для предыдущего случая. Выпишем сначала уравнения для нулевого состояния.

Их сразу можно разрешить относительно вероятностей состояний, соседних начальному, а затем выписать уравнения для остального множества состояний

Для решения этой системы уравнений воспользуемся методом производящих функций. Введем

Умножим (9) и (10) на z^j, и, суммируя по всем значениям j =1,2,3…,найдем после некоторых выкладок

Решая систему алгебраических уравнений и подставляя выражения (7) и (8) получим выражения для производящих функций. Далее, используя условия нормировки, выразим вероятность нулевого состояния

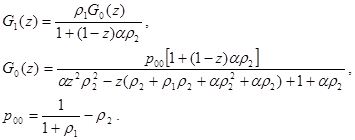
Последнее соотношение позволяет установить нетривиальное условие стабильности в системе (существования стационарного распределения вероятностей) для максимального значения коэффициента нагрузки со стороны заявок второго класса - на коммутацию пакетов

Смысл полученного неравенства состоит в необходимости обеспечения средней поступающей нагрузки второго класса меньшей, чем остаток пропускной способности канала после обслуживания нагрузки первого класса. В противном случае очередь из заявок второго класса просто переполнится и они никогда не будут обслужены (не получат доступ к каналу).

При выполнении же этого условия среднее число заявок в очереди будет конечным и может быть определено непосредственно через производящие функции по формуле

.

Воспользуемся формулой Литтла и вычислим в явном виде значение нормированного среднего времени задержки в системе для заявок второго класса

.

В качестве подтверждения правдоподобности полученного результата положим равной нулю интенсивность нагрузки первого класса. Получающееся при этом выражение будет в точности соответствовать известному выражению для задержки заявок в системе M/M/1.

Рассмотрим в качестве примера исходные данные для предыдущего раздела. При 1/ m ₁=100c,1/ m ₂=10мс, и a =10000, r ₁=0.1, r ₂=0.4 вероятность блокировки для нагрузки первого рода будет равна 0.09, что в 5 раз меньше, чем для интеграции в порядке поступления заявок. Однако при этом нормированная средняя задержка для пакетов возрастет с m₂М<T> =992 до 1600, т.е. более чем на 60%.

Можно показать, что в общем случае при достаточно больших a выигрыш в вероятности блокировки при переходе на интеграцию с абсолютным приоритетом по сравнению с обслуживанием в порядке поступления будет определяться отношением

.

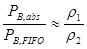В то же самое время задержка пакетов возрастет в отношении

.

Таким образом стратегия интеграции с абсолютным приоритетом, гарантируя заданное качество обслуживания для соединений, приемлема только для очень низких нагрузок со стороны передачи пакетов.

Сочетания гарантированной вероятности блокировки для соединений и минимально возможной задержки при заданной пропускной способности канала удается достигнуть, применяя адаптивное распределение ресурса - стратегию подвижной границы.

Дата добавления: 2015-08-02