Анализ времени доставки сообщений в сети с коммутацией каналов.

В качестве важного практического примера применения методов теории телетрафика рассмотрим анализ передачи данных по сети с коммутацией каналов.

Передача данных по сетям с коммутацией каналов осуществляется в три фазы - установление соединения, передача данных, разъединение соединения. Для реализации этих процессов применяется система сигнализации. На рис. 4.1 показаны упрощенно сигнальные сообщения, которыми обмениваются абоненты и коммутационные узлы в процессе передачи.

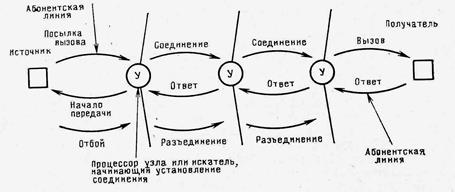
Рис. 4.1 Сигнализация в сети с коммутацией каналов.

Передача сигнализации может осуществляться как по специальному общему для всех коммутируемых каналов каналу сигнализации (ОКС), так и в полосе речевого сигнала, т.е. по тем же соединительным линиям, по которым передаются информационные сообщения. Рассмотрим сначала именно этот случай. Найдем время установления соединения, которое будет являться функцией нагрузки в сети, длины управляющих и информационных сообщений, интенсивности передачи сигнальных сообщений и данных (скорости передачи), а также числа каналов (соединительных линий) предоставленных для связи. Рассмотрим модель сети с коммутацией каналов в виде системы обслуживания, в которой вызовы ожидают освобождения каналов, а не блокируются. Отбросим на этом этапе проблему маршрутизации, предположив сеть полносвязной. На рис. 4.2 показана модель СМО, соответствующая сделанным предположениям. Два узла коммутации А и В связаны между собой N каналами (СЛ) с пропускной способностью С_L,бит/с. Пусть это также и скорость передачи по абонентскому шлейфу. С этой скоростью данные будут передаваться по каналу после установления соединения. Вызовы от абонентских устройств поступают на узел А и находятся в очереди пока не станет свободным хотя бы одна СЛ до узла В. На рис. 4.3 показаны все составляющие времени Т_с –времени установления соединения от момента передачи сообщения запроса передачи до момента приема сообщения о начале передачи. Временем на соединение узла В и получателя пренебрегаем. Показанные отрезки времени требуется для передачи каждого из сигнальных сообщений, обработка в узлах А и В требует в каждом случае среднее время M< Т_р>. Среднее время ожидания в очереди в узле А до освобождения одного из N каналов обозначено M<W>.

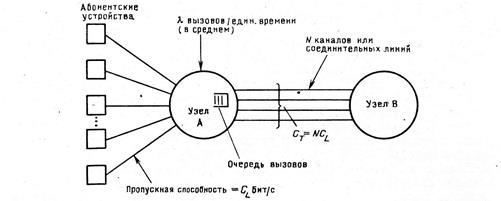
Рис. 4.2 Пара узлов в полносвязной сети с коммутацией каналов; модель системы обслуживания; сигнализация по разговорному каналу.

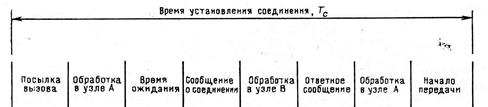
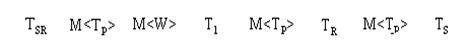
Рис. 4.3 Составляющие времени установления соединения.

Теперь примем для простоты, что каждое сигнальное сообщение имеет одну и ту же длину и требует времени передачи Т_s. Время передачи сообщения о соединении примем равным Т_I. При таком упрощении время соединения равно:

.

Для расчета среднего времени ожидания M<W> воспользуемся моделью системы обслуживания типа M/M/N с бесконечной длиной буфера и N серверами. Предположение о пуассоновском распределении потока вызовов является, как правило, адекватным в задачах со многими абонентами, допущение о показательном распределении времени обслуживания существенно более грубое, однако описание времени обслуживания статистикой общего вида сильно усложнит задачу.

Пусть интенсивность потока вызовов в узел А равна λ, а среднее значение времени обслуживания – 1/ μ. Тогда можно использовать модель M/M/N со следующими характеристиками интенсивностей переходов

Здесь n - состояние СМО, т.е. число установленных соединений, включая обслуживаемый вызов. Решение уравнений равновесия для данной системы было дано ранее. Введя параметр ρ=λ/(μN), стационарные вероятности состояний определяются как

Теперь можно определить все необходимые характеристики качества обслуживания. Найдем сначала вероятность того, что сообщение будет задержано в системе, т.е. заявка не найдет свободного сервера. Очевидно, что эта вероятность равна

.

Мы ранее получали эту формулу в несколько ином виде (явно выписывая вероятность p₀). Эта формула известна как С - формула Эрланга: .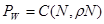

Обратите внимание, что вторым аргументом в С - формуле Эрланга используется полная нагрузка на пучок каналов, а не удельная нагрузка ρ <1. Будем для определенности обозначать далее полную нагрузку A=ρN. Эта нагрузка, конечно, также измеряется в Эрлангах.

Рассмотрим пример.

Пусть нагрузка на узел λ/μ =0.8 Эрл и в одном случае узел имеет один исходящий канал N =1, а в другом – пять (N =5). Вычислим С(1,0.8)=0.8 и С(5.0.8)=0.0018. Таким образом, применение пяти каналов вместо одного сокращает вероятность задержки более чем в 400 раз.

Найдем теперь среднее число сообщений, ожидающих обслуживание. Оно равно разности между средним числом сообщений в системе и средним числом сообщений, находящихся на обслуживании

.

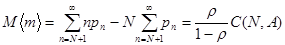В качестве подтверждения правильности сделанного вывода можно найти значение среднего числа ожидающих сообщений для N=1. Оно получится в точности таким, как было выведено ранее для СМО типа M/M/1.

.

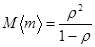Теперь найдем среднее число сообщений, находящихся в системе M<n> и число сообщений, находящихся в обслуживании M<s>. Вычисление показывает, что

Пользуясь формулой Литтла теперь можно найти задержку в узле M< T> и среднее время ожидания для сообщения М< W>:

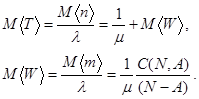
Для иллюстрации вернемся к рассмотренному ранее примеру. Пусть А =0.8 Эрл. При N =1 получим, что среднее время ожидания составит M<W>=1/μ (0.8/0.2)=4(1/μ), а средняя задержка M<T>=5(1/μ). При среднем времени занятия канала 1/μ =0.1c получим M<W>= 0.4c, M<T>= 0.5c. Если теперь увеличить число исходящих каналов до пяти, то при тех же предположениях будем иметь M <W>= 0.0004(1/μ) = 40 мс. Таким образом, применение многоканальной системы резко снижает время ожидания обслуживания.

С другой стороны интересен вопрос о целесообразности разделения одного канала фиксированной пропускной способности на несколько менее производительных каналов.

Пусть имеется канал с пропускной способностью 9600 бит/c и нужно решить, стоит ли разделить его на 5 отдельных каналов по 1920 бит/с. Предположим, что 1 /μ =10 мс, т.е. сообщения имеют среднюю длину 192 бита. Средняя задержка при нагрузке А =0.8 при пяти каналах будет равна:

M<W> =10^-2C(5,0.8)/(5-0.8)= 0,1 сек

Если же использовать один канал со скоростью передачи 9600 бит/с, значение среднего времени ожидания будет равно:

M<W> =0,024сек

Что существенно меньше. Таким образом, канал с большей пропускной способностью предпочтительнее, чем составляющие его каналы с меньшей пропускной способностью для передачи некоторого заданного объема пакетов данных.

В случае передачи сообщений по сети с коммутацией каналов собственно время передачи данных Т_М представляет собой только одну из составляющих и для определения величины среднего времени обслуживания 1/μ необходимо учитывать все составляющие времени занятия канала. Обозначим далее среднее значение этого полного времени занятия канала

T_н=1/μ=4T_s+T_I+4M<T_p>+T_M

Эта формула соответствует временной диаграмме занятия канала, изображенной на рис.4.4 в предположении, что все сигнальные сообщения имеют одну и ту же длительность T_s.

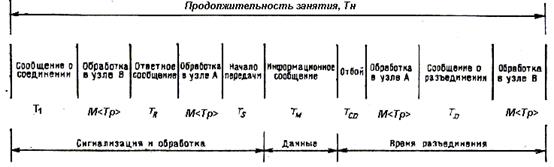
Рис. 4.4 Составляющие времени занятия; пример рис. 2.

С уже сделанной оговоркой о предположении экспоненциальности распределения этого времени (из формулы видно, что это сумма случайных величин), будем использовать полученное ранее соотношение для расчета среднего времени ожидания обслуживания

Введем величину, определяющую параметр удельного полезного использования канала ρ_M=λT_M/N. Этот параметр отличается от обычного коэффициента использования ρ=λT_H/N, который не различает время на передачу информационного сообщения и время на передачу сигнализационных сообщений.

Рассмотрим зависимость нормированного времени установления соединения в сети с коммутацией каналов T_C /T_M от параметра удельного полезного использования канала при различных длительностях передачи сигнальной информации. Примем для определенности время передачи сообщения о соединении T _I=0.1 T_M. Обозначим T_sig – время для передачи всех других сигнальных сообщений (4 T_s). Пусть узел имеет N =10 исходящих каналов. На рисунке 4.5. приведены два графика, позволяющие проанализировать некоторые характерные черты сети с коммутацией каналов. Графики построены для двух случаев – когда время для передачи сигнальных сообщений T_sig различаются в десять раз. Как видно из графиков, такое различие приводит к разным предельным значениям параметра полезного использования канала от 0.67 до 0.88 при меньших в десять раз длительностях сигнальных пакетов. Также видно, что увеличение нагрузки на узел сначала медленно, а затем резко увеличивает время установление соединения, причем сокращение сигнальных сообщений в любом случае уменьшает это время.

Рисунок 4.5. Нормированное время распределения соединения; N = 10 каналов T₁=0.1T_M

Дата добавления: 2015-08-02