Интеграция на основе стратегии подвижной границы.

При этом методе интеграции N канальных интервалов делятся на две части. Одна часть, содержащая N₁ канальных интервалов, предназначается для обслуживания нагрузки первого класса (запросов на соединение). Другая часть, содержащая N₂=N-N₁ канальных интервалов, резервируется для пакетов – обслуживания нагрузки второго класса. Пакеты могут занимать также любой из N₁ канальных интервалов первого класса, если он не используется в данный момент времени. Однако при поступлении заявки первого класса она имеет абсолютный приоритет перед нагрузкой второго класса и сбрасывает при необходимости пакет, занимающий один из N₁ канальных интервалов. В этом и состоит смысл подвижной границы между группами каналов, отведенных для двух различных классов нагрузки. На рис. 5.4 приведена иллюстрация этого метода.

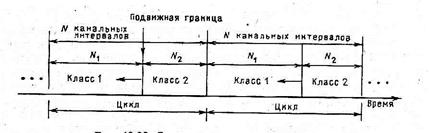
Рис. 5.4 Стратегия подвижной границы.

Очевидно, что вероятность блокировки для нагрузки первого класса при такой стратегии предоставления ресурса определяется по В - формуле Эрланга для N₁ серверов. Задержка для пакетов при этом будет не хуже, чем рассчитанная для системы с N ₂ серверами, а лучше, поскольку вся оставшаяся от обслуживания нагрузки первого класса пропускная способность системы будет также использоваться для обслуживания пакетов. В системе такого типа также может возникнуть перегрузка для нагрузки второго класса. Максимально допустимая величина этой нагрузки не должна превышать

.

Здесь вероятность блокировки для нагрузки первого класса определяется по В - формуле Эрланга. Записанное соотношение может быть интерпретировано как интуитивно очевидное, поскольку выражает собой условие не превышать единицу для среднего на один сервер коэффициента использования по отношению к нагрузке второго класса

.

В знаменателе при этом находится выражение описывающее среднее число каналов, доступных для очереди пакетов. С другой стороны, оно может быть переписано в виде условия ограничения величиной N полной средней нагрузки на систему

.

Общий анализ системы с подвижной границей оказывается слишком сложным с алгебраической точки зрения. Поэтому при аналитическом исследовании применяются приближенные методы. Раздельно изучаются два возможных режима – не перегруженный (ρ₂<N₂) и режим перегрузки при нарушении этого неравенства. Мы далее построим точное решение задачи с подвижной границей, но только для случая, когда N =2. При этом для реализации стратегии существует единственная возможность выделения под нагрузку первого класса N₁ =1 один канальный интервал. Тогда пакеты будут получать один канальный интервал в любом случае, и два, если заявка на соединение будет отсутствовать. Поступление такой заявки немедленно будет снимать один из пакетов с обслуживания, и ставить в общую очередь из заявок второго класса.

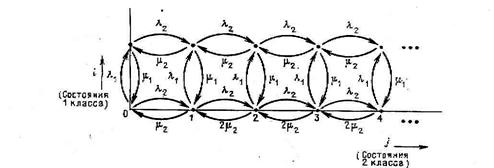
Рис. 5.5 Диаграмма состояний системы с подвижной границей; N=2 канала; N₁=N₂=1 канал.

Рассмотрим диаграмму состояний для такой системы (Рис. 5.5). Пространство состояний для нее также двумерное и состояния могут быть разделены на два яруса, соответствующих случаям i =0 - соединение не установлено и i =1 соединение установлено. В последнем случае диаграмма состояний полностью соответствует системе M/M/1, поскольку один канальный интервал из двух занят под нагрузку первого класса, а второй используется как обычная система с ожиданием. При i =0 имеем диаграмму, соответствующую модели M/M/2, поскольку в случае, когда отсутствует нагрузка первого класса все канальные интервалы (а их у нас два) обслуживают пакетную нагрузку. Переходы между ярусами происходят при поступлении заявки на соединение с интенсивностью l ₁, которое переключает систему обслуживания пакетов с двухлинейной на однолинейную, или при завершении соединения с интенсивностью m ₁, которое производит обратное переключение. Выпишем пять уравнений равновесия для рассматриваемой системы.

Для нахождения решения построенной системы уравнений требуется еще два уравнения. Одно из них это условие нормировки всех вероятностей, а в качестве еще одного будет использовано свойство корней многочлена знаменателя одной из производящих функций.

Определим две производящие функции

Умножая почленно уравнение (11) на z^j и суммируя по всем значениям j >0, преобразуем это уравнение в алгебраическое относительно производящих функций. Повторяя ту же процедуру с уравнением (12) и исключая неизвестные составляющие с помощью (13), (14). Получим в итоге:

Полученные уравнения позволяют сразу выписать несколько важных соотношений, приводящих к определению вероятности блокировки нагрузки первого класса:

Это соотношение в точности соответствует В-формуле Эрланга для однолинейной системы.

Теперь перейдем к определению среднего времени задержки пакетов. Складывая уравнения для производящих функций, сокращая общий множитель правой и левой частях (1-z) и обозначив отношение l₂/m₂=r₂, найдем следующее соотношение

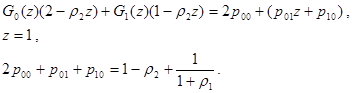
Введем несколько обозначений

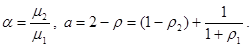
Тогда можно найти в явном виде выражения для вероятностей

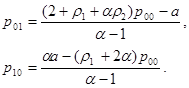
Выпишем теперь выражения для производящих функций

Найдем соотношение для среднего числа пакетов в системе, исходя из формулы для производящих функций

В качестве подтверждающих правдоподобность полученного выражения соотношений найдем предел правой части при стремлении к нулю нагрузки первого класса и предел при стремлении этой нагрузки к бесконечности.

В первом случае результат в точности соответствует модели M/M/2, а во втором - модели M/M/1, что и соответствует нашим представлениям.

Воспользовавшись формулой Литтла, выпишем выражение для нормированной задержки в системе

.

Это выражение еще не является окончательным, поскольку содержит три вероятности, связанные только двумя уравнениями. Как уже было отмечено, воспользуемся некоторыми свойствами корней знаменателя выражения для производящей функции G₀(z). Обратимся к выписанному выше выражению для этой функции.

Пусть z₀ - корень многочлена D ₀. Из определения производящей функции необходимо выполнение требования

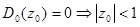
При этом значении z выражение для числителя также должно обратиться в ноль. Полученное при этом выражение N₀(z₀)=0 и определяет третье необходимое уравнение для нахождения всех вероятностей, входящих в выражение для задержки. Решение алгебраического уравнения третьей степени в общем случае не дается в виде конечной формулы. Мы используем приближенное решение этого уравнения для нахождения двух различных формул для определения задержки пакетов в системе с подвижной границей

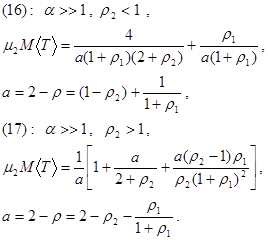
На рис.5.6 приведены графики функции нормированной задержки при различных значениях нагрузки первого класса. Для сравнения приведен график задержки для системы с фиксированным разделением каналов для двух классов нагрузки (по одному каналу на каждый). Как видно из сравнения стратегия подвижной нагрузки дает существенный выигрыш в характеристиках качества обслуживания по сравнению с другими способами интеграции каналов. Анализ показывает, что такое преимущество только усиливается при увеличении числа канальных ресурсов.

Рис.5.6 Сравнение систем с подвижной и фиксированной границей; N=2; N₁=N₂=1.

6 Система типа G/G/1.

Как следует из определения, этот класс систем предполагает, что как распределение интервалов времени между поступлением входных заявок-требований, так и распределение времени обслуживания в сервере описываются произвольными функциями плотности вероятности. Обозначим функцию плотности вероятности входного потока заявок a(t), а функцию плотности вероятности времени обслуживания b(x). Рассмотрим последовательность поступающих заявок на обслуживание - требований, пронумерованных индексами и вспомним обозначения, введенные ранее.

C_n - n -е требование, поступающее в систему,

t_n - промежуток времени между поступлениями n -го и n -1 требований, плотность вероятности a(t) - не зависит от n.

x_n - время обслуживания n -го требования, плотность вероятности b(x) -также не зависит от n,

w_n - время ожидания n - го требования в очереди.

Напомним определение незавершенной работы для системы массового обслуживания. По определению незавершенная работа в каждый момент времени - это остаточное время, необходимое для освобождения системы от всех требований, находящихся в ней к этому моменту. Очевидно, что для системы G/G/1 значение незавершенной работы непосредственно перед поступлением n-го требования в точности равно времени w_n. Таким образом, последовательность этих значений будет образовывать дискретную марковскую цепь, вероятности переходов которой могут быть определены по характеристикам входного потока и времени обслуживания. Зная эти переходные вероятности можно найти все характеристики изучаемой СМО. Рассмотрим два случая поступления требования С_n в систему - поступление в занятую систему (Рис. 6.1) и в свободную систему (Рис. 6.2).

Рис. 6.1 Случай, когда требование C_n+1 поступает в занятую систему.

Рис. 6.2 Случай, когда требование C_n+1 поступает в свободную систему.

Нетрудно видеть, что для первого случая

.

Для второго случая .

Определим случайную величину, равную разности между временем обслуживания требования с номером n и промежутком времени между поступлениями n +1 и n -го требований .

Фундаментальное свойство этой случайной величины состоит в том, что для стабильных СМО, т.е. имеющих стационарное распределение вероятностей состояний, ее математическое ожидание должно быть отрицательным. Смысл этого утверждения понятен из определения. Очевидно, что в среднем время обслуживания должно быть меньше времени между поступлениями соседних требований. Используя эту величину можно записать выражение для рекуррентного определения величин w_n в компактном виде

Решая это уравнение последовательно, начиная с нулевого требования, можно получить

.

Условие стабильности М<u_n> <0, может быть записано в более привычной форме:

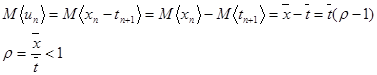
При выполнении этого условия будет существовать стационарное распределение вероятностей

Эта функция распределения может быть записана через искомую плотность вероятности для времени ожидания в очереди

.

Для ее нахождения Линдли получил интегральное уравнение, носящее его имя.

Функция c(u) определяется в свою очередь интегралом, похожим на свертку плотностей вероятности входного потока заявок и времени обслуживания

.

Решить уравнение Линдли в общем случае не удается. Если ввести преобразования Лапласа от функций плотности вероятности

то удается записать:

Определение функции комплексной переменной W(s) из последнего уравнения согласно методам теории функций комплексной переменной сводится к представлению разности в квадратных скобках в виде отношения функций комплексной переменной, имеющих специальное расположение нулей в правой и левой полуплоскости комплексной переменной s:

.

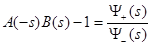При Re(s)> 0 функция в числителе должна быть аналитической и не иметь нулей в этой полуплоскости. Функция в знаменателе должна быть аналитической в левой полуплоскости и не иметь там нулей. Решение для преобразования Лапласа функции плотности вероятности времени ожидания в очереди может быть записано в виде

Константа K есть вероятность того, что требование не будет стоять в очереди. Вычисления показывают, что, несмотря на то, что приведенный подход позволяет выразить функцию плотности вероятности времени ожидания в любом конкретном случае заданных плотностей a(t) и b(x), записать в общем случае решение для характеристик качества обслуживания системы G/G/1 не удается. Так для среднего времени ожидания требования в очереди удается получить формулу только в виде, содержащем некоторые неизвестные параметры

.

Здесь известные параметры s_a, s_b - среднеквадратичные отклонения для входного потока требований и времени обслуживания, - среднее значение интервала времени между входными требованиями. Последнее слагаемое есть отношение второго момента к среднему значению случайной величины I - продолжительности свободного состояния в системе G/G/1. Это слагаемое не определяется в явном виде и формула для M<W> не позволяет непосредственно вычислить среднюю задержку в системе.

Найдем приближенное значение этой величины при больших значениях нагрузки. Используем разложение функций комплексной переменной A(s) и B(s) в ряд Маклорена:

Поскольку нас интересует значение функции плотности вероятности при большой нагрузке, можно ограничиться рассмотрением функции W(s) при малых значениях s. Нетрудно видеть, что последнее выражение как функция комплексной переменной имеет два нуля. Первый из них очевиден: s₁ =0. Для нахождения второго корня будем пренебрегать квадратом разности между средним временем обслуживания и среднем интервалом между поступлениями. Приближенное значение корня будет равно

.

Таким образом, в качестве приближения в окрестности нуля можно считать

Как видно приближение при большой нагрузке позволяет считать распределение времени ожидания в очереди экспоненциальным, а среднее время рассчитывать по полученной выше формуле.

Кроме полученной здесь формулы для больших значений r, во многих случаях более точные результаты могут быть найдены с использованием верхней и нижней границы для времени ожидания, без предположения о величине нагрузки. Строгое значение для верхней границы можно найти, используя полученную выше формулу для M<W>. Путем простых преобразований нетрудно показать, что для любых значений нагрузки будет выполняться неравенство

.

Можно видеть, что верхняя граничная оценка оказывается тем более точной, чем больше величина нагрузки. Другими исследователями (Marchall) была получена другая формула для верхней границы. При ее выводе автор исходил из требования превращения оценки в точное выражение для задержки в системе M/G/1 при подстановке в формулу соотношений, справедливых для пуассоновского входного потока.

Последний параметр носит название коэффициента изменчивости времени обслуживания.

Нахождение нижней границы проще всего выполняется в предположении, что входной поток может быть отнесен к классу случайных потоков событий с монотонным возрастанием интенсивности. Для таких классов случайных потоков функция распределения удовлетворяет соотношению

В этом случае нижняя граница для среднего времени ожидания требования в очереди может быть определена следующей формулой

.

В более общем случае нахождение нижней границы дается через решение нелинейного уравнения:

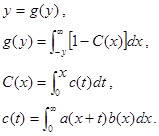
Графически решение нелинейного уравнения y = g(y) дается точкой пересечения (см. Рис. 6.3) прямой Y = y и Y = g(y). Это решение и определяет собой величину точной нижней границы для среднего значения времени ожидания требования в очереди W_Low

.

Рис. 6.3 Определение нижней границы W_M.

Итак, анализ СМО G/G/1, в которой учитывается вид функции плотности вероятности как входного потока заявок так и времени обслуживания, позволяет в ряде случаев получить некоторые оценки, которые могут быть использованы как более точные по сравнению с максимально высокими, получаемыми при использовании марковских моделей.

Дата добавления: 2015-08-02