
Читайте также:
|
1. Освободим балку от заделки. Известно, что со стороны заделки на балку действуют реактивные силы и пара сил. Реактивную силу представим в виде трех составляющих ROX, ROY, ROZ (рис. 4.16, б), действующих вдоль осей координат, а реактивный момент - в виде моментов пар MOX, MOY, MOZ, действующих в плоскостях, перпендикулярных осям (эти моменты изображены на рис. 4.16, б круговыми стрелками, огибающими оси против хода стрелки часов, если смотреть со стороны положительного направления оси).
2. Равномерно распределенную нагрузку заменим сосредоточенной силой:
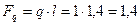 кН.
кН.
3. Составим уравнения равновесия:
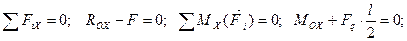
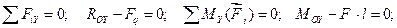
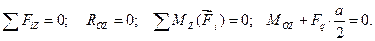
4. Решая уравнения, находим:
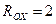 кН;
кН; 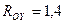 кН;
кН; 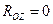 ;
;
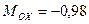 кН×м;
кН×м; 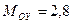 кН×м;
кН×м; 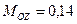 кН×м.
кН×м.
5. По найденным модулям составляющих реактивной силы RO и момента реактивной пары MO (они показаны на рис. 4.16, в раздельно) можно определить их модули RO и MO и направление действия.
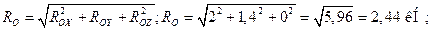
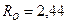 кН;
кН;
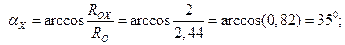
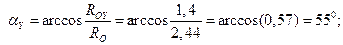
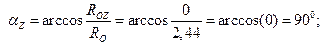
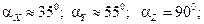
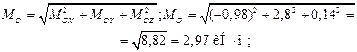
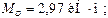
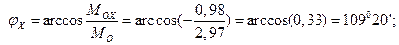
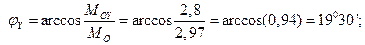
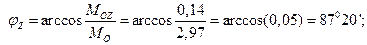
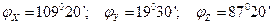 .
.
Ответ: 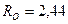 кН;
кН; 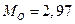 кН.
кН.
Пример 108. На валу жестко закреплены шестерня 1 и колесо 2 (рис. 4.17, а). Определить в положении равновесия вала реакции подшипников А и В, а также силы F 2 и 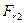 = 0,4 F 2, действующие на колесо, если F 1 = 400 Н, а
= 0,4 F 2, действующие на колесо, если F 1 = 400 Н, а 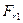 = 0,4 F 1. Силой тяжести вала, шестерни и колеса пренебречь.
= 0,4 F 1. Силой тяжести вала, шестерни и колеса пренебречь.
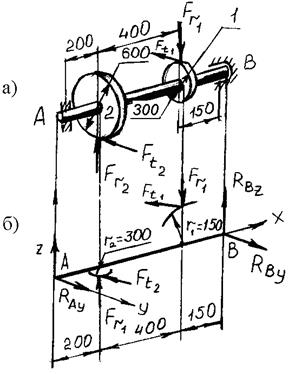
Рис. 4.17. К примеру 108
Решение. Отбрасываем связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие 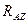 ,
, 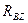 ,
,  ,
, 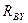 . Выбираем пространственную систему координат так, чтобы ось X располагалась по оси вала, ось Y – параллельно силам
. Выбираем пространственную систему координат так, чтобы ось X располагалась по оси вала, ось Y – параллельно силам 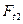 и
и 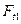 и ось Z – силам
и ось Z – силам 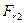 и
и 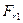 . В точках А и В будут приложены реакции связей: в точке А -
. В точках А и В будут приложены реакции связей: в точке А - 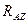 и
и 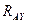 , а в точке В -
, а в точке В - 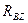 и
и 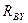 (рис. 4.17, б).
(рис. 4.17, б).
Составляем уравнения равновесия сил, произвольно расположенных в пространстве:
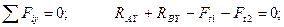 (4.48)
(4.48)
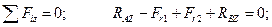 (4.49)
(4.49)
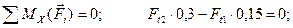 (4.50)
(4.50)
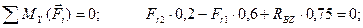 (4.51)
(4.51)
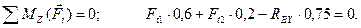 (4.52)
(4.52)
Из уравнения (4.50)
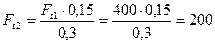 Н.
Н.
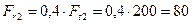 Н.
Н.
Из уравнения (4.52)
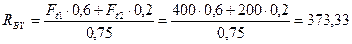 Н.
Н.
Из уравнения (4.51)
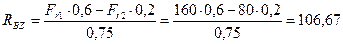 Н.
Н.
Из уравнений (4.48) и (4.49):
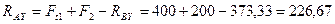 Н;
Н;
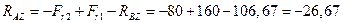 Н.
Н.
Следует отметить, что уравнение 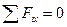 даст тождество 0 = 0.
даст тождество 0 = 0.
Полная реакция опоры А
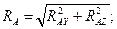
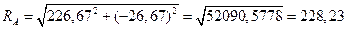 Н.
Н.
Полная реакция опоры В
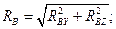
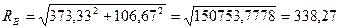 Н.
Н.
Ответ: 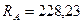 Н;
Н; 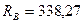 Н.
Н.
Пример 109. На валу жёстко закреплены шестерня 1 и колесо 2. Определить в положении равновесия вала реакции подшипников А и В, а также силы 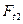 и
и 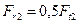 , действующие на колесо, если
, действующие на колесо, если 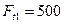 Н, а
Н, а 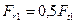 . Силой тяжести вала, шестерни и колеса пренебречь.
. Силой тяжести вала, шестерни и колеса пренебречь.

Рис. 4.18. К примеру 109
Решение. Освобождаем вал от связей (подшипников) в точках А и В, заменим связи реакциями связей. Выбираем пространственную систему координат с началом в точке А, чтобы ось X располагалась по оси вала, ось Y – параллельно силам 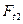 и
и 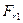 и ось Z – параллельно силам
и ось Z – параллельно силам 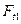 и
и 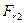 . В точках А и В будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках, а именно: в точке А -
. В точках А и В будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках, а именно: в точке А - 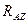 и
и 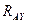 , а в точке В -
, а в точке В - 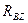 и
и 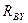 (рис. 4.18, б).
(рис. 4.18, б).
Составляем уравнения равновесия сил, произвольно расположенных в пространстве:
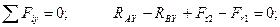 (4.53)
(4.53)
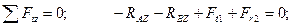 (4.54)
(4.54)
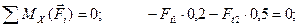 (4.55)
(4.55)
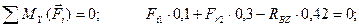 (4.56)
(4.56)
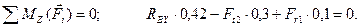 (4.57)
(4.57)
Из уравнения (4.55)
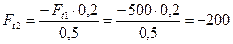 Н.
Н.
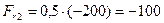 Н.
Н.
Из уравнения (4.56)
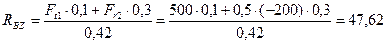 Н.
Н.
Из уравнения (4.57)
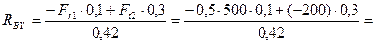
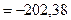 Н.
Н.
Из уравнения (4.53)
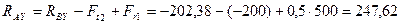 Н.
Н.
Из уравнения (4.54)
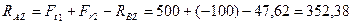 Н.
Н.
Следует отметить, что уравнение 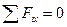 даст тождество 0 = 0.
даст тождество 0 = 0.
Полная реакция опоры А
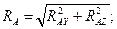
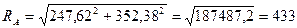 Н.
Н.
Полная реакция опоры В
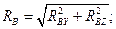
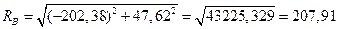 Н.
Н.
Ответ: 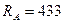 Н;
Н; 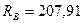 Н.
Н.
Пример 110. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 4.19, а? Определить также реакции подшипников А и В.
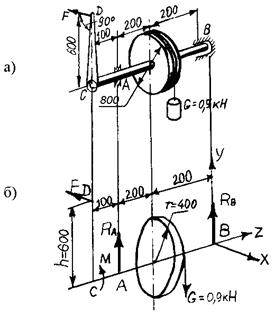
Рис. 4.19. К примеру 110
Решение. На вал действуют сила тяжести груза G, реакции опор 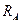 ,
, 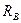 и пара сил с моментом М на рукоятке (рис. 4.19, б). Выберем систему координат и составим уравнение равновесия вала
и пара сил с моментом М на рукоятке (рис. 4.19, б). Выберем систему координат и составим уравнение равновесия вала
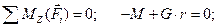
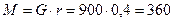 Н×м.
Н×м.
Сила на рукоятке
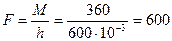 Н.
Н.
Определим реакции опор 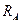 и
и 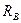 :
:
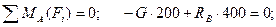
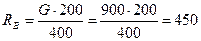 Н.
Н.
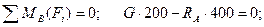
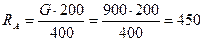 Н.
Н.
Ответ: 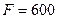 Н;
Н; 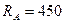 Н;
Н; 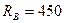 Н.
Н.
Пример 111. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 4.20, а? Определить также реакции подшипников А и В.
Решение. На вал действуют сила тяжести груза G, реакции опор 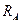 ,
, 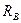 и пара сил с моментом М на рукоятке (рис. 4.20, б). Выберем систему координат и составим уравнения равновесия вала:
и пара сил с моментом М на рукоятке (рис. 4.20, б). Выберем систему координат и составим уравнения равновесия вала:
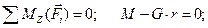
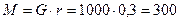 Н×м.
Н×м.
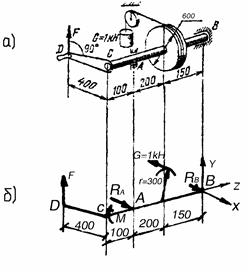
Рис. 4.20. К примеру 111
Если принять длину рукояти 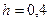 м, то сила на рукоятке
м, то сила на рукоятке
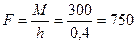 Н.
Н.
Определим реакции опор 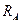 и
и 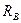 :
:
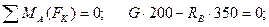
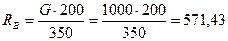 Н.
Н.
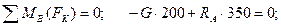
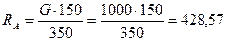 Н.
Н.
Ответ: 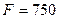 Н;
Н; 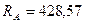 Н;
Н; 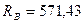 Н.
Н.
Пример 112. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 4.21, а? Определить также реакции подшипников А и В.
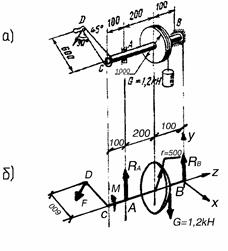
Рис. 4.21. К примеру 112
Решение. На вал действуют сила тяжести груза G, реакции опор 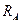 ,
, 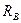 и пара сил с моментом М на рукоятке (рис. 4.21, б). Выберем систему координат и составим уравнения равновесия вала:
и пара сил с моментом М на рукоятке (рис. 4.21, б). Выберем систему координат и составим уравнения равновесия вала:
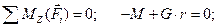
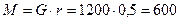 Н×м.
Н×м.
Если принять длину рукояти 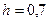 м, то сила на рукоятке
м, то сила на рукоятке
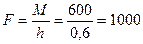 Н.
Н.
Определим реакции опор:
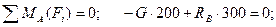
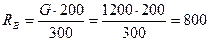 Н.
Н.
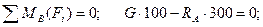
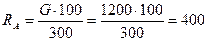 Н.
Н.
Ответ: 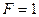 кН;
кН; 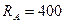 Н;
Н; 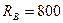 Н.
Н.
Пример 113. Однородная квадратная крышка ABCD люка может вращаться вокруг оси, проходящей через петли А и В. Горизонтальная веревка DE удерживает крышку в равновесии в положении, показанном на рис. 4.22, а. Определить реакции опор А и В, если сила тяжести крышки G = 48 H.
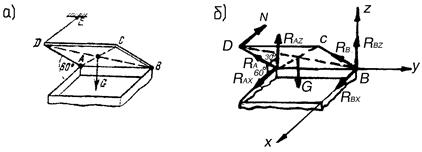 |
Рис. 4.22. К примеру 113
Решение. Внешние связи для пластины – шарниры в точках А, В и нить. Заменим их реакциями связей. Реакции петель А и В представим в виде двух составляющих 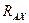 ,
, 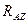 и
и 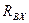 ,
, 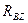 соответственно, а реакцию нити N направим вдоль линии DE (рис. 4.22, б).
соответственно, а реакцию нити N направим вдоль линии DE (рис. 4.22, б).
Уравнения равновесия:
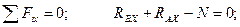 (4.58)
(4.58)
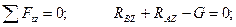 (4.59)
(4.59)
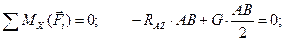 (4.60)
(4.60)
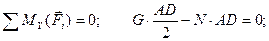 (4.61)
(4.61)
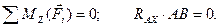 (4.62)
(4.62)
Из уравнения (4.62) системы
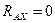 .
.
Из уравнения (4.61)
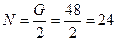 Н.
Н.
Из уравнения (4.58)
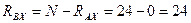 Н.
Н.
Из уравнения (4.60)
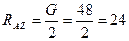 Н.
Н.
Из уравнения (4.59)
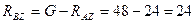 Н.
Н.
Полная реакция шарнира В
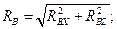
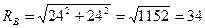 Н.
Н.
Ответ: 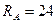 Н;
Н; 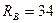 Н.
Н.
Пример 114. Полка, нагруженная, как показано на рис. 4.23, а, силой тяжести G = 0,8 кH и могущая вращаться около оси, проходящей через петли А и В, удерживается в равновесии в горизонтальном положении стержнем DC, образующим с вертикалью угол 60°. Определить реакции петель А, В и стержня DC.
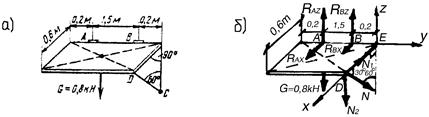
Рис. 4.23. К примеру 114
Решение. Внешние связи для пластины – шарниры в точках А, В и стержень. Заменим их реакциями связей. Реакции петель А и В представим в виде двух составляющих 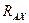 ,
, 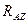 и
и 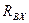 ,
, 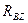 соответственно, а реакцию стержня N направим вдоль линии DС (рис. 4.23, б).
соответственно, а реакцию стержня N направим вдоль линии DС (рис. 4.23, б).
Для составления уравнений равновесия силу N удобно разложить на две составляющие, одна из которых, 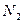 , параллельна оси Z, другая,
, параллельна оси Z, другая, 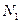 , расположена в плоскости XOY параллельно оси X. При этом
, расположена в плоскости XOY параллельно оси X. При этом 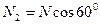 ,
, 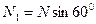 .
.
Уравнения равновесия:
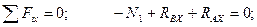 (4.63)
(4.63)
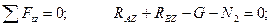 (4.64)
(4.64)
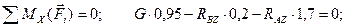 (4.65)
(4.65)
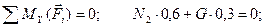 (4.66)
(4.66)
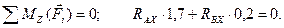 (4.67)
(4.67)
Из уравнения (4.66)
 Н.
Н.
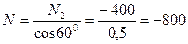 Н.
Н.
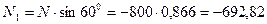 Н.
Н.
Из уравнений (4.63) и (4.67) следует:
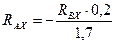 ;
;
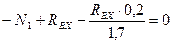 ;
; 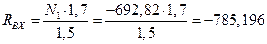 Н;
Н;
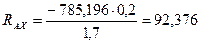 Н.
Н.
Из уравнений (4.64) и (4.65) следует:
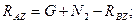
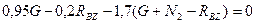 ;
;
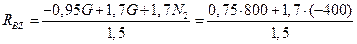
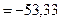 Н
Н
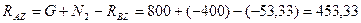 Н.
Н.
Полная реакция петли А
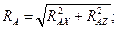
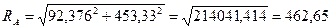 Н.
Н.
Полная реакция петли В
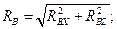
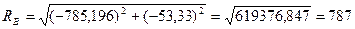 Н.
Н.
Ответ: 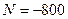 Н;
Н; 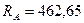 Н;
Н; 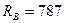 Н.
Н.
Пример 115. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 4.24, a. Определить силы 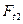 и
и 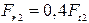 , а также реакции опор А и В, если F 1 = 120 H.
, а также реакции опор А и В, если F 1 = 120 H.
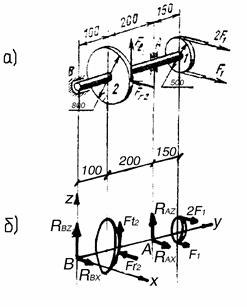
Рис. 4.24. К примеру 115
Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие 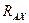 ,
, 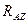 и
и 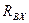 ,
, 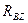 (рис. 4.24, б).
(рис. 4.24, б).
Составляем уравнения равновесия сил, произвольно расположенных в пространстве:
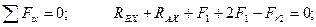 (4.68)
(4.68)
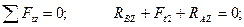 (4.69)
(4.69)
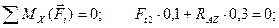 (4.70)
(4.70)
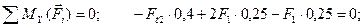 (4.71)
(4.71)
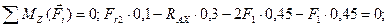 (4.72)
(4.72)
Из уравнения (4.71)
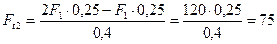 Н.
Н.
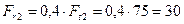 Н.
Н.
Из уравнения (4.72)
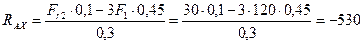 Н.
Н.
Из уравнения (4.70)
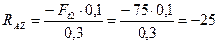 Н.
Н.
Из уравнения (4.68)
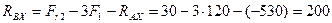 Н.
Н.
Из уравнения (4.69)
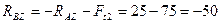 Н.
Н.
Следует отметить, что уравнение 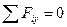 даст тождество 0 = 0.
даст тождество 0 = 0.
Полная реакция опоры А
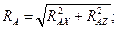
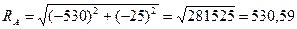 Н.
Н.
Полная реакция опоры В
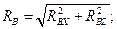
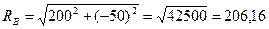 Н.
Н.
Ответ: 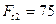 Н;
Н; 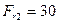 Н;
Н; 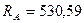 Н;
Н; 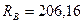 Н.
Н.
Пример 116. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 4.25, a. Определить силы 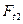 и
и 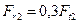 , а также реакции опор А и В, если F 1 = 100 H.
, а также реакции опор А и В, если F 1 = 100 H.
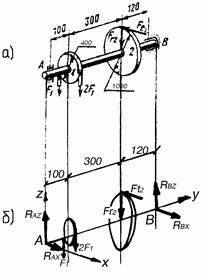
Рис. 4.25. К примеру 116
Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие 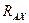 ,
, 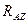 , и
, и 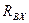 ,
, 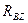 (рис. 4.25, б).
(рис. 4.25, б).
Составляем уравнения равновесия сил, произвольно расположенных в пространстве:
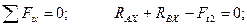 (4.73)
(4.73)
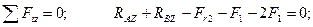 (4.74)
(4.74)
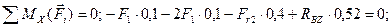 (4.75)
(4.75)
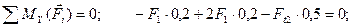 (4.76)
(4.76)
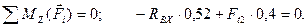 (4.77)
(4.77)
Из уравнения (4.76)
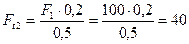 Н.
Н.
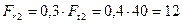 Н.
Н.
Из уравнения (4.77)
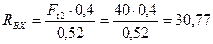 Н.
Н.
Из уравнения (4.75)
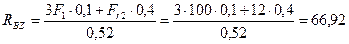 Н.
Н.
Из уравнения (4.74)
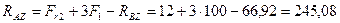 Н.
Н.
Из уравнения (4.73)
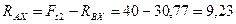 Н.
Н.
Следует отметить, что уравнение 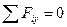 даст тождество 0 = 0.
даст тождество 0 = 0.
Полная реакция опоры А
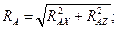
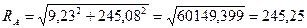 Н.
Н.
Полная реакция опоры В
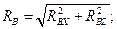
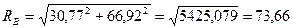 Н.
Н.
Ответ: 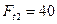 Н;
Н; 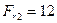 Н;
Н; 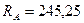 Н;
Н; 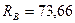 Н.
Н.
Пример 117. На вал жестко насажены шкив 1 и колесо 2, нагруженные, как показано на рис. 4.26, a. Определить силу 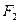 , а также реакции опор А и В, если F 1 = 220 H.
, а также реакции опор А и В, если F 1 = 220 H.
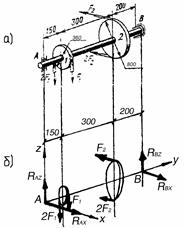
Рис. 4.26. К примеру 117
Решение. Отбрасывая связи вала (подшипники), прикладываем к валу их реакции, разложенные на составляющие 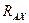 ,
, 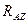 и
и 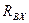 ,
, 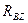 (рис. 4.26, б).
(рис. 4.26, б).
Составляем уравнения равновесия сил, произвольно расположенных в пространстве:
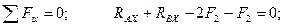 (4.78)
(4.78)
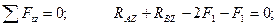 (4.79)
(4.79)
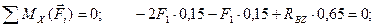 (4.80)
(4.80)
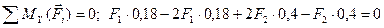 ; (4.81)
; (4.81)
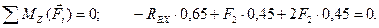 (4.82)
(4.82)
Из уравнения (4.81)
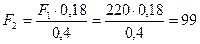 Н.
Н.
Из уравнения (4.82)
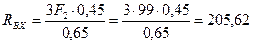 Н.
Н.
Из уравнения (4.80)
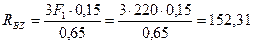 Н.
Н.
Из уравнения (4.78)
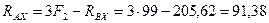 Н.
Н.
Из уравнения (4.79)
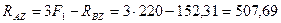 Н.
Н.
Следует отметить, что уравнение 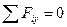 даст тождество 0 = 0.
даст тождество 0 = 0.
Полная реакция опоры А
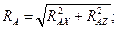
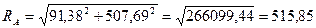 Н.
Н.
Полная реакция опоры В
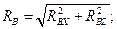
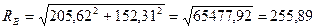 Н.
Н.
Ответ: 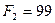 Н;
Н; 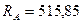 Н;
Н; 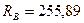 Н.
Н.
Пример 118. Горизонтальный провод АЕ, натяжение которого равно 400 Н, подвешен к вертикальному столбу АВ, укреплённому оттяжками АС и АD, расположенными симметрично относительно плоскости ВАЕ. Известно: АВ = 5 м, ВС = BD = 4 м, Ð СВD = 150°. Определить натяжение оттяжек и усилие в столбе (рис. 4.27, а).
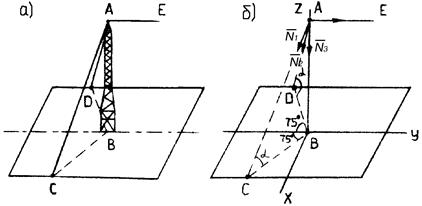 |
Рис. 4.27. К примеру 118
Решение. Рассмотрим равновесие сходящихся сил, приложенных к узлу А. Задаваемая сила N – реакция провода АЕ, реакция 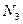 столба АВ и реакции N 1 и N 2 оттяжек АС и AD не лежат в одной плоскости. Три неизвестные силы
столба АВ и реакции N 1 и N 2 оттяжек АС и AD не лежат в одной плоскости. Три неизвестные силы 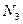 , N 1 и N 2 определим из трёх уравнений равновесия сходящихся сил в пространстве:
, N 1 и N 2 определим из трёх уравнений равновесия сходящихся сил в пространстве:
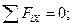
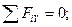
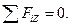
Для этого проведём оси координат из точки В, направив ось Z вдоль ВА, ось Y – параллельно АЕ и ось Х - перпендикулярно осям Y и Z (рис. 4.27, б). Приложим к узлу А все действующие на него силы, направив их от узла, т. е. предположив, что все элементы растянуты. При проецировании сил N 1 и N 2 на оси Х и Y применим двойное проецирование, так как углы, составленные этими силами с осями Х и Y, не даны. Спроецируем сначала каждую из этих сил на плоскость XBY и полученную проекцию спроектируем на соответствующую ось.
Вычислим предварительно
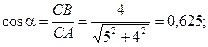
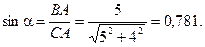
Составим уравнения равновесия сил:
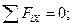
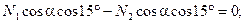 (4.83)
(4.83)
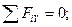
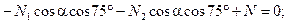 (4.84)
(4.84)
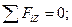
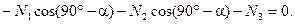 (4.85)
(4.85)
Из уравнения (4.83) получаем
N 1 = N 2.
Из уравнения (4.84) найдём эти силы:
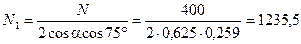 Н.
Н.
N 1 = N 2 = 1235,5 Н (натяжения симметричных оттяжек одинаковы).
Из уравнения (4.85) определим 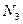 :
:
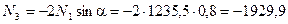 Н.
Н.
Вертикальный столб АВ сжат.
Ответ: 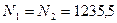 Н;
Н; 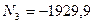 Н.
Н.
Пример 119. Определить усилия в стержне пространственной фермы, изображённой на рис. 4.28, а также реакции опор фермы K, L, M, N, если на узел А фермы действуют вертикальная сила 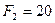 кН и горизонтальная сила
кН и горизонтальная сила 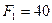 кН, направленная вдоль стержня AF,
кН, направленная вдоль стержня AF, 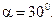
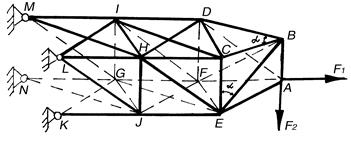
Рис. 4.28. К примеру 119
Решение. Для определения усилий в стержнях 1-39 фермы воспользуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются, то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил, действующих на каждый узел.
Узлы фермы вырезаем в такой последовательности, при которой число неизвестных сил в рассматриваемом узле не превышает трех. Так же, как и при определении усилий в стержнях плоских ферм, все стержни фермы условимся считать растянутыми; знак «минус» у вычисленной реакции стержня покажет, что стержень сжат.
Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы А, В, С, D, E, F, H, I, J, K, L (см. рис. 4.28).
Для определения усилий в стержнях пространственной фермы воспользуемся способом вырезания узлов (рис. 4.29).
Узел А:
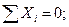
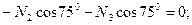
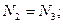
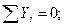
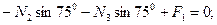
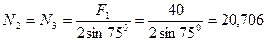 кН.
кН.
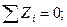
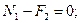
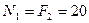 кН.
кН.
Узел В:
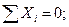
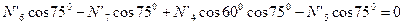 ;
;
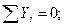
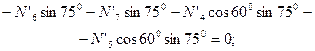
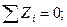
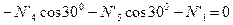 .
.
В силу симметрии
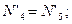
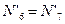 ;
; 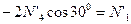 ;
;
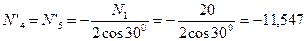 кН;
кН;
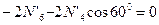 ;
; 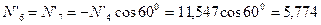 кН.
кН.
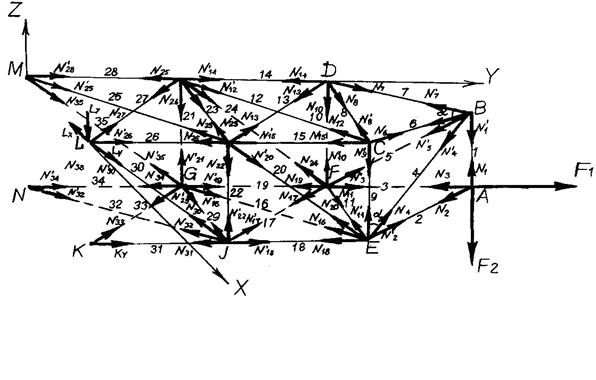
 Рис. 4.29. К примеру 119
Рис. 4.29. К примеру 119
Рассматривая узлы C и D, получим:
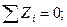
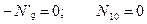 - усилия в стержнях 9 и 10 равны нулю.
- усилия в стержнях 9 и 10 равны нулю.
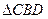 :
: 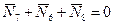 ,
,
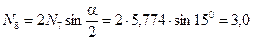 кН.
кН.
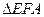 :
: 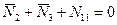 ,
,
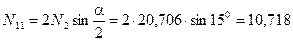 кН.
кН.
Узел D:
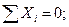
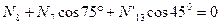 (IHCD – квадрат);
(IHCD – квадрат);
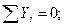
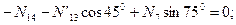
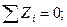
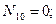
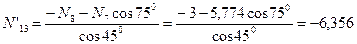 кН.
кН.
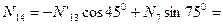
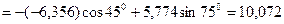 кН.
кН.
В силу симметрии для узла С
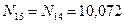 кН;
кН; 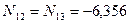 кН.
кН.
Узел E:
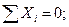
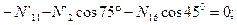
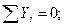
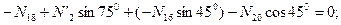
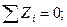
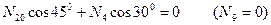 ;
;
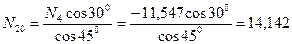 кН.
кН.
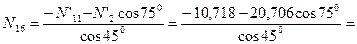
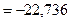 кН;
кН;
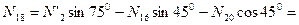
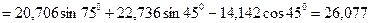 кН.
кН.
В силу симметрии для узла F
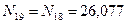 кН;
кН; 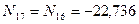 кН;
кН; 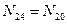 .
.
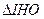 :
: 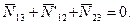
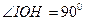 ,
, 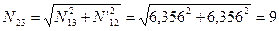 кН.
кН.
Узел H:
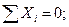
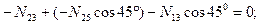
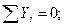
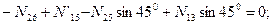
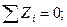
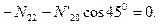
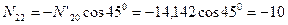 кН;
кН;
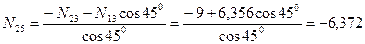 кН;
кН;
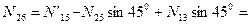
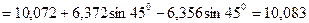 кН.
кН.
Для узла I в силу симметрии
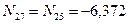 кН;
кН; 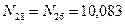 кН;
кН;
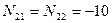 кН.
кН.
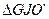 :
: 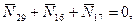
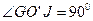 ,
, 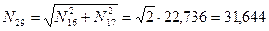 кН.
кН.
Узел J:
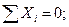
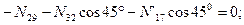
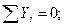

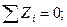
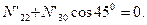
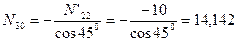 кН;
кН;

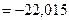 кН;
кН;
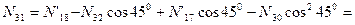
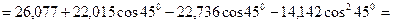
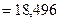 кН.
кН.
Для узла G в силу симметрии
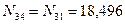 кН;
кН; 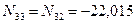 кН;
кН;
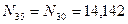 кН.
кН.
Основываясь на результатах расчета, можно установить следующее:
1. Если в незагруженном узле фермы сходятся три стержня, не лежащие в одной плоскости, то усилия в каждом из этих стержней равны нулю.
2. Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю.
Эти соображения, дающие возможность без вычислений определить стержни с нулевыми усилиями, значительно упрощают определение усилий в стержнях пространственных ферм.
Определив усилия в стержнях фермы способом вырезания узлов, можно определить реакции опор, представляющих собой шаровые шарниры. Реакцию каждой опоры неизвестного направления разложим на три составляющие, направленные вдоль осей координат. Эти составляющие определим из уравнений равновесия сил, приложенных к опорным узлам.
Узел K:
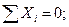
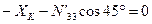 ;
;
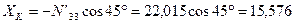 кН;
кН;
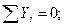
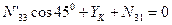 ;
; 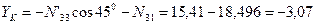 кН.
кН.
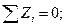
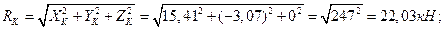
Узел L:
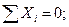
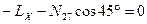 ;
;
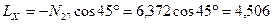 кН;
кН;
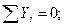
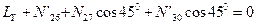 .
.
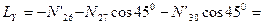
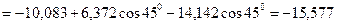 кН.
кН.
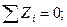
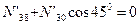 ;
;
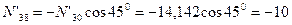 кН;
кН;
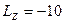 кН;
кН;
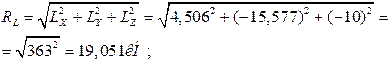
Для узла М в силу симметрии
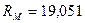 кН;
кН;
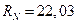 кН.
кН.
Результаты расчётов сводим в табл. 4.2.
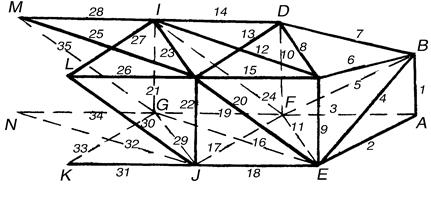
Рис. 4.30. К примеру 119
Таблица 4.2
Результаты расчётов
| Стержни | |||||||
| Усилие N, кH | 20,706 | 20,706 | -11,547 | -11,547 | 5,774 | 5,774 |
| Стержни | |||||||
| Усилие N, кH | 3,0 | 10,718 | -6,356 | -6,356 | 10,072 |
| Стержни | |||||||
| Усилие N, кH | 10,072 | -22,736 | -22,736 | 26,076 | 26,077 | 14,142 | -10 |
| Стержни | |||||||
| Усилие N, кH | -10 | 14,142 | -6,372 | 10,083 | -6,372 | 10,083 |
| Стержни | |||||||
| Усилие N, кH | 31,644 | 14,142 | 18,496 | -22,015 | -22,015 | 18,496 | 14,142 |
Реакции шарниров:
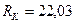 кН;
кН; 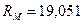 кН;
кН;
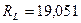 кН;
кН; 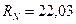 кН.
кН.
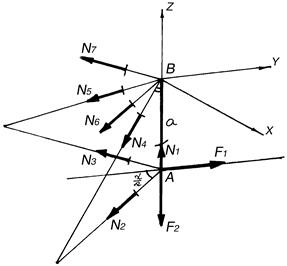 |
Рис. 4.31. К примеру 119
В – точка Риттера.
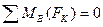 ;
; 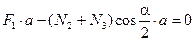 ;
;
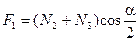 .
.
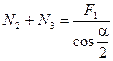 .
.
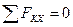 ;
; 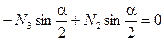 .
.
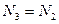 ;
; 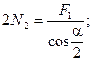
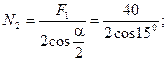
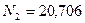 кН;
кН; 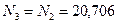 кН.
кН.
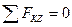 ;
; 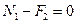 ;
; 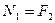 ,
, 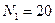 кН.
кН.
Дата добавления: 2015-08-02; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение | | | Задачи к заданиям |