Решение. 1. Пренебрегая размерами блока, считаем, что заданные силы и искомые реакции стержней

1. Пренебрегая размерами блока, считаем, что заданные силы и искомые реакции стержней приложены к точке D - вершине трехгранной пирамиды, образуемой треногой. На точку D действуют вертикально вниз и горизонтально влево силы натяжения ветвей троса, равные силе тяжести груза F, а также три реакции R_A, R_B и R_C стержней треноги.

2. Систему пяти сил, действующих на точку D, в выбранных осях координат изобразим на рис. 4.13, б; реакции R_A, R_B и R_C стержней направлены вдоль стержней от точки D (из предположения, что все стержни растянуты).

3. Прежде чем приступить к составлению уравнений равновесия, следует заметить, что силы, лежащие в плоскости, перпендикулярной какой-либо оси, проецируются на эту ось в виде точки (т.е. проекции равны нулю). Например, обе силы F (вертикальная и горизонтальная) и сила R_C лежат в плоскости, перпендикулярной оси Х. Поэтому на ось Х проецируются лишь силы R_A и R_B. Рассуждая аналогично, видим, что на ось Y проецируются все силы, кроме вертикальной силы F, и на ось Z - также все силы, за исключением горизонтальной силы F.

Составим уравнения равновесия:

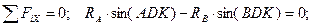(4.24)

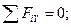
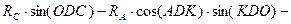
(4.25)

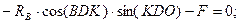
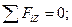
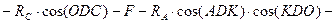(4.26)

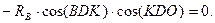
Так как Ð ADK = Ð BDK = Ð KDO = 30° и Ð ODC = 45°, из уравнения (4.24) находим, что R_A = R_B.

Уравнения (4.25) и (4.26) запишем теперь в виде

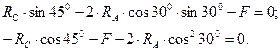
Складывая эти уравнения и учитывая, что sin30° = 0,5 и 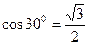, получаем

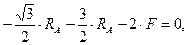
откуда

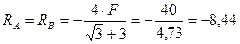кН.

Стержни AD и BD треноги сжаты силой 8,44 кН.

Теперь, зная R_A, найдем

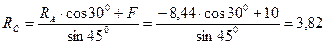кН.

Стержень CD растянут силой 3,82 кН.

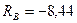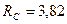Ответ: кН; кН; кН.

Пример 106. Определить усилия в стержнях пространственной фермы, изобра­женной на рис. 4.14, а также реакции опор фермы Е, F, К и L, если на узел В фермы действует вертикальная сила F ₁ = 50 кН, на узел С - горизонтальная сила F ₂ = 25 кН, направленная вдоль стержня CD. Размеры указаны на рисунке.

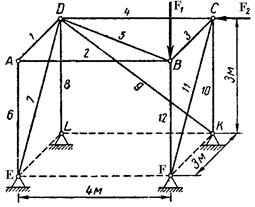
Рис. 4.14. К примеру 106

Решение. Для определения усилий в стержнях 1-12 фермы воспользуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются, то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил, действующих на каждый узел.

Узлы фермы вырезаем в такой последовательности, при которой число неиз­вестных сил в рассматриваемом узле не превышает трех. Так же, как и при определении усилий в стержнях плоских ферм, все стержни фермы условимся считать растянутыми; знак «минус» у вычисленной реакции стержня покажет, что стержень сжат.

Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы А, В, С и D (рис. 4.15).

Узел А:

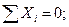
(4.27)

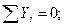
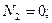(4.28)

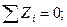
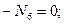
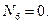(4.29)

Так как узел А не загружен внешней силой, а сходящиеся силы N ₁, N ₂ и N ₆, не лежащие в одной плоскости, не могут уравновешиваться, то они равны нулю.

Рис. 4.15. К примеру 106

Узел В:

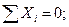
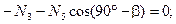(4.30)

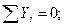
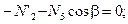(4.31)

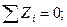
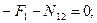
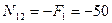кН. (4.32)

Из уравнения (4.31)

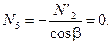
Из уравнения (4.30)

.

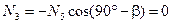Узел С:

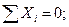
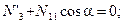(4.33)

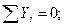
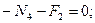
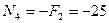кН; (4.34)

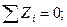
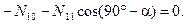(4.35)

Из уравнения (4.33)

Из уравнения (4.35)

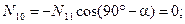
Узел D:

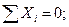
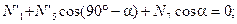(4.36)

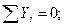
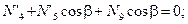(4.37)

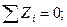
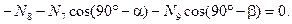(4.38)

Найдем синусы и косинусы углов a и b.

Так как

AD = DL, тo a = 45°;

cosa = sina =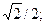

cosb = АВ / DB = 4 / 5 = 0,8;

sinb = AD / DB = 3 / 5 = 0,6.

Из уравнения (4.36)

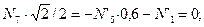
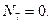
Из уравнения (4.37)

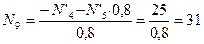кН.

Из уравнения (4.38)

кН.

Таблица 4.1

Результаты расчётов

Стержни
Усилие N, кH				-25				-19				-50

Основываясь на результатах расчета, можно установить следующее:

1. Если в незагруженном узле фермы сходятся три стержня, не лежащие в одной плоскости, то усилия в каждом из этих стерж­ней равны нулю (узел А, стержни 1, 2 и 6).

2. Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю (узел С, стержень 11 при ).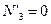

Эти соображения, дающие возможность без вычислений опре­делить стержни с нулевыми усилиями, значительно упрощают опре­деление усилий в стержнях пространственных ферм.

Определив усилия в стержнях фермы способом вырезания узлов, можно определить реакции опор, представляющих собой шаровые шарниры. Реакцию каждой опоры неизвестного направления раз­ложим на три составляющие, направленные вдоль осей координат. Эти составляющие определим из уравнений равновесия сил, при­ложенных к опорным узлам.

Узел Е:

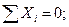
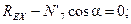(4.39)

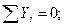
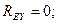(4.40)

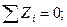
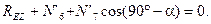(4.41)

Из уравнения (4.39)

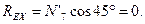
Из уравнения (4.41)

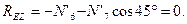
Так как

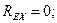
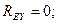
то R_E = 0, т. е. опора Е не нагружена.

Узел F:

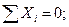
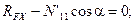(4.42)

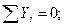
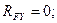(4.43)

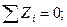
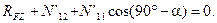(4.44)

Из уравнения (4.42)

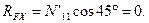
Из уравнения (4.44)

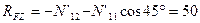кН.

Знак «плюс» в ответе указывает на то, что истинное направление составляю­щей R_FZ совпадает с направлением, указанным на схеме.

Так как R_FХ = 0 и R_FY = 0, то реакция опоры направлена вертикально вверх и имеет модуль R_F = | R_FZ | = 50 кН.

Узел К:

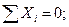
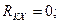(4.45)

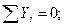
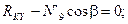(4.46)

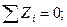
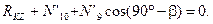(4.47)

Из уравнения (4.46)

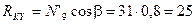кН.

Из уравнения (4.47)

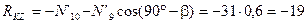кН.

Знаки ответов показывают, что принятое направление силы R_KY совпадает с действительным, а силы R_KZ - противоположно действительному (см. рис. 4.15).

Определим модуль и направление реакции R_K:

кН;

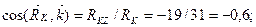
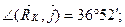
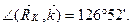
Узел L:

Так как в узле L не известна лишь реакция R_L, то составляем только одно уравнение:

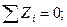
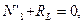
откуда

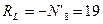кН.

Знак «плюс» в ответе указывает на то, что реакция R_L направлена вертикально вверх.

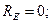
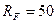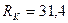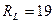Ответ: кН; кН; кН.

Пример 107. Жестко заделанная балка длиной l = 1,4 м и квадратным поперечным сечением со стороной a = 0,2 м (рис. 4.16, а) нагружена горизонтальной силой F = 2 кH и вертикальной равномерно распределенной нагрузкой интенсивностью q = 1 кН/м. Определить реакции заделки.

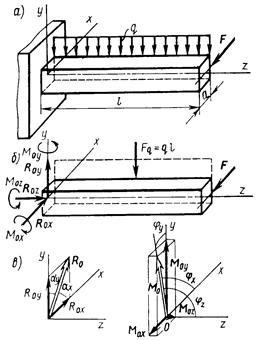
Рис. 4.16. К примеру 107

Дата добавления: 2015-08-02