Читайте также:
|
Всякую силу F, приложенную к твёрдому телу в точке А, можно переносить параллельно линии её действия в любую точку О, присоединив пару сил, момент которой равен моменту данной силы относительно новой точки её приложения.
Докажем эту теорему. Пусть в точке А твёрдого тела приложена сила F (рис. 4.2, а). Выберем произвольную точку О (точку приведения), не лежащую на линии действия силы F. Приложим в точке О параллельно данной силе F две равные по модулю, но противоположные по направлению силы F ¢ и F ¢¢ (рис. 4.2, б). Полученная система сил (F, F ¢, F ¢¢) эквивалентна одной силе F.
Силы F и F ¢ образуют пару (F, F ¢). Следовательно, система сил (F, F ¢, F ¢¢) эквивалентна силе F ¢¢, приложенной в точке О и равной по модулю силе F, и паре сил (F, F ¢) с моментом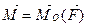 
(рис. 4.2, в).
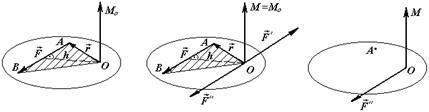
а) б) в)
Рис. 4.2. Приведение силы к центру
Дата добавления: 2015-08-02; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Момент силы относительно оси | | | Равновесие твёрдых тел под действием пространственной системы сил |