Решение. Составная балка АВС находится в равновесии, следовательно, балки АВ и ВС также находятся в равновесии.

Рассмотрим условия равновесия каждой балки в системе координат Аху (рис. 3.60, б). На балку ВС действуют активная сила F и реакции связей R_C, R_BX, R_BY. Реакция R_C подвижной опоры балки ВС направлена по нормали к поверхности опоры. Ни модуль, ни направление реакции R_B в шарнире В не известны. Поэтому она представлена в виде двух составляющих: R_BX, R_BY.

На балку АВ действуют равномерно распределённая нагрузка q, равнодействующая которой Q = ql приложена в середине балки АВ и направлена перпендикулярно к её оси, реакции связе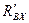й и , которые, согласно закону действия и противодействия, имеют одинаковые модули и противоположные силам и направления (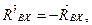 ), реакции и пара сил с моментом М_А. Итак, балка АВ находится в равновесии при действии сил и реактивной пары сил с моментом М_{А .}

Составим уравнения равновесия балки ВС:

;

;

.

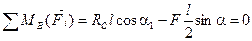Уравнения равновесия балки АВ:

;

;

.

Решив эти системы уравнений при найдём:

кН;

кН;

кН;

кН;

кН;

кН×м.

Так как реакции в шарнире В, действующие на балки АВ и ВС, направлены в противоположные стороны, получаем кН, кН.

Полная реакция опоры :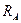

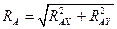; кН.

Ответ: кН; кН×м; кН.

Пример 95. На губки схвата манипулятора при удержании детали действует сила F = 6 кH (рис. 3.61, а). Найти реакции в шарнирах А, В, С и силу привода F_П, если h ₁ = 180 мм, h ₂ = 120 мм, а углы g₁ = 7°, g₂ = 9°. Силами трения и силами тяжести звеньев пренебречь.

Решение. Сначала рассмотрим равновесие звена 2 (рис. 3.61, б).

На него действует сила F, реакция F ₂₁ звена 1, направленная вдоль его оси, и реакция шарнира А, представленная её составляющими R_AX, R_AY.

Составим уравнения равновесия звена 2:

;

;

,

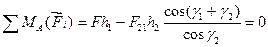откуда:

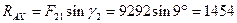Н;

Н;

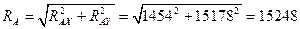Н;

Н.

Рис.3.61. К примеру 95

Сила, действующая на звено 1 и направленная вдоль его оси, F ₁₂ = F ₂₁ = 9292 H.

Рассматривая равновесие шарнира С (рис. 3.61, в), определим силу привода:

Н.

Найденные величины используются для расчёта на прочность деталей схвата.

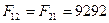Ответ: Н; Н; Н.

Пример 96. Определить усилия в стержнях 8, 9 и 10 фермы, изображённой на рис. 3.62, а, если F ₁ = 50 кH, F ₂ = 70 кH, F ₃ = 15 кH, F ₄ = 35 кH, F ₅ = 15 кH, AB = 4 a, KD = 2 a.

а)

б) в)

Рис. 3.62. К примеру 96

Решение. Прежде всего определим реакции опор фермы R_AX, R_AY, R_B (рис. 3.62, б). Для этого составим три уравнения равновесия сил, действующих на ферму:

; ;

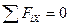кН;

; ;

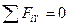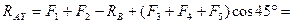
кН;

; ;

кН.

Для определения усилий в стержнях 8, 9 и 10 проведём сечение I-I. Отбросим левую часть фермы, заменив её действие на оставшуюся часть реакциями разрезанных стержней N ₈, N ₉ и N ₁₀, направив эти силы в сторону отброшенной части (рис. 3.62, в). Чтобы определить каждое усилие независимо от двух других, применим систему уравнений равновесия.

Составим уравнения моментов сил, действующих на правую часть фермы, относительно точек Риттера К, В и L, в которых пересекаются по две линии действия усилий:

; ;

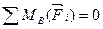кН;

; ;

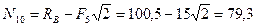кН;

; ;

кН.

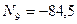Ответ: кН; кН; кН.

Дата добавления: 2015-08-02