Общий случай нагружения тонкостенного стержня. Бимомент

В общем случае нагружения осевые перемещения сечения тон­костенного бруса можно представить в виде следующего выраже­ния:

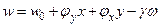, (19.8)

где , и характеризуют: смещение по продольной оси z; поворот сечения как жесткого целого относительно координатных осей x и y; - удельный угол закручивания относительно продоль­ной оси z, 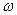- эпюра главной секториальной площади.

Нормальные напряжения в сечении, согласно закону Гука, в данном случае определяются согласно выражения:

. (19.9)

С учетом последнего выражения, формулы по определению внутренних силовых факторов от нормальных напряжений , при­мут вид:

(19.10)

Здесь через обозначена новая силовая характеристика, назы­ваемая бимоментом, размерность которой будет кНм².

В результате совместного рассмотрения (19.9) и (19.10) выражение нормальных напряжений можно представить в следующем виде:

. (19.11)

Первые три слагаемых уже известные нам величины нормаль­ных напряжений из курса «Сопротивления материалов», являются результатом действия продольной силы и изгибающих моментов. Что же касается четвертого слагаемого, то оно характеризует изме­нения, вносимые в линейные законы распределения напряжений, депланацией сечения, силовой мерой которой является бимомент.

Заметим, что бимомент является самоуравновешенным фак­тором и по методу сечений не может быть определен. Следова­тельно, задача в общем случае нагружения тонкостенного стержня является статически неопре­делимой. Например, если на­грузить стержень двутаврово­го сечения четырьмя равны­ми силами Р (рис.19.5), бимо­мент в торцевом сечении бу­дет равен:

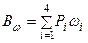, (19.12)

где - значение секториаль­ной площади для точки при­ложения силы P_i, т.е.:

.

Рис. 19.5

В этом случае, очевидно, что и продольная сила N, и изгиба­ющие моменты M_x , M_y равны нулю.

Касательные напряжения в поперечном сечении стержня в общем случае нагружения слагаются из касательных напряжений поперечного изгиба, простого (свободного) кручения, и наконец, из вторичных касательных напряжений, возникающих за счет стесненного кручения:

. (19.13)

Следовательно, в общем случае нагружения в поперечных сечениях тонкостенного стержня возникают следующие внутренние усилия: Q_x, Q_y - поперечные силы, от касательных напряжений 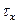, ; M_x, M_y -изгибающие моменты, от нормальных напряжений ; M_z - кру­тящий момент свободного кручения от касательных напряжений ; - бимомент от действующих нормальных напряжений , вследствии изгиба элементов тонкостенного стержня; - изгиб­но- крутящий момент от дополнительных касательных напря­жений .

Формулы для вычисления перечисленных факторов даны в таблице 19.6, где приняты следующие обозначения: u, v - перемещения линий центров изгиба сечений в направлении координатных осей x и y; - соответственно, статические моменты относитель­но координатных осей и секториально статический момент отсе­ченной части сечения, расположенной по одну сторону от расчет­ной точки.

Все эти величины легко определяются, если известна функция . Последняя может быть найдена из условия равенства суммы крутящих моментов стесненного и свободного кручения полному крутящему моменту:

. (19.14)

Подставляя в (19.14) значения и из табл. 19.1, получим:

. (19.15)

Дифференцируя (15.15) по z, имеем:

, (19.16)

или

, (19.17)

где - изгибно-крутиль­ная характеристика поперечного сечения стержня; 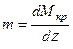-распре­деленный крутящий момент.

Таблица 19.6

Силовой фактор	Усилие	Напряжение
Поперечная сила Qx, Qy	,	,
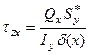Изгибающий момент Mx, My	,	,
Крутящий момент при свободном кручении тонкостенного стержня постоянной толщины стенки , Mz
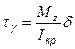
Крутящий момент при стеснен­ном кручении тонкостенного стер­жня постоянной толщины стенки ,
Бимомент

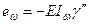
Рис. 19.6

Рассмотрим случай кручения, когда на свободном конце тон­костенного стержня, защемленного с другим концом, действует крутящий момент (рис.19.6). В этом случае имеем:

, (19.18)

интеграл которого записывается:

. (19.19)

Откуда имеем:

(19.20)

Для определения C ₁, C ₂, C ₃ и C ₄ с учетом граничных условий:

при z = 0, и ;

при z = l, и , (19.21)

получим:

(19.22)

Учитывая выражения произвольных постоянных (19.22) из (19.19) и (19.20), будем иметь:

(19.23)

Здесь sh x и ch x - гиперболический синус и гиперболический косинус, соответственно, аргумента x:

. (19.24)

В заключении, учитывая (19.23) и выражения усилий из таблицы 19.1, окончательно получим:

(19.25)

Заметим, что существует полная аналогия в основных зависи­мостях теории стесненного кручения стержней открытого и замк­нутого профилей. Основные расчетные зависимости теории расчета стержней замкнутого профиля можно получить, путем замены в приведенных выше зависимостях для расчета стержней открытого профиля, уже известных нам секториальных координат и сектори­альных геометрических характеристик сечений 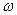, и т.д., на обобщенные величины , и т.д., для замкнутого профиля.

При этом, главная обобщенная секториальная координата , для замкнутого профиля (рис.19.7), определяется:

где - сектори­альная координата, вычисляемая по аналогии теории стержня от­крытого профиля; r - длина пер­пендикуляра, опущенного из по­люса А, взятого внутри контура, на касательную к контуру; - параметр, условно на­зываемый «средним радиусом» замкнутого контура; 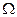- удвоенная площадь, охваченная срединной линией контура s; 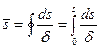-приведенная длина дуги данной точки контура.

Рис. 19.7

Главный обобщенный секториальный момент сечения и секториальный статический момент 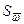для замкнутого контура определяются по формулам:

,

где .

Дата добавления: 2015-08-10