
|
Читайте также: |
Наряду с общепринятыми, для тонкостенных стержней вводятся дополнительные характеристики поперечных сечений.
Секториально статический момент поперечного сечения:
 , см4 .
, см4 .
Секториально линейные моменты площади поперечного сечения:
 и
и  , см5 .
, см5 .
Секториальный момент инерции поперечного сечения:
 , см6 .
, см6 .
Окончательные выражения секториальных характеристик, исходя из предположения, что толщина тонкостенного сечения по всему контуру постоянна и равна d.
При поперечном изгибе или кручении всегда существует такая точка, относительно которой момент от касательных сил, возникающих в поперечном сечении, равен нулю. Эта точка называется центром изгиба или кручения. Для сечений, имеющих две оси симметрии, центр изгиба или центр кручения совпадают с центром тяжести.
Положение центра изгиба (или кручения) не зависит от действующих на стержень сил, а зависит только от формы и размеров поперечного сечения тонкостенного стержня.
При стесненном кручении центр кручения, а также начало отсчета секториальной площади не могут быть выбраны произвольно. Эти точки должны быть выбраны так, чтобы секториально линейные моменты, а также секториально статический момент были равны нулю, т.е.:
 (19.4)
(19.4)
Выполнение условий первых двух условий из (19.4) зависит только от выбора координат полюса. Выполнение же третьего из условий (19.4) зависит от выбора начала отсчета 0.
Эпюра 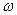 , построенная при полюсе, в качестве которого взят центр изгиба, и удовлетворяющая третьему уравнению (15.4), носит название эпюры главной секториальной площади.
, построенная при полюсе, в качестве которого взят центр изгиба, и удовлетворяющая третьему уравнению (15.4), носит название эпюры главной секториальной площади.
Положение центра изгиба и секториальные характеристики сечения на практике определяются в следующей последовательности.
Сначала выбирается положение полюса Р и строится эпюра секториальной площади 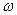 ¢ относительно полюса.
¢ относительно полюса.
Далее определяются величины  и
и  относительно полюса P и вычисляются координаты центра изгиба по формулам:
относительно полюса P и вычисляются координаты центра изгиба по формулам:
 и
и  . (19.5)
. (19.5)
Определяется секториальная площадь относительно центра изгиба по формуле (19.3) и вычисляется секториaльно стaтический момент поперечного сечения по формуле:
 ,
,
как площадь эпюры  , умноженную на
, умноженную на  .
.
Далее определяется постоянная D из третьего условия (19.4) по формуле:
 (19.6)
(19.6)
и строится эпюра главной секториальной площади:
 . (19.7)
. (19.7)
Секториальные геометрические характеристики прокатных двутавров и швеллеров приведены в табл.19.1 и 19.2, значения моментов инерции при чистом кручении прокатных уголков приведены в табл.19.3 и 19.4., а формулы координат центра изгиба и секториальных моментов инерции некоторых металлических профилей – в табл.19.5.
Таблица 19.1

| Секториальные геометрические характеристики прокатных двутавров (ОСТ 10016-39) | ||||
| Номер профиля | Секториальный
момент
инерции
 , см6 , см6
| Секториальная
площадь для
крайней точки
профиля
 , см2 , см2
| Секториальный
момент
сопротивления
 , см4 , см4
| Момент
инерции
при
чистом
кручении
 , см4 , см4
| Изгибно-крутильная
характеристика
 , см-1 , см-1
|
| 644,3 | 15,25 | 42,26 | 2,873 | 0,04122 | |
| 20,10 | 67,33 | 4,243 | 0,03457 | ||
| 25,54 | 100,23 | 5,911 | 0,02966 | ||
| 32,25 | 151,30 | 8,406 | 0,02562 | ||
| 38,90 | 211,28 | 11,37 | 0,02295 | ||
| 20а | 46,15 | 284,31 | 14,81 | 0,02074 | |
| 20б | 47,05 | 284,50 | 17,85 | 0,02215 | |
| 22а | 55,91 | 407,33 | 20,32 | 0,01844 | |
| 22б | 56,90 | 420,55 | 24,08 | 0,01958 | |
| 24а | 64,48 | 524,15 | 25,57 | 0,01698 | |
| 24б | 65,57 | 540,25 | 30,12 | 0,01800 | |
| 27а | 76,68 | 690,99 | 31,93 | 0,01515 | |
| 27б | 77,92 | 711,21 | 37,60 | 0,01608 | |
| 30а | 88,38 | 867,93 | 38,83 | 0,01389 | |
| 30б | 89,75 | 892,60 | 45,78 | 0,01475 | |
| 30с | 91,13 | 917,50 | 55,23 | 0,01587 | |
| 33а | 100,69 | 1064,3 | 46,19 | 0,01281 | |
| 33б | 102,21 | 1093,6 | 54,49 | 0,01363 | |
| 33с | 103,73 | 1123,3 | 65,74 | 0,01466 | |
| 36а | 115,19 | 1344,0 | 56,85 | 0,01183 | |
| 36б | 116,85 | 1379,6 | 66,72 | 0,01256 | |
| 36с | 118,51 | 1415,6 | 79,99 | 0,01348 | |
| 40а | 134,13 | 1706,6 | 68,75 | 0,01070 | |
| 40б | 136,00 | 1749,6 | 80,68 | 0,01137 | |
| 40с | 137,85 | 1793,3 | 96,55 | 0,01220 | |
| 45а | 159,75 | 2357,6 | 95,31 | 0,009819 | |
| 45б | 161,96 | 2414,4 | 111,3 | 0,01041 | |
| 45с | 163,96 | 2471,5 | 131,8 | 0,01113 | |
| 50а | 187,10 | 3270,9 | 131,2 | 0,009038 | |
| 50б | 189,44 | 3346,2 | 150,3 | 0,009504 | |
| 50с | 191,79 | 3421,8 | 174,9 | 0,01007 | |
| 55а | 216,79 | 4180,8 | 159,9 | 0,008198 | |
| 55б | 219,36 | 4272,5 | 182,7 | 0,008617 | |
| 55с | 221,94 | 4364,8 | 211,5 | 0,009119 | |
| 60а | 251,22 | 5373,4 | 195,5 | 0,007427 | |
| 60б | 254,04 | 5484,2 | 221,9 | 0,007790 | |
| 60с | 256,86 | 5595,7 | 255,3 | 0,008226 |
Примечание: При вычислении  приняты
приняты 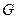 =8∙104 МПа,
=8∙104 МПа,  =2,1∙105 МПа
=2,1∙105 МПа
Таблица 19.2
| Секториальные геометрические характеристики прокатных швеллеров (ОСТ 10016-39) | |||||||
| Номер профиля | Координаты
центра
изгиба
 , см , см
| Секториальный
момент
инерции
 , см6 , см6
| Секториальные площади | Секториальные моменты сопротивления | Момент
инерции
при
чистом
кручении
 , см4 , см4
| Изгибно-крутильная
характеристика
 , см-1 , см-1
| ||
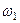 ,
см2 ,
см2
|  ,
см2 ,
см2
|  ,
см4 ,
см4
|  ,
см4 ,
см4
| |||||
| 1,08 | 24,91 | 2,70 | 4,26 | 9,22 | 5,85 | 1,350 | 0,14370 | |
| 6,5 | 1,15 | 64,88 | 3,86 | 6,36 | 16,80 | 10,21 | 1,497 | 0,09375 |
| 1,22 | 141,8 | 5,15 | 8,75 | 27,57 | 16,20 | 1,940 | 0,07219 | |
| 1,34 | 254,8 | 7,19 | 12,71 | 49,35 | 27,92 | 2,727 | 0,05411 | |
| 1,48 | 768,3 | 9,54 | 17,31 | 80,51 | 44,39 | 3,634 | 0,04245 | |
| 14а | 1,58 | 12,03 | 22,63 | 125,74 | 66,85 | 4,815 | 0,03483 | |
| 14б | 1,39 | 11,46 | 23,85 | 149,32 | 71,75 | 6,248 | 0,03730 | |
| 16а | 1,68 | 14,74 | 28,63 | 187,23 | 96,40 | 6,306 | 0,02950 | |
| 16б | 1,48 | 14,03 | 30,09 | 220,87 | 103,00 | 8,227 | 0,03180 | |
| 18а | 1,83 | 17,68 | 35,32 | 268,41 | 134,34 | 8,128 | 0,02555 | |
| 18б | 1,57 | 16,83 | 37.02 | 314,50 | 142,95 | 10,50 | 0,02749 | |
| 20а | 1,94 | 21,27 | 42,46 | 361,95 | 181,28 | 9,84 | 0,02207 | |
| 20б | 1,73 | 20,24 | 44,45 | 422,87 | 192,57 | 12,50 | 0,02359 | |
| 22а | 2,07 | 24,84 | 49,60 | 466,69 | 233,73 | 11,66 | 0,01958 | |
| 22б | 1,86 | 23,63 | 51,88 | 544,42 | 247,95 | 14,60 | 0,02079 | |
| 24а | 2,10 | 27,48 | 55,21 | 557,74 | 277,59 | 13,21 | 0,01812 | |
| 24б | 1,88 | 26,10 | 57,75 | 651,56 | 394,50 | 16,47 | 0,01921 | |
| 24с | 1,67 | 24,91 | 60,09 | 748,35 | 310,21 | 21,31 | 0,02087 | |
| 27а | 2,14 | 31,85 | 66,46 | 764,11 | 366,19 | 16,25 | 0,01505 | |
| 27б | 1,91 | 30,23 | 69,39 | 889,34 | 387,42 | 20,34 | 0,01698 | |
| 27с | 1,70 | 28,82 | 72,10 | 1018,6 | 407,14 | 26,34 | 0,01848 | |
| 30а | 2,26 | 37,21 | 76,54 | 984,87 | 478,78 | 20,39 | 0,01456 | |
| 30б | 2,03 | 35,23 | 79,98 | 1147,8 | 505,61 | 25,01 | 0,01535 | |
| 30с | 1,80 | 33,59 | 83,06 | 1313,0 | 530,97 | 31,75 | 0,01656 | |
| 33а | 2,25 | 41,39 | 88,54 | 1271,7 | 594,43 | 24,29 | 0,01326 | |
| 33б | 2,02 | 39,27 | 92,27 | 1473,2 | 626,93 | 29,92 | 0,01404 | |
| 33с | 1,80 | 37,44 | 95,69 | 1679,8 | 657,23 | 38,04 | 0,01518 | |
| 36а | 2,47 | 92,189 | 49,50 | 104,55 | 1862,2 | 881,77 | 38,91 | 0,01268 |
| 36б | 2,24 | 47,30 | 108,51 | 2123,4 | 925,54 | 46,56 | 0,01329 | |
| 36с | 2,02 | 45,36 | 112,18 | 2390,2 | 966,48 | 57,18 | 0,01417 | |
| 40а | 2,43 | 55,78 | 121,67 | 2655,1 | 1217,2 | 59,74 | 0,01240 | |
| 40б | 2,21 | 53,51 | 125,86 | 2991,7 | 1272,1 | 70,78 | 0,01298 | |
| 40с | 2,00 | 51,51 | 129,80 | 3336,4 | 1324,0 | 85,72 | 0,01378 |
Примечание: При вычислении  приняты
приняты 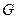 =8∙104 МПа,
=8∙104 МПа,  =2,1∙105 МПа
=2,1∙105 МПа
Таблица 19.3

| Значения моментов инерции 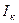 при чистом кручении
прокатных равнобоких уголков (ОСТ 10014-39) при чистом кручении
прокатных равнобоких уголков (ОСТ 10014-39)
| ||||
| Размеры, мм |  , см4 , см4
| Размеры, мм | 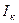 , см4 , см4
| ||
| b | d | b | d | ||
| 0,03330 | 3,277 | ||||
| 0,07680 | 6,333 | ||||
| 0,04230 | 10,83 | ||||
| 0,09813 | 17,01 | ||||
| 0,1195 | 25,12 | ||||
| 0,2292 | 7,667 | ||||
| 0,1408 | 13,13 | ||||
| 0,2708 | 20,67 | ||||
| 0,1621 | 30,58 | ||||
| 0,3125 | 43,16 | ||||
| 0,6328 | 8,333 | ||||
| 0,1835 | 14,28 | ||||
| 0,3542 | 22,49 | ||||
| 0,6048 | 33,31 | ||||
| 0,3958 | 16,59 | ||||
| 0,6768 | 26,15 | ||||
| 0,4792 | 38,78 | ||||
| 0,8208 | 54,82 | ||||
| 1,911 | 74,67 | ||||
| 0,8928 | 31,64 | ||||
| 2,082 | 46,97 | ||||
| 4,000 | 66,48 | ||||
| 1,037 | 52,43 | ||||
| 2,423 | 74,26 | ||||
| 4,667 | 101,3 | ||||
| 7,949 | 173,2 | ||||
| 1,109 | 333,0 | ||||
| 2,594 | 57,89 | ||||
| 5,000 | 112,0 | ||||
| 2,935 | 191,7 | ||||
| 5,667 | 301,5 | ||||
| 9,667 | 200,9 | ||||
| 15,18 |
Таблица 19.4

| Значения моментов инерции 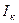 при чистом кручении
прокатных неравнобоких уголков (ОСТ 10014-39) при чистом кручении
прокатных неравнобоких уголков (ОСТ 10014-39)
| ||||||
| Размеры, мм |  , см4 , см4
| Размеры, мм |  , см4 , см4
| ||||
| B | b | d | B | b | d | ||
| 0,04230 | 9,389 | ||||||
| 0,09813 | 3,277 | ||||||
| 0,1088 | 6,333 | ||||||
| 0,2080 | 10,83 | ||||||
| 0,1515 | 3,618 | ||||||
| 0,4968 | 7,000 | ||||||
| 0,3958 | 11,98 | ||||||
| 0,6768 | 18,84 | ||||||
| 1,570 | 8,000 | ||||||
| 0,5000 | 13,71 | ||||||
| 0,8568 | 21,58 | ||||||
| 1,997 | 31,95 | ||||||
| 3,833 | 16,59 | ||||||
| 0,9288 | 26,15 | ||||||
| 2,167 | 38,78 | ||||||
| 4,167 | 17,74 | ||||||
| 1,037 | 27,98 | ||||||
| 2,423 | 41,51 | ||||||
| 4,667 | 19,47 | ||||||
| 2,850 | 45,60 | ||||||
| 5,500 | 64,54 | ||||||
| 88,00 |
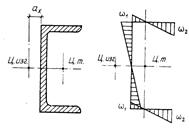
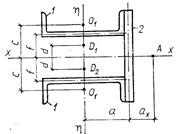
Таблица 19.5. Формулы для вычисления координат центра изгиба и секториальных
моментов инерции некоторых металлических профилей
| Сечение | Координата центра изгиба | Секториальный момент
инерции 
|

| Центр изгиба находится в пересечении осей профиля | |

| 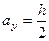
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 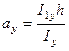
| 
|

| 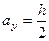
| 
|

| 
| 
|

| 
| 
|

| 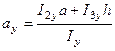
| 
|
| 
| 
|
Примечания:  - центр изгиба профиля;
- центр изгиба профиля;  ,
, 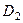 ,
,  - центры изгиба отдельных элементов профиля; 1, 2, 3 – номера элементов, составляющих профиль;
- центры изгиба отдельных элементов профиля; 1, 2, 3 – номера элементов, составляющих профиль;  ,
,  - осевые моменты инерции всего сечения относительно указанных на чертеже осей;
- осевые моменты инерции всего сечения относительно указанных на чертеже осей;  ,
,  ,
,  ,
,  ,
, 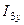 ,
,  - осевые моменты инерции отдельных элементов профиля относительно указанных на чертеже осей: первый индекс – номер элемента, второй – ось;
- осевые моменты инерции отдельных элементов профиля относительно указанных на чертеже осей: первый индекс – номер элемента, второй – ось;  ,
,  ,
,  - секториальные моменты инерции отдельных элементов относительно собственных центров изгиба.
- секториальные моменты инерции отдельных элементов относительно собственных центров изгиба.
Дата добавления: 2015-08-10; просмотров: 585 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Секториальная площадь | | | Общий случай нагружения тонкостенного стержня. Бимомент |