Читайте также:
|
Наиболее целесообразными при кручении являются тонкостенные стержни замкнутого профиля. Геометрическое место точек, равноотстоящих от внешнего и внутреннего контуров поперечного сечения, называется средней линией сечения (рис.19.14).
Наибольшее касательное напряжение в поперечном сечении стержня определяется по формуле
где А ср – площадь сплошного сечения, ограниченного средней линией сечения; t min – минимальная толщина стенки в сечении; Т – внутренний крутящий момент в сечении.
Формула
позволяет вычислить угол закручивания 
стержня длиной l. Интегрирование производится по длине s контура сечения.
Если тонкостенный стержень имеет постоянную толщину стенки t, тогда формула принимает вид
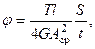
где S – длина контура сечения, отсчитываемая вдоль средней линии сечения.
Дата добавления: 2015-08-10; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Кручение тонкостенных стержней открытого профиля | | | Пример 1. |