Коэффициент полезного действия и удельная работа действительного цикла ГТУ

Задача 1.3. Определить основные показатели эффективно-термодинамического (реального) цикла газотурбинной установки простейшей схемы при следующих исходных данных: начальная температура воздуха на входе в осевой компрессор, t₁ = +15 ⁰C; температура продуктов сгорания на входе в газовую турбину, t₃ = 800 ⁰C; относительный адиабатический КПД осевого компрессора, = 0,85; относительный адиабатический КПД газовой турбины ; приведенная характеристика сети, учитывающая влияние гидравлических сопротивлений, а также различие в средних теплоемкостях рабочего тела в процессах сжатия и расширения, ; потери и служебные расходы воздуха, 1- m =0,05. Сама величина m определяется как отношение количества рабочего тела, проходящего через турбину к количеству рабочего тела, поступившего на сжатие; КПД камеры сгорания = 0,95; степень регенерации, 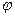= 0,80.

Решение [3]. По уравнению (1.10) определяется соотношение граничных абсолютных температур цикла:

Произведение основных относительных коэффициентов полезного действия, характеризующих отличие реальных процессов от идеальных:

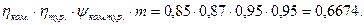
Приведенное (действительное) соотношение граничных абсолютных температур цикла (с учетом необратимых потерь):

Из уравнения (1.11а) определяется характеристика адиабатического расширения, соответствующая условию получения наибольшей удельной работы:

В целях упрощения результатов расчета в качестве рабочего рассматриваемого цикла рассматривает рассматривается сухой воздух.

Графическое отображение зависимости 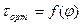приводит к выводу, что при заданной степени регенерации 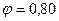характеристика адиабатического расширения в условиях энергетически наивыгоднейшего режима работы ( составит:

Следовательно, средняя абсолютная температура рабочего тела (воздух) в процессе адиабатического расширения может быть определена соотношением:

Соответствующее значение теплоемкости рабочего тела С_рm,тур. = 1,1225 кДж/кг К;

Отсюда следует соотношение граничных давлений расширения по турбине:

Средняя абсолютная температура воздуха в процессе адиабатического сжатия:

Соответствующее значение теплоемкости воздуха в процессе, согласно соответствующим таблицам, составит: С_рm,ком = 1,0529 кДж/кгК.

Характеристика адиабатического сжатия с учетом приведенной характеристики сети составит:

Соответственно, соотношение граничных давлений сжатия (соотношение граничных давлений цикла):

По уравнению (1.9) определяется соотношение мощностей осевого компрессора и газовой турбины в энергетически наивыгоднейшем режиме цикла:

Удельная работа в энергетически наивыгоднейшем режиме:

Конечные абсолютные температуры рабочего тела в процессах расширения и сжатия:

Соотношение разностей температур, характеризующее возможности регенеративного использования тепла:

КПД эффективно-термодинамического цикла простейшего реального газотурбинной установки в условиях энергетически наивыгоднейшего режима работы в итоге составит:

В цикле наибольшей удельной работы средние температуры и основные показатели подсчитываются аналогично.

Результаты расчетов показывают, что в условиях регенеративного использования тепла энергетически наивыгоднейший режим работы имеет несомненные преимущества сравнительно с режимом наибольшей работы, в особенности в эксплуатационной нагрузке установок. Основная характеристика переменного режима работы играет особенно большую роль в стабилизации показателей рабочего процесса на частичных нагрузках и при ухудшении относительных КПД компрессора и газовой турбины.

Задача 1.4. Определить относительный адиабатический КПД осевого компрессора, работающих при следующих исходных данных: степень сжатия по компрессору равна 10; начальная температура процесса сжатия t₁=+15 ⁰C; конечная температура реального процесса сжатия t₂ =340 ⁰C.

При расчетах термодинамических циклов газотурбинных агрегатов с достаточно высокой степенью точности расчетов можно использовать соотношения законов идеальных газов (прежде всего в силу небольших соотношений давлений рабочего тела по тракту установки). При этом условии все параметры рабочего тела определяются только в функции температуры рабочего тела.

Относительный адиабатический КПД компрессора в этом случае определяется как отношение обратимой работы в процессе адиабатического сжатия к реальной работе в пределах заданных температур процесса.

где h_a и h_p – соответственно энтальпия в адиабатическом (обратимом) и реальном процессах сжатия, определяемые только как функции температуры процессов; С_pm и C¹_pm – средние теплоемкости а адиабатическом и реальном процессах сжатия. В силу стабильности теплоемкостей при таких уровнях температур, в расчете их можно принять численно равными; Т_а- конечная температура адиабатического процесса сжатия. Из уравнения адиабаты эта температура определяется соотношением:

Следовательно,

Задача 1.5. В результате проведенного ремонта проточной части газовой турбины (наплавка метала на концы лопаток, установка сотовых уплотнений и т.п.) относительный КПД газовой турбины увеличился на 2,4%, с величины 0,85 до величины 0,87: или на 2,4 %. Определить как это отразилось на изменение КПД и мощности установки в целом.

Решение. При заданных значениях относительных КПД компрессора и газовой турбины, выражение для внутреннего КПД установки записывается в форме (соотношение 1.43):

(а)

При изменении внутреннего относительного КПД турбины на величину , приведенное соотношение принимает вид:

(б)

Сопоставляя между собой соотношения (а) и (б) и принимая во внимание, что при изменении относительного КПД турбины удельный расход топлива по камере сгорания 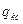практически не изменяется, получим:

(в)

Последнее соотношение получили, разделив числитель и знаменатель на величину и введя в рассмотрение параметр , характеризующий соотношение удельных работ компрессора и газовой турбины, численная величина которого на номинальных режимах работы ГТУ изменяется в диапазоне 0,65-0,70. Следовательно, при , увеличение относительного КПД газовой турбины на 2,4% приведет к увеличению КПД установки в целом примерно на 4%.

Аналогичным соотношением определяется и изменение мощности установки при изменении относительного КПД газовой турбины.

Используя различные численные значения величин, входящих в соотношение (в), можно проследить как будет меняться КПД установки и при других исходных данных.

Задача 1.5. В целях увеличения максимальной удельной работы газотурбинного цикла, в ряде случаев предусматривают двухступенчатую схему сжатия воздуха в осевом компрессоре с использованием промежуточного охлаждения воздуха между ступенями сжатия. Используя положение о том, что температура воздуха на входе во вторую ступень сжатия всегда выше чем в первую, рассмотрим условие оптимальной разбивки общей степени сжатия по осевому компрессору из условия минимума энергетических затрат на процесс сжатия воздуха при следующих исходных данных: общая степень сжатия по компрессору равна 10; температура воздуха на входе в первую ступень сжатия равна Т₁ = 288,2 ⁰К; температура воздуха на входе во вторую ступень сжатия равна Т₂ = 303,2 ⁰К; относительный адиабатический КПД первой ступени сжатия равен 0,88; второй ступени сжатия – 0,84. Требуется определить оптимальную разбивку общей степени на сжатие по первой и второй ступени. Гидравлическими сопротивлениями по циклу ГТУ и холодильнику пренебречь.

Решение. Максимальная удельная работа цикла в этих условиях определяется соотношением (минимальная работа сжатия по компрессору):

,

R – газовая постоянная рабочего тела; m = (k-1)/k – соnst.

Введем в рассмотрение новую независимую переменную .

Тогда в силу условия получим:

;

Переходя к параметру 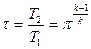и обозначая , получим:

Выполняя общепринятый экстремальный анализ при заданном (постоянной) температуре Т₂ =idem, окончательно получим:

Х_опт. = ; ;

При принятых исходных данных расчета следует, что степень сжатия по первой ступени компрессора должна быть выше чем по второй. По первой степени это составляет примерно 3,74, а по второй 2,66. Хотя при равных численных значениях начальных температур сжатия Т₁ = Т₂ и одинаковых относительных КПД процессов сжатия, степени сжатия по каждому компрессору должны составлять величину порядка 3,16.

Приведенные соотношения позволяют определять оптимальные степени сжатия по ступеням компрессора при самых различных относительных КПД процессов сжатия и различных начальных температурах сжатия.

Однако, в практических условиях, например при последовательной работе нагнетателей газа на компрессорной станции, когда разница в начальных температурах составляет величину порядка 25-28 ⁰С, усложнять систему регулирования режимами двух последовательно работающих агрегатов практического смысла не имеет.

Задача 1.6. Определить мощность, потребляемую осевым компрессором с промежуточным охлаждением воздуха при следующих исходных данных: температура воздуха на входе компрессора t₁ = 20 ⁰C, на выходе компрессора t₂ = 200 ⁰C, секундный расход воздуха через компрессор G_сек.= 65 кг/сек. Расход охлаждающей воды через холодильник G_{в. сек.}= 50 кг/сек, температура воды на входе в холодильник t_в,1= 5 ⁰С, на выходе из холодильника t_в,2 = 28 ⁰С. Относительный КПД осевого компрессора принять равным 0,96; влиянием теплоотдачи через стенки холодильника и гидравлическими потерями потоку пренебречь. Теплоемкость воздуха при определении мощности компрессора принять равной С_р = 1 кДж/кгК; теплоемкость воды при расчете холодильника С_в = 4,19 кДж/кгК.

Решение. Количество тепла снимаемого водой при сжатии воздуха в компрессоре без учета потерь определяется соотношением:

Q = G_в,секС_в (t_в,2 – t_в,1) = 50*4,19 (28 - 5) = 4818,5 кДж/сек = 4818,5 кВт

Мощность, потребляемая осевым компрессором с учетом охлаждения воздуха при сжатии в холодильнике:

Интенсивное охлаждение воздуха при его сжатии в компрессоре может с одной стороны привести к заметному снижению температуры на выходе компрессора, а другой стороны заметно снизить потребляемую компрессором мощность. В нашем примере, например, при степени сжатия = 7, температура воздуха при отсутствии его охлаждения в холодильнике составила бы:

Потребляемая мощность при отсутствии охлаждения и без учета потерь составила бы:

Задача 1.7. Определить основные тепловые и конструктивные показатели трубчатого регенератора газотурбинной установки при следующих исходных данных: расход воздуха и газа в регенераторе G_в = G_г = 85000 кг/час.; давление воздуха за компрессором Р₂ =0,6 МПа; температура воздуха за компрессором и после турбины соответственно t₂ = 250 ⁰C и t₄ = 435 ⁰C. Коэффициент регенерации 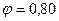; размер трубок 17/20.

Решение. [10]. Температура подогретого воздуха за регенератором составит:

⁰C

Средняя арифметическая температура воздуха в пределах регенератора:

⁰С

Охлаждение продуктов сгорания в регенераторе можно найти из уравнения теплового баланса:

,

где - относительный КПД регенератора, учитывающий тепловые потери с его поверхности, 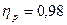; С_рв и С_рг – соответственно средние теплоемкости воздуха и газа в пределах регенератора и определяемые по соответствующим таблицам в функции средней температуры газов. При данных расчета они могут быть приняты на уровне С_рв =1,03 кДж/кгК, а С_рг = 1,05 кДж/кгК. С учетом принятых данных из уравнения теплового баланса следует:

⁰С

t₄¹= t₄ - 148 = 435 -148 = 287 ⁰C

Следовательно, средняя температура продуктов сгорания в регенераторе составит:

⁰C

После ряда прикидочных расчетов, проводимых с целью выбора приемлемых потерь напора в регенераторе, выбирают скорости воздуха и газа по трубкам регенератора. Скорость воздуха в трубках выберем на уровне с_в =23 м/сек; скорость газа на уровне с_г = 18 м/сек.

После проведенных расчетов определяют коэффициенты теплоотдачи со стороны воздуха и продуктов сгорания.

Для определения коэффициента теплоотдачи от стенки к воздуху предварительно определяются необходимые физические константы, входящие в критерии подобия.

Плотность воздуха при принятых исходных данных расчета:

Абсолютная вязкость воздуха определяется по справочным таблицам теории теплопередачи, ; кинематическая вязкость жидкости:

Теплопроводность воздуха также определяется справочным таблицам теории теплопередачи, .

Критерий Рейнольдса,

Re =c_вd/ 23 51245

Re^0,8 = 5857,6

Для воздуха критерий Прандтля можно принять равным, Pr = 0,71.

После чего коэффициент теплоотдачи можно определить по известной формуле М.А. Михеева:

Коэффициент теплоотдачи со стороны продуктов сгорания вычисляется аналогично, с использованием соответствующих формул теплопередачи, однако при этом все физические константы относятся к средней температуре продуктов сгорания, равной 361 ⁰С.

Однако, принимая во внимание, что в продуктах сгорания содержится большое количество воздуха, то коэффициенты теплопроводности и абсолютной вязкости можно определять по данным для воздуха:

Плотность продуктов сгорания за турбиной, принимая давление за ней равным 0,104 МПа, составит:

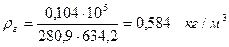
Число Рейнольдса:

Re^0,6 = 199

Коэффициент теплоотдачи от продуктов сгорания к трубкам в первом приближении можно определить по следующему уравнению из теории теплопередачи:

Коэффициент теплопередачи по регенератору можно оценить приближенной формулой:

Поверхность теплопередачи в регенератора после проведенных расчетов можно определить из уравнения теплового баланса, приняв численное значение индекса противоточности на уровне 0,90:

Задача 1.8. На пути отходящих газов ГТУ установлен теплообменник с целью использования тепла отходящих газов для получения горячей воды или пара. Гидравлическое сопротивление теплообменника составляет 300 мм. ртутного столба. Определить на сколько снизится мощность газотурбинной установки при работе теплообменника.

Решение. Численная величина потери мощности ГТУ при установке любого гидравлического сопротивления на выходе продуктов сгорания после газовой турбины определяется соотношения, непосредственно вытекающего из понятия потенциальной работы:

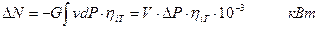
где V – объемный расход продуктов сгорания по турбине, м³/сек; Р падение давления по теплообменнику, Па; - относительный КПД газовой турбины. Так как сопротивление по теплообменнику проще определять в мм. водяного столба, (1 мм. водяного столба 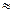10 Па, то введение в расчетное уравнение коэффициента 10^-3 позволяет непосредственно получать искомую величину в кВт. В частности, если расход газов через турбину равен 80 м³/сек, а относительный КПД турбины 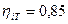, то потеря мощности из-за установки теплообменника составит:

Пример 2.1. Определить параметры потока за решеткой осевого компресса при адиабатическом сжатии, если w₁ = 270 м/сек, Р₁ = 0,1 МПа, t₁=20 ⁰C и w₂ = 200 м/сек. Теплоемкость воздуха с_р = 1,0 кДж/кгК

Решение. После перехода от абсолютных скоростей с к относительным w, из уравнения (2.7) с учетом уравнения (2.9), получаем [19]:

,21=0,21 МПа.

Пример 2.2. Определить скорости потока w₁ и w₂ при отношении давлений Р₂/Р₁ =1,15, углах потока = 30⁰ и = 60⁰ и температуре t₁ =20 ⁰C.

Решение. Из уравнения неразрывности потока, применительно к плоской решетке может быть записано: где - плотность и осевая проекция скорости потока переде решеткой; 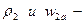то же после решетки. Следовательно, с учетом уравнений Рv^k = idem и 1/v, имеем:

w₂ = 0,565w₁ =0,565*182,6 =103,2 м/сек.

Пример 4.1. Определить мольную массу, элементарный состав газа, а также массовый расход воздуха для окисления 1 кг (1 м³) сжигаемого топлива следующего состава: метан – СН₄ = 94,2%; этан – С₂Н₆ = 2,3%; пропилен – С₃Н₆ = 0,5%; пропан – С₃Н₈ = 1,1 %; азот – N₂ = 1,2%; углекислый газ - СО₂ =0,7%.

Решение. Средняя мольная масса сухого газообразного топлива (m_m) определяетcя из соотношения:

где r_i – мольная (объемная) концентрация отдельных компонентов газообразного топлива в %; m_i – мольная масса различных компонентов топлива.

Элементарный рабочий состав природного газа определяется по соотношениям:

С^р =

где m_i, n_i, q_i - соответственно число атомов углерода, водорода, кислорода и других компонентов топлива. Для данного состава газа элементарный состава газа по каждому компоненту численно будет равен:

; .

Итого 100 %.

Определяется характеристика элементарного состава рабочего топлива, представляющая собой отношение кислорода, необходимого для окисления свободного водорода топлива (Н – 0,126О), к кислороду, необходимому для окисления приведенного углерода топлива (С + 0,375S_л):

Теоретически необходимый расход сухого воздуха в кг. на 1 кг топлива.

L₀ = 0,1154 (1 + E)(C^P + 0,375S^P)= 0,1154(1 + 0,96)73,08= 16,53, (кг/кг)

Плотность газа при стандартных условиях (Р =760 мм.рт. ст. =0,101 МПа; t =20⁰ C; T = 293,15 K):

Относительная плотность газа по воздуху:

Величину L₀ можно найти и по эмпирическому уравнению Вельтера-Бертье-Коновалова, Q_нр. – в ккал/кг:

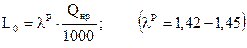
Дата добавления: 2015-07-21