Регрессионный анализ влияния комфортабельности судов на уровень тарифов

Уравнение имеет вид:

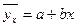, где 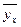= , 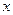= Ккают

Параметры а и b вычислим с помощью решения системы уравнений:

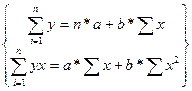, n=16, тогда система принимает вид:

.

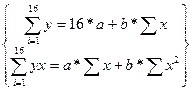Для удобства вычислений расчеты приведем в табличной форме (табл.5), где запишем условия и промежуточные результаты. В этой же таблице поместим данные, которые находятся в дальнейшем при расчете коэффициента корреляции и доверительных границ.

Таблица 5

№ судна	x	y	x2	y2	x*y	Yx	y-Yx	(y-Yx)2
	0,684	89,100	0,468	7938,810	60,944	85,562	3,538	12,520
	0,671	86,900	0,450	7551,610	58,310	84,388	2,512	6,308
	0,844	102,100	0,712	10424,410	86,172	100,001	2,099	4,405
	0,768	84,700	0,590	7174,090	65,050	93,142	-8,442	71,275
	0,735	83,500	0,540	6972,250	61,373	90,164	-6,664	44,413
	0,758	82,300	0,575	6773,290	62,383	92,240	-9,940	98,803
	0,852	102,100	0,726	10424,410	86,989	100,723	1,377	1,895
	0,852	100,500	0,726	10100,250	85,626	100,723	-0,223	0,050
	0,852	107,100	0,726	11470,410	91,249	100,723	6,377	40,663
	0,852	100,500	0,726	10100,250	85,626	100,723	-0,223	0,050
	0,872	105,100	0,760	11046,010	91,647	102,528	2,572	6,614
	0,872	108,100	0,760	11685,610	94,263	102,528	5,572	31,045
	1,074	117,500	1,153	13806,250	126,195	120,758	-3,258	10,616
	0,788	107,400	0,621	11534,760	84,631	94,947	12,453	155,067
	0,852	97,200	0,726	9447,840	82,814	100,723	-3,523	12,413
	0,852	96,500	0,726	9312,250	82,218	100,723	-4,223	17,836
Сумма	13,178	1570,600	10,986	155762,500	1305,492	1570,600	0,000	513,973

Подставим в систему уравнений найденные значения из табл.4: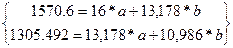

Решив систему уравнений, найдем a и b:

a=23,83; b=90,25

Итак, уравнение регрессии имеет вид:

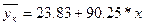, а сама модель в окончательном виде: .

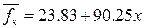Рассчитаем коэффициент корреляции с оценкой тесноты статистической связи между 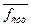и К_кают:

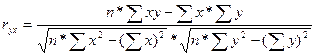
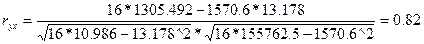
Установим доверительные интервалы вариации тарифной ставки и оценим значимость коэффициента корреляции r_yx.

Доверительные интервалы вариации тарифной ставки определяются из выражения:

,

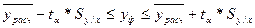где t_α- параметр распределения Стьюдента при ν=n-2 степенях свободы и заданном уровне значимости α. Пусть α=0,05, число степеней свободы ν=16-2=14, табличное значение при этих условиях t ¹⁴_0.05=2,145.

Найдем расчетное значение критерия Стьюдента по нижеприведенной формуле и сравним его с табличным для определения существования статистической связи:

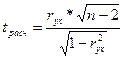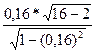= =5,377

Так, как t_расч(5,377)>t_табл(2,145), то статистическая связь существует.

S_y/x- среднеквадратическое отклонение, которое рассчитывается по формуле:

S_y/x = 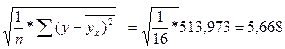долл./сут.

Вычислим доверительные интервалы вариации тарифной ставки с предварительным расчетом среднеквадратического отклонения:

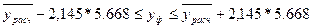
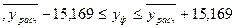или в виде .

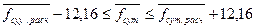Вывод: в результате произведенных расчетов было определено уравнение регрессии, которое имеет вид: 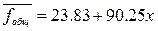. Это уравнение устанавливает взаимосвязь между средневзвешенной суточной тарифной ставкой (у) и коэффициентом общей комфортабельности (х). Между этими показателями существует прямая связь: с возрастанием Кобщ возрастает fcут. Чтобы определить тесноту связи между этими двумя показателями, был рассчитан коэффициент корреляции (его значение равно 0,82, что указывает на прямую связь). Важное значение имеют вычисленные доверительные интервалы, в пределах которых может отклоняться значение fcут от расчетного. Оно может отклоняться в таких пределах: Fсут.расч – 15,169 < Fсут. < Fсут.расч + 15,169

Рассчитав практический параметр Стьюдента и сравнив его с табличным значением при, а = 0,05 и v = 14, получим:

t ¹⁴_0.05= 2,145

t _расч = 5,377

t _расч > t ¹⁴_0.05 - согласно данному методу оценки точности коэффициента корреляции статистическая зависимость существует. Данные расчеты позволяют нам найти средневзвешенную суточную тарифную ставку, зная только значения общей комфортабельности, и интервалы в пределах которых она будет варьироваться.

Дата добавления: 2015-07-20