Логические выражения (логическая функция).

Логическое выражение – это равенство, в левой части которого записано имя функции, а в правой части дано выражение, содержащее двоичные переменные, соединенные знаками логического умножения, сложения и инверсии.

Используются две формы записи:

· ДНФ – дизъюнктивно-нормальная форма, которая представляет собой логическую сумму произведений двоичных переменных:

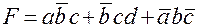
· КНФ – конъюнктивная нормальная форма, логическое произведение логических сумм двоичных переменных.

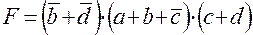
Любая логическая функция может быть представлена в ДНФ или КНФ. При этом может существовать несколько равносильных ДНФ и КНФ.

ДНФ и КНФ форма представления логического выражения, в котором логическая функция может быть записана единственным образом – это:

СДНФ – совершенная ДНФ

СКНФ – совершенная КНФ

Логическое выражение в СДНФ представляет собой логическую сумму минтермов.

Минтерм – это простая конъюнкция, включающая все независимые переменные данной логической функции.

Простая конъюнкция – это логическое проведение, в котором каждая переменная входит один раз в прямом или инверсном виде. Она не должна содержать сумм и отрицаний нескольких переменных.

СКНФ представляет логическое произведение макстермов.

Макстерм – это простая конъюнкция, включающая все независимые переменные данной логической функции.

Простая дизъюнкция – это логическая сумма, в которой каждая переменная входит один раз в прямом либо инверсном виде. Простая дизъюнкция не должна содержать произведений двух и более переменных, либо отрицания суммы нескольких переменных.

Пример 1: логические выражения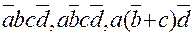

Второе выражение – простая конъюнкция, 1,3 – нет.

Пример 2: даны логические выражения

F₁= 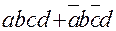- СДНФ выражение

F₂= 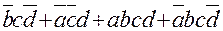- ДНФ выражение.

Дата добавления: 2015-07-20