
Читайте также:
|
Алгебра логики и ее законы применяются для математического исследования цифровых устройств, их синтеза и структурной минимизации.
1. Из определений операций логического сложения и умножения следует:

 а+0=а а·0=0
а+0=а а·0=0
а+1=1 а·1=а
2. Закон нулевого множества:
0· a·b·…·z=0
3. Закон универсального множества
1+a+b+…+z=1
4. Законы тавтологии (идемпотентности, повторения)
a+a=a или a+a+a+….+a=a
a·a=a или a·a·a·…·a=a
5. Переместительный (коммутативный) закон
a+b=b+a a·b=b·a
6. Сочетательный (ассоциативный) закон
(a+b)+c=a+(b+c)=a+b+c
a·b·c=a·(b·c)=a·b·c
7. Распределительный (дистрибутивный) закон
a·(b+c)=ab+ac
a+b·c=(a+b)(a+c)
доказательство: (a+b)(a+c)=aa+ab+ac+bc=a+cb+ac+bc=a(1+b+c)+bc=a+bc
т.к. 1+b+с=1
8. Закон двойного отрицания

9. Правило де Моргана (закон отрицания инверсий)
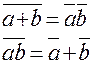
т.е. инверсия дизъюнкции есть конъюнкция инверсий, а инверсия конъюнкции – это дизъюнкция инверсии.
Другая запись правила де Моргана:

Законы отрицания справедливы для любого количества аргументов:

10. Закон поглощения
a+ab=a a(1+b)=a
В, более общем, виде: a+ab+ac+…+az=a.
Также имеет место другая редакция:
a(a+b)=a aa+ab=a+ab=a(1+b)=a
В более общем виде: a(a+b)(a+c)….(a+z)=a
11. Закон склеивания (распространения)
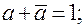

Следствие из данных выражений:

12. Закон деортогонизации
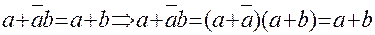
Другая редакция имеет вид:

13. Закон обобщенного поглощения (теория избыточности).
а) Для ДНФ выражений.
Если ДНФ содержит конъюнкцию, которая входит составной частью в другие конъюнкции этого выражения, то последние являются в нем избыточными и могут быть удалены из выражения без изменения значения.

б) Для КНФ выражений
Если КНФ содержит дизъюнкцию, которая входит составной частью в другие дизъюнкции этого выражения, то последние являются в нем избыточными и могут быть удалены из выражения без изменения ее значения.
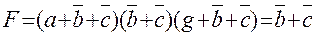
Дата добавления: 2015-07-20; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Логические выражения (логическая функция). | | | Максимальный набор элементарных функций двух переменных. |