
Читайте также:
|
Основными функциями булевой алгебры логики являются логические функции двух переменных F=f(a,b).
Для двух переменных – число возможных комбинаций значений 22 =4, а количество элементарных двоичных функций - 24 =16
| Fi | Название функции | Значение функции | Символ. обознач. | Структурная формула | |
| F0 | Нулевая функция | F0= 0 при любых значениях а и b | F0=
| ||
| F1 | Инверсия а (функция НЕ) | F1={ | 1 при а =0 0 при а =1 | 
| F1=
|
| F2 | Инверсия b (функция НЕ) | F2={ | при b =0 0 при b =1 | 
| F2=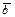
|
| F3 | Дизъюнкция (функция ИЛИ) | F3={ | 0 при а=b =0 1 в ост. случаях | a+b | F3= a+b |
| F4 | Конъюнкция (функция И) | F4={ | 1 при а=b=1 0 в ост. случаях | ab | F4= ab |
| F5 | Повторение а (функция ДА) | F5={ | 1 при а =1 0 при а =0 | a | F5= a |
| F6 | Повторение b (функция ДА) | F6={ | 1 при b =1 0 при b =0 | b | F6= b |
| F7 | Запрет а | F7={ | 0 при а =1 в при а =0 | ba | F7=
|
| F8 | Запрет b | F8={ | 0 при b =1 а при b =0 | ab | F8=
|
| F9 | Штрих Шеффера (функция И-НЕ) | F9={ | 0 при а=b =1 1 в ост. случаях | a/b | F9=
|
| F10 | Стрелка Пирса (функция ИЛИ-НЕ) | F10={ | 1 при а=b =0 0 в ост. случаях | a ¯ b | F10=
|
| F11 | Импликация а | F11={ | 0 при а=0; b=1 1 в ост. случаях | b ® a | F11=
|
| F12 | Импликация b | F12={ | 0 при а =1; b =0 1 в ост. случаях | a ® b | F12=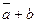
|
| F13 | Неэквивалентность (исключающее ИЛИ) | F13= | 1 при аb | a Å b | F13=
|
| F14 | Равнозначность (эквивалентность) | F14={ | 1 при а = b 0 при аb | a ~ b | F14=
|
| F15 | Единичная функция | F15= | 1 при любых а и b | F15=
|
Дата добавления: 2015-07-20; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные законы и соотношения алгебры логики. | | | Место дисциплины в структуре ООП |