
Читайте также:
|
Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.
Рассмотрим последовательность этого положения (табл. 3.4).
| Вербальная форма | Графическая форма |
| 
|
| 
|
| 
|
| 4. Соединить A2 и В'2; A1и В'1 | 
|
| 5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В'1 = А2В'2 | 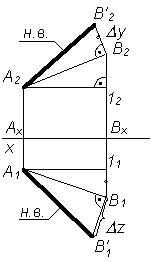
|
 α – угол наклона отрезка АВ к плоскости π1; α – угол наклона отрезка АВ к плоскости π1;
 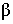 – угол наклона отрезка АВ к плоскости π2 – угол наклона отрезка АВ к плоскости π2
| 
|
При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на π 1, либо на π 2). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка.
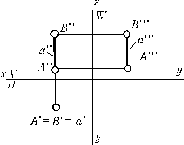
4)Прямые частного положения: линии уровня, проецирующие прямые, конкурирующие точки. Комплексные чертежи кривых линий. Проекция окружности.
Прямые перпендикулярные к какой-либо координатной плоскости называются проецирующими прямыми.
Они делятся на горизонтально-проецирующие, фронтально-конкурирующие, профильно-проецирующие. Проецирующие прямые имеют два важных свойства: во первых они параллельны двум координатным плоскостям и значит на эти плоскости они проецируются в натуральную величину; и второе - на плоскость к которой они перпендикулярны они проецируются в точку (вырождаются в точку, собирают все точки в одну точку), что упрощает решение многих задач встречающихся в начертательной геометрии и, соответственно, в практике задач.
ГОРИЗОНТАЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ

| 
| 
|
ФРОНТАЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ

| 
| 
|
ПРОФИЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ

| 
| 
|
Дата добавления: 2015-07-20; просмотров: 122 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Комплексный чертеж прямой. Прямая общего положения. Определение длины отрезка прямой общего положения способом прямоугольного треугольника. | | | Общие определения и понятия |