Кривые второго порядка

Кривая второго порядка имеет уравнение второй степени в декартовой системе координат. С прямой линией пересекается в двух точках (действительных, совпавших или мнимых).
Эллипс - геометрическое место точек, сумма расстояний которых до двух заданных точек (фокусов) - величина постоянная, равная | 2а | (длине большой оси эллипса). Эллипс не имеет несобственных точек.
Парабола - геометрическое место точек, равноудаленных от данной точки F (фокуса) и данной прямой d (директрисы). Парабола имеет одну несобственную точку.
Гипербола - геометрическое место точек, разность расстояний которых до двух заданных точек (фокусов) - величина постоянная, равная | 2а | (расстоянию между вершинами гиперболы). Гипербола имеет две несобственные точки, по одной на каждой асимптоте.
Кривые второго порядка - эллипс, окружность, парабола и гипербола - могут быть получены при пересечении конуса плоскостью и поэтому называются коническими сечениями.

Пространственные кривые линии

Из закономерных пространственных кривых наибольшее практическое применение находят винтовые линии, в частности, цилиндрическая винтовая линия (рис. 2.2.18).
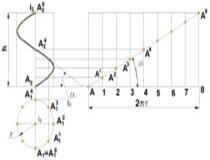Рис 2.2.18

Цилиндрическая винтовая линия представляет собой пространственную кривую, описываемую точкой, совершающей равномерно-поступательное движение по образующей цилиндра вращения, которая в свою очередь вращается вокруг оси цилиндра с постоянной угловой скоростью (рис. 2.2.18). Величина Р, на которую поднимается точка за один оборот образующей, называется шагом винтовой линии.
Горизонтальная проекция винтовой линии является окружностью, а фронтальная - синусоидой. На развертке цилиндрической поверхности винтовая линия изобразится в виде прямой.

Угол называется углом подъема винтовой линии. Этот угол равен углу наклона касательной t в любой точке винтовой линии к плоскости, перпендикулярной ее оси. Цилиндрическая винтовая пиния, подобно прямой и окружности, обладает свойством сдвигаемости.
Свойство сдвигаемости состоит в том, что каждый отрезок линии может сдвигаться вдоль нее, не подвергаясь деформации. Это свойство винтовой линии лежит в основе работы винтовых пар (винт-гайка). Винтовая линия является геодезической на цилиндрической поверхности.

Рис. 2.2.20

Геодезической называется линия, принадлежащая поверхности и кратчайшая из всех линий, которые можно провести между двумя точками поверхности. Кроме цилиндрической винтовой линии, геодезическими линиями также являются прямая на плоскости, окружность большого круга на сфере и др. Геодезическая линия изображается на развертке поверхности в виде прямой линии.
На рис. 2.2.20 показаны примеры применения винтовых линий в технической практике.

Рассмотрим три случая расположения окружности относительно плоскостей проекции.

Случай 1. Окружность m лежит в плоскости  | | П1. Проекция окружности m на П2 – отрезок m2, причем отрезок m2 параллелен оси П2 / П1. На плоскость П1окружность m проецируется в натуральную величину.

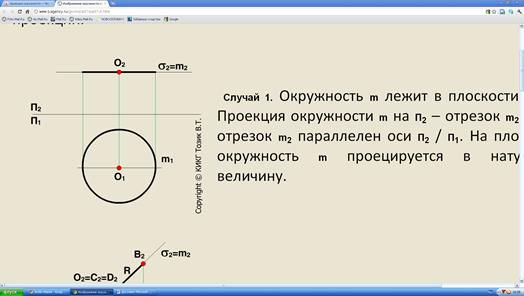
Случай 2. Окружность m лежит в плоскости 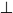 П2. Проекция окружности m на П2 – отрезок m2. Модуль отрезка m2 равен двум радиусам окружности m. Проекция окружности m на П1 – эллипс m1, модуль малой оси которого равен двум радиусам окружности m.

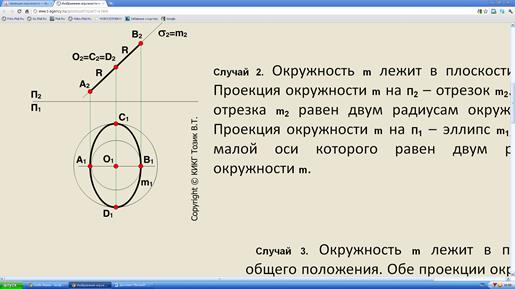
Случай 3. Окружность m лежит в плоскости общего положения. Обе проекции окружности m – эллипсы.

Для построения точек эллипса достаточно знать направление и длины его осей.
Большие оси эллипсов принадлежат линиям уровня, соответственно горизонтали h и фронтали f, длина больших осей равна 2R. Следовательно, большую ось |А1В1| эллипса m1откладываем на h1, |А1В1| = 2R. На П2 ось эллипсаm2 – отрезок M2N2, |M2N2| откладываем на f2, |M2N2| = 2R.
Вторые проекции - |А2В2| и |M1N1| находим из условия принадлежности точек А, В, М и Nфронтали и горизонтали.
Для построения малых осей эллипсов С1D1 иK2L2 (С1D1 перпендикулярно А1В1, K2L2перпендикулярно M2N2) проводим прямую nперпендикулярно большим осям эллипсов: n1перпендикулярно |А1В1|, n2 перпендикулярно|M2N2|.
Для нахождения величины малых полуосей эллипсов проводим ниже описанные построения в обратном порядке. По точкамA1, B1, C1, D1, M1, N1 строим эллипс m1, а по точкам A2, B2, M2, N2, K2, L2 строим эллипс m2.

5)Комплексный чертеж плоскости. Плоскости общего положения, главные линии плоскости. Плоскости частного положения: проецирующие, плоскости уровня.

Комплексный чертеж плоскости – совокупность 2х и более взаимосвязанных ортогональных проекций геометрической фигуры расположенных на одной плоскости, т.е состоящей из комплекса нескольких проекций.

Плоскость – есть множество точек поверхности.

Основные свойства выражают аксиомы:

1. Через 2 точки не лежащей на одной прямой проходит только одна плоскость => плоскость можно задать проекциями 3х точек не лежащей на одной прямой.

2. Прямая проходящая через 2 точки плоскости принадлежит этой плоскости.

Главные линии плоскости:

1. Горизонталь

2. Фронталь

3. Профильная прямые.

Плоскость общего положения -не перпендикулярную и не параллельную плоскостям проекции

Плоскости частного положения:

a) Проецирующая – перпендикулярная к одной из плоскости проекции

b) Плоскость уровня - параллельная одной из плоскости проекции

6)Относительное положение прямыъ: прямые параллельные, пересекаюзиеся, скрещивающиеся. Относительное положение прямой и плоскости, двух плоскостей.

Дата добавления: 2015-07-20