Математическое описание сигналов и операторов систем.

Для анализа САР необходимо иметь ее математическое описание. Система разделяется на элементы, и составляются уравнения, описывающие их поведение (движение) – изменение состояния во времени. Уравнения составляются на основании анализа физических, химических и иных процессов, происходящих в элементах, и применения законов сохранения энергии и вещества, конкретизированных для различных отраслей науки и техники (законы механики, электротехники, гидравлики, теплотехники, оптики и т. д.). Для определения коэффициентов этих уравнений во многих случаях необходимы трудоемкие исследования. Поэтому широко используются также экспериментальные методы для получения математического описания элементов. Такие методы требуют минимальных сведений о процессах, происходящих в элементах, и обеспечивают точность, вполне достаточную для инженерных расчетов.

Ниже будем рассматривать только стационарные САР, у которых свойства элементов не изменяются с течением времени и каждый динамический процесс (изменение состояния элемента во времени) зависит лишь от начального состояния элемента (от начальных условий) и характера внешних воздействий. Предположение о стационарности является идеализацией, ибо не учитывается влияние процесса на свойства элемента, например его старение. Будем предполагать также, что все элементы системы с сосредоточенными параметрами и непрерывного действия. Такие элементы чаще всего описываются дифференциальными уравнениями. Это обыкновенные дифференциальные уравнения с постоянными коэффициентами. В некоторых случаях могут быть алгебраические или интегральные уравнения. Чем точнее описываются процессы в элементе, тем сложнее его уравнение. Поэтому необходим разумный компромисс между наиболее точным описанием элемента и возможностью исследования полученного уравнения.

Если для элемента справедлив принцип суперпозиции, т. е. влияния начальных условий и каждого из внешних воздействий независимы друг от друга, то дифференциальное уравнение элемента оказывается линейным. Однако многие элементы описываются нелинейными дифференциальными уравнениями. Далеко не всякое нелинейное дифференциальное уравнение может быть проинтегрировано и даже отыскание приближенного числового решения может оказаться трудоемким. Поэтому при инженерных расчетах широко используют линеаризацию, т. е. замену нелинейных дифференциальных уравнений приближенными линейными, для которых существует общий метод интегрирования.

В практике весьма широко используют представление элементов их передаточными функциями, что позволяет составлять математические модели систем в виде наглядных структурных схем. Понятие о передаточных функциях и их определение основываются на преобразовании Лапласа. Не менее широко используются временные и частотные характеристики, которые описывают поведение элементов и систем в переходных и установившихся режимах.

Передаточные функции и временные и частотные характеристики составляют тот специфический математический аппарат, который используется линейной теорией автоматического регулирования и управления и позволяет проводить анализ и синтез САР многими методами без интегрирования дифференциальных уравнений и непосредственного исследования из решений. Этот достаточно простой и гибкий математический аппарат весьма удобен для инженерных расчетов, поэтому его используют и в других технических дисциплинах.

Типовые динамические звенья. Понятие, пример.

Пропорциональное (усилительное) звено

Пропорциональным называется звено, поведение которого описывает алгебраическое уравнение

y = ku,

где k - коэффициент усиления. Строго говоря, это звено не является динамическим, но относится к типовым.

Примерами таких звеньев могут служить безынерционные усилители, механические редукторы, многие датчики сигналов и т. д. Передаточная функция звена следующая:

Переходная характеристика (реакция звена на скачкообразное входное воздействие 1(t) имеет вид

Импульсная переходная функция пропорционального звена определяется выражением

Модальные характеристики (собственные значения и собственные векторы) для него отсутствуют.

Заменив в передаточной функции р на получим выражения для частотных характеристик. Амплитудно-фазовая характеристика представляет собой точку на комплексной плоскости в соответствии с формулой

Вещественная частотная характеристика определяется соотношением (рис. 1)

Рис. 1. Вещественная частотная характеристика пропорционального звена

Дифференцирующее звено

Дифференцирующим называется звено, которое описывается дифференциальным уравнением

Его передаточная функция имеет вид

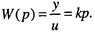
Примером дифференцирующего звена часто может служить тахогенератор постоянного тока. Переходная характеристика дифференцирующего звена определяется выражением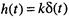

и имеет вид -функции.

Рис. Переходная характеристика звена

Частотные характеристики звена. Амплитудно-фазовая характеристика совпадает с положительной мнимой полуосью комплексной плоскости; вещественная частотная характеристика равна нулю ; мнимая частотная характеристика представляет собой линейно нарастающую функцию . С ней совпадает амплитудная частотная характеристика.

Интегрирующее звено

Интегрирующим называется звено, поведение которого описывает уравнение

Примером интегрирующего звена является операционный усилитель в режиме интегрирования.

Основной динамической характеристикой звена является его дифференциальное уравнение

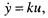
на основе которого можно получить передаточную функцию

Характеристическое уравнение

имеет единственный корень (полюс), р = 0, который представляет собой модальную характеристику интегрирующего звена.

Переходная характеристика звена имеет вид линейно возрастающей функции

Апериодическое звено

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

Различного типа двигатели являются примерами такого звена. Дифференциальное уравнение апериодического звена принято записывать в стандартном виде:

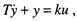
где 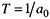- постоянная времени; 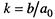- коэффициент усиления звена.

Заменив d/dt на р, перейдем к символической записи дифференциального уравнения

и найдем передаточную функцию апериодического звена:

Для определения модальных характеристик по передаточной функции запишем характеристическое уравнение

Оно имеет единственный корень (полюс),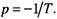

Переходную характеристику звена можно найти как решение уравнения

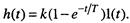
Рис. Переходная характеристика

18. Структурные преобразования систем: последовательное, параллельное.

Для упрощения структурных схем, получения передаточных функций всей разомкнутой системы, передаточных функций замкнутой системы по ошибке и выходному сигналу применяют структурные преобразования. Структурные преобразования основаны на принципе суперпозиции и поэтому применимы только к линейным системам. Они позволяют привести сложную структурную схему к простейшей.

Основные правила преобразования:

1. Последовательное соединение.

Рис. 1

При последовательном соединении структурных звеньев (рис. 1) их эквивалентная передаточная функция будет равна произведению передаточных функций.

2. Параллельное соединение.

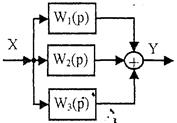
Рис. 2

При параллельном соединении структурных звеньев (рис. 2) их эквивалентная передаточная функция будет равна сумме передаточных функций.

Дата добавления: 2015-07-25