Оценка отношения к риску с помощью безусловного денежного эквивалента

Пусть ЛПР стоит перед выбором из двух альтернатив.

Альтернатива первая – принять решение со средним ожидаемым доходом равным x₀.

Альтернатива вторая – отказаться от рискованного решения и вместо него получить фиксированный доход – x_фикс.

Очевидно, что решение ЛПР будет зависеть от соотношения между x_фикс и x₀, от отношения ЛПР к риску.

Уточним для ЛПР задачу выбора: каким должно быть x_{фик с}, чтобы две альтернативы (риск и фиксированный доход) были равноценны (эквивалентны) с точки зрения ЛПР.

Величина фиксированного дохода, получение которого равноценно для ЛПР его участию в некотором рискованном проекте называется безусловный денежный эквивалент этого проекта:

БДЭ=x_e

Эту величину еще называют детерминированный денежный эквивалент (ДДЭ) или детерминированный денежный доход (ДДД).

Пример 1:

Продается лотерейный билет, по которому можно выиграть 1000 рублей с вероятностью ¼ или выиграть 0 рублей с вероятностью ¾.

За какую максимальную цену вы готовы его купить?

Пример 2:

Вам подарили лотерейный билет из предыдущего примера.

За какую минимальную цену вы готовы его продать?

С точки зрения рационального экономического поведения это должна быть одна и та же величина – безусловный денежный эквивалент лотерейного билета.

Если x_e=x_ож

БДЭ=ОД

ЛПР нейтрален к риску

Если x_e<x_ож

БДЭ<ОД

ЛПР чувствителен к риску

Если x_e>x_ож

БДЭ>ОД

ЛПР склонен к риску

Зная x_e и x_ож можно оценить чувствительность ЛПР к риску.

Чувствительность к риску =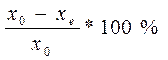

Если эта величина меньше нуля, то ЛРП склонен к риску

Если эта величина равна нулю – нейтрален к риску

Если эта величина больше нуля – чувствителен к риску

Статистические данные показывают, что чувствительность ЛПР к риску изменяется в зависимости от вероятности дохода.

Дата добавления: 2015-07-25