Оценка риска

Рассмотрим еще одну числовую характеристику случайной величины – дисперсию.

Дисперсия равна D(X). Она вычисляется следующим образом:

(3)

(4)

Основные свойства дисперсии:

- D(X)≥0

- D(X)=0 для X=const

Недостатком дисперсии является то, что единица измерения дисперсии равна квадрату единицы измерения случайной величины (рубли меняются на рубли в квадрате, метры на квадратные метры и т. д.)

Поэтому в качестве показателя используют среднее квадратичное отклонение σ(X), равное:

(5)

Как в теории, так и на практике среднее квадратичное отклонение σ(X) чаще всего применяется как мера риска при оценке альтернатив.

Чтобы определить, как зависит уровень риска от величины дисперсии, рассмотрим неравенство Чебышева.

Для любого X с математическим ожиданием m_x=M(X) и дисперсией D_x=D(X) и для любого λ больше нуля справедливо:

(6)

B m_x A

m_x–λ m_x+λ

Неравенству (6) равноценно следующее неравенство:

(7)

Очевидно, что при заданном λ (сумма значимая для ЛПР), ЛПР заинтересован в том, чтобы

Это гарантия того, что полученный доход отклонится от ожидаемого дохода не больше, чем на λ=const.

Чем больше гарантии, тем риск меньше и наоборот, чем меньше гарантии, тем риск больше.

Согласно неравенству (7) данная вероятность убывает при увеличении D_x. Следовательно, чем больше дисперсия случайной величины X, тем труднее гарантировать, что X отклонится от M(X) не больше, чем на величину λ. То есть чем больше дисперсия, тем выше риск.

Рассмотрим теперь влияние величины σ_x на степень риска.

Пусть λ=2*σ_x, тогда

(8)

Пусть λ=3*σ_x, тогда

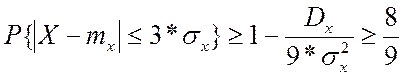(9)

Смысл формул (8) и (9) представим графически:

P≥0.75

m_x–2*σ_x m_x+2*σ_x

То есть, с гарантией 75% X не отклонится от М(X) больше, чем на 2* σ_x

P≥8/9

m_x–3*σ_x m_x+3*σ_x

То есть, с гарантией 89% X не отклонится от М(X) больше, чем на 3* σ_x

Можно сделать вывод, что чем меньше σ_{x ,} тем ближе гарантированные значения X к M(X). Следовательно, чем меньше σ_{x ,} тем риск меньше.

Найдем для нашего примера дисперсию:

D(X₁)=240000

D(X₂)=52500

D(X₃)=0 (D(const)=0)

Найдем σ_x

σ (X₁)=489,9

σ (X₂)=229,129

σ (X₃)=0

С точки зрения рисков самая хорошая альтернатива А₃, далее альтернатива А₂ и самая плохая – альтернатива А₁ (самая рисковая альтернатива).

Для анализа берется σ_{x ,} так как он измеряется в тех же единицах.

Выводы: если для каждой альтернативы могут быть найдены числовые характеристики случайной величины, отражающей целевую функцию ЛПР, то при принятии решения ЛПР может руководствоваться двумя критериями: средний ожидаемый доход (целевая функция), равный математическому ожиданию M(X), или среднее квадратичное отклонение – σ_x – случайной величины X.

Из примера становится очевидным, что во многих случаях критерий ожидаемого дохода и критерий риска противоречат друг другу. Альтернативы, благоприятные с точки зрения ожидаемого дохода часто связаны с высоким риском. Противоречие между средним ожидаемым доходом и стремлением уменьшить риск не снимается полностью, но существуют приемы отбрасывания коэффициентов риска.

---

Дата добавления: 2015-07-25