Кинетика однофотонных необратимых фотохимических реакций

Однофотонной необратимой фотохимической обозначается процесс, описываемый следующей схемой:

	hn

(112)

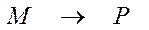
Теперь рассмотрим содержащий фотохимически модифицируемые молекулы М модельный объект объемом V, на который падает пучок монохроматического излучения с интенсивностью J_о. Пусть начальная (до начала воздействия излучения) концентрация молекул М в образце составляет N_o молекул/см³, а к моменту времени t с начала обучения пусть эта концентрация снизится до N молекул/см³. Предположим также, что способностью к поглощению действующего излучения в объекте обладают только немодифицированные молекулы М.

По определению 19 квантовый выход рассматриваемой фотохимической реакции (112) будет равен:

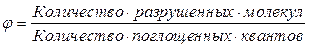
Теперь рассмотрим изменения, происходящие в объекте за время dt.

Концентрация молекул М за это время должна измениться на -dN молекул/см³. Во всем же образце объемом V, таким образом, количество молекул измениться на V´(-dN) молекул. За это же время (dt) на единицу поверхности образца упадет J_о´ dt квантов излучения. На всю же поверхность объекта (S) упадет J_о´ dt´S квантов.

Нас, однако, интересуют не упавшие на объект, а поглощенные им кванты излучения. Поэтому мы применим формулу для расчета поглощенной дозы излучения (5). Она в данном случае будет равна

(113)

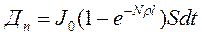
В выражении (113) r - поперечное сечение поглощения молекул М, l – толщина образца.

Подставим выражения для количества разрушенных за время dt молекул и количества поглощенных за это же время квантов излучения в определение квантового выхода j рассматриваемой фотохимической реакции:

(114)

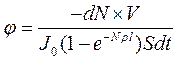
Если предположить, что оптическая плотность объекта для того излучения, которым он облучается, не очень велика (Nrl<<1), можно разложить экспоненту в скобке знаменателя в ряд Тейлора, ограничившись линейным членом разложения:

(115)

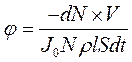
Поскольку объект имеет плоскопараллельную форму, его объем V=Sl, что позволяет упростить выражение (115):

(116)

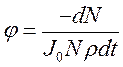
В уравнении (116) 2 переменные, N и t. Разделим их:

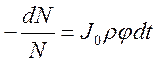
Решим полученное дифференциальное уравнение:

(117)

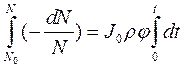
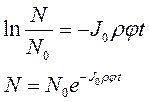
Выражение (117) может быть дополнительно упрощено, если заменить произведение J₀t на дозу облучения (Е), а произведение rj - на параметр s, который принято обозначать, как поперечное сечение фотолиза. Введя эти обозначения, получим окончательный вид уравнения, описывающего зависимость концентрации молекул М в образце от дозы облучения Е:

(118)

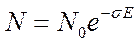
Из выражения (118) следует, что, измерив тем или иным способом зависимость N=f(E) и представив ее в виде ln(N/N₀)=f(E), мы должны получить прямую с коэффициентом пропорциональности между ln(N/N₀) и Е, равным s. Зная величины s и r для молекул М можно рассчитать и квантовый выход анализируемой фотохимической реакции j.

Следует отметить, что при выводе выражения (118) нами было сделано предположение, согласно которому оптическая плотность облучаемого образца, связанная с поглощением света фотолабильными молекулами М, мала. На самом деле такое предположение означает, что вероятность встречи с квантом излучения для молекулы М не зависит от ее локализации в исследуемом объекте. В реальных же условиях такое невозможно – молекулы, локализованные в глубине объекта (дальше от источника излучения), заведомо имеют меньшую вероятность встретиться с квантом излучения и поглотить его, поскольку значительная часть этих квантов уже будет поглощена расположенными ближе к источнику слоями образца.

Для правильного расчета доз излучения, поглощенных оптически плотными объектами Х. Дж. Моровитц в 1950 г. (Morowitz H.J. Absorption effects in volume irradiation of microorganisms. Science, 1950, V. 111, No. 2879, P. 229-230) предложил метод внесения поправки, позволяющей учитывать ослабление интенсивности действующего света по мере его углубления в образец. Было предложено применять при расчете дозы облучения E не падающую на поверхность объекта интенсивность J_о, а интенсивность J^¢, которая связана с падающей интенсивностью J_о через коэффициент k, который зависит от оптической плотности исследуемого объекта на длине волны облучения:

(119)

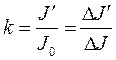
В выражении (119) DJ¢ - ослабление излучения в элементарном объеме образца толщиной dx с учетом поглощения ранее расположенных объемов, а DJ – аналогичное ослабление, но при предположении, что на каждый из элементарных объемов падает излучение с интенсивностью J_о. Соответственно,

	(120)

(121)

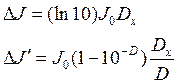
D_x в выражениях (120) и (121) – оптическая плотность элементарного объема, а D – общая оптическая плотность объекта. Из выражений (119) - (121) вытекает, что коэффициент k (называемый коэффициентом Моровитца) может быть рассчитан по формуле:

(122)

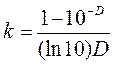
Поскольку мы предположили, что продукты фотомодификации молекулы М света в области облучения не поглощают, а количество исходных молекул М из-за их разрушения под действием излучения по мере увеличения дозы излучения постоянно падает, ясно, что D объекта с ростом дозы будет снижаться. Отсюда вытекает, что и величина коэффициента Моровитца k у образца также будет меняться по мере роста дозы облучения. Поэтому для правильного расчета общей дозы облучения объекта время воздействия излучения на него (t) разбивают на n интервалов величиной Dt каждый. Продолжительность интервала Dt должна быть такой, чтобы в его пределах коэффициент k можно было считать постоянным. Общая доза облучения в таком случае может быть определена по формуле:

(123)

Дата добавления: 2015-07-25