Читайте также:
|
Цель работы:
Экспериментальная проверка расчетных формул для определения величины напряжений, перемещений и направления прогиба консольной балки при косом изгибе.
Общие сведения
Косой изгиб - это такой вид сложного сопротивления, при котором плоскость действия результирующего изгибающего момента в сечении не совпадает ни с одной из главных осей инерции поперечного сечения.
Если поперечное сечение стержня имеет ось симметрии, то она является главной центральной осью. Вторая главная ось инерции проходит через центр тяжести сечения и перпендикулярна первой.
Основной особенностью косого изгиба является несовпадение направления полного прогиба с плоскостью действия результирующего изгибающего момента в заданном сечении. При определении перемещений и напряжений косой изгиб приводится к двум плоским изгибам относительно главных осей инерции сечения.
Экспериментальное определение напряжений и перемещений при косом изгибе производится на консольной балке постоянного прямоугольного сечения.
Если консольная балка нагружена на свободном крае силой P (рис. 1), направление которой не совпадает ни с одной главной осью инерции, то она находится в условиях косого изгиба.
Изгибающие моменты в сечении 1 – 1 (рис. 1) равны
, 
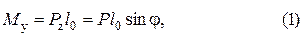
где l 0 – расстояние от точки приложения силы до сечения 1 – 1, в котором установлены тензорезисторы.
Напряжения в местах установки тензорезисторов 1 и 2 (рис. 1) определяются по формулам
, 
где y 1, z 1, y 2, z 2 - координаты точек приложения тензорезисторов 1 и 2.
В формулах (2) знаки перед слагаемыми напряжений взяты из физических соображении по характеру деформаций (плюс – растяжение, минус – сжатие). Координаты точек 1 и 2 приняты по абсолютной величине.
Опытное значение напряжений в точках 1 и 2 определяется методом электротензометрирования. Описание этого метода приведено в главе 3. Для определения напряжений в точках 1 и 2 наклеиваются тензорезисторы (см. рис.1).
Величина полного прогиба при косом изгибе определяется по формуле
где f y и f z – составляющие прогиба в данном сечении по направлению главных осей инерции.
Тогда составляющие прогиба на свободном крае балки определяются по формулам
, 
где j – угол между направлением силы и главной осью инерции сечения y,
l – длина балки, E – модуль Юнга материала балки, Iz, Iy – моменты инерции поперечного сечения относительно главных осей.
Для прямоугольного сечения направление прогибов и линия действия силы Р изображены на рис. 2.
Угол между направлением полного прогиба и осью y определяется из формулы
Порядок выполнения работы
1. Приложить к стержню начальную нагрузку Р 0 и снять показания индикаторов и тензорезисторов.
2. Приложить к образцу нагрузку Р 1= Р 0+D Р и снова снять показания индикаторов и тензорезисторов.
3. Повторить приращение нагрузки до Р 2= Р 0+2D Р и снова снять показания индикаторов и тензорезисторов.
4. Результаты отсчетов по тензорезисторам записать в таблицу (см. форму отчета).
5. Разгрузить установку.
6. Вычислить опытные напряжения по формуле
где K s - цена деления тензорезистора, МПа.
7. Вычислить теоретическое значение нормальных напряжений s в точках 1 и 2 по формулам (2) для силы P =D P.
8. Сравнить расчетные и опытные величины напряжений
9. Вычислить составляющие теоретического прогиба по формулам (4), полный прогиб по формуле (3) и определить угол a по формуле (5) для силы P =D P.
10. Определить полный прогиб f оп и угол aоп по результатам испытаний.
11. Сделать сопоставление теоретических и опытных данных
, 
12. Оформить отчет по прилагаемой форме.
Дата добавления: 2015-07-25; просмотров: 148 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОТЧЕТ 8 | | | Отчет 9 |