При плоском изгибе

Цель работы:

Экспериментальная проверка расчетных формул для определения нормальных и главных напряжений в различных точках поперечного сечения балки при изгибе.

Общие сведения

Изгибу подвергается стальная двутавровая балка, которая закреплена на двух шарнирных опорах и нагружена сосредоточенной силой, приложенной в середине пролета (рис. 1).

На расстоянии а от левой опоры наклеены пять тензорезисторов с первого по пятый, а на такомже расстоянии а от правой опоры наклеены два тензорезистора – шестой и седьмой. Тензорезисторы 1 и 5 наклеены на полках двутавра на оси симметрии; тензорезисторы 2 и 4 наклеены на стенке двутавра параллельно продольной оси x на расстоянии y ₂ = у ₄ от нейтральной оси; тензорезисторы 3, 6 и 7 наклеены на оси x, причем тензорезистор 3 параллелен оси x, а тензорезисторы 6 и 7 расположены под углом 45^o к оси.

Нормальные напряжения в поперечном сечении балки при плоском изгибе определяются по формуле

где M - изгибающий момент в анализируемом сечении балки; I_z - осевой момент инерции относительно нейтральной оси z; у - расстояние от нейтральной оси z до точки, в которой определяется напряжение.

Знак напряжений определяется по характеру деформации (см. рис. 1)

Главные напряжения при прямом поперечном изгибе определяются по формуле

В точках, расположенных на нейтральной оси, нормальные напряжения равны нулю σ = 0, поэтому

где Q - поперечная сила в рассматриваемом сечении, (S_z ^отс)_max - статический момент инерции площади поперечного сечения относительно поперечной оси z, расположенной выше (ниже) нейтральной оси x, b – ширина поперечного сечения балки в том месте балки на уровне y, где наклеен тензорезистор.

Главные напряжения в нейтральном слое действуют на площадках, наклоненных к оси x под углом 45⁰. Знак касательных, а значит и главных напряжений в точке установки тензорезисторов 6 и 7, определяется по знаку поперечной силы (рис. 1). Направление касательных и главных напряжений показано на рис. 2.

Величины опытных напряжений в точках 1, 2, 3, 4 и 5 определяются по закону Гука для линейного напряженного состояния:

где e _i - продольная деформация в i точке сечения, Е - модуль Юнга, Δ n_i - приращение показаний прибора для i точки сечения, К _s - цена деления прибора, МПа.

В центральном слое балки наблюдается чистый сдвиг, так как в нем отсутствуют нормальные напряжения. Поэтому главные напряжения в точках 6 и 7 определяются по формулам для плоского напряженного состояния

(5)

Порядок выполнения работы

1. Установить номер исследуемого двутавра. Замерить расстояние а (рис. 1).

2. Снять начальные показания прибора в точках i =1,2,3…7при нагрузке P ₀ = 0 (рис. 1). Результаты измерений занести в табл.1 (см. форму отчета).

3. Последовательно увеличивая нагрузку ступенями Δ P найти приращения показания Δ n_i как разницу между последующими и предыдущими показаниями прибора

.

Результаты вычислений занести в тaбл.1 (см. форму отчета). При этом необходимо соблюдать условие

,

где σ_пц - предел пропорциональности материала, для малоуглеродистой стали σ_пц = 200 МПа, W_z - осевой момент сопротивления сечения балки.

4.Вычислить опытную величину напряжений для точек 1, 2, 3, 4 и 5 по формуле (4), для точек 6 и 7 - по формулам (5), подставляя вместо Δ n_i среднеарифметическое значение Δ n_i нескольких измерений.

5. Определить теоретическое значение напряжения в точках 1, 2, 3, 4 и 5 по формуле (1), в точках 6 и 7 - по формуле (3) на ступень нагрузки Δ Р, используя эпюры Q и M (см. рис. 1). Построить эпюры σ,полученные теоретическим и опытным путем в сечении балки.

6. Найти расхождение между теоретическими и опытными значениями напряжений в процентах:

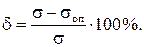
Результаты вычислений занести в табл. 2 (см. форму отчета).

7. Отчет оформить по прилагаемой форме.

Дата добавления: 2015-07-25