Растяжение стального образца с измерением упругих деформаций

Цель работы:

Экспериментальная проверка закона Гука при растяжении. Определение модуля Юнга и коэффициента Пуассона стали.

Общие сведения

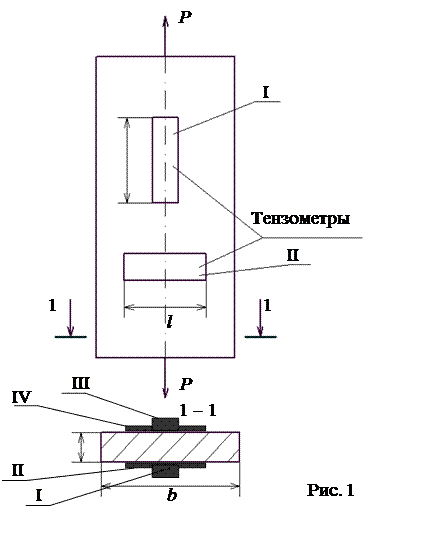В работе подвергается испытанию на растяжение плоский стальной

образец в пределах упругих деформаций. На образце (рис. 1) установлены два продольных и два поперечных тензометра.

Для измерения деформаций образца в работе используется электротензометрический метод, изложенный в главе 3.

1. Проверка закона Гука

P

Опытная проверка закона Гука при растяжении производится на основе экспериментально определенной диаграммы растяжения (рис.2), которая строится по результатам испытаний.

Рис. 2

Справедливость закона Гука устанавливается наличием на диаграмме прямолинейного участка.

2. Определение модуля Юнга материала

Модуль Юнга материала определяется по формуле закона Гука

где Δ Р – ступень нагрузки, l – база тензометра продольной деформации, А – площадь поперечного сечения образца, Δ l – абсолютное удлинение образца на отрезке длиной l.

Зная среднее приращение отсчетов Δ n _1cp электротензометра продольной деформации (из таблицы наблюдений) и цену деления прибора в относительной деформации на одно деление K _e, можно вычислить относительную продольную деформацию образца

Цена деления прибора – электротензометра устанавливается опытным путем (см. главу 3).

Подставляя в формулу (1) данные опыта (2), получим

3. Определение коэффициента Пуассона

Коэффициентом Пуассона или коэффициентом поперечной деформации называется отношение относительной поперечной деформации к относительной продольной деформации, взятое по модулю

где m – коэффициент Пуассона, e – относительная продольная деформация, e¢ – относительная поперечная деформация.

Относительная поперечная деформация образца вычисляется по формуле

где Δ n _2cp – среднее приращение отсчетов электротензометра поперечной деформации (берется из таблицы наблюдений), K _e¢ – цена деления электротензометра поперечной деформации.

Если характеристики (база, цена деления) тензометров продольной и поперечной деформации одинаковы, то величина коэффициента Пуассона определяется по формуле

Дата добавления: 2015-07-25