Математическая модель САР

Для того чтобы проанализировать данную систему необходимо составить ее математическую модель. Каждый элемент системы описывается некоторым уравнением. Это уравнение характеризует работу данного элемента. Точность математического описания системы определяется требуемой точностью регулирования. Чем точнее мы будем описывать элементы системы, тем сложнее получится математическая модель. Поэтому, необходимо найти разумный компромисс между точностью описания системы и сложностью ее математической модели.

Будем предполагать, что САР температуры воздуха является стационарной. Предположение о том, что все элементы системы с сосредоточенными параметрами и непрерывны во времени позволяет использовать для описания элементов системы обыкновенные дифференциальные уравнения с постоянными коэффициентами.

Так как многие элементы могут описываться нелинейными дифференциальными уравнениями, то решить их бывает сложно. Поэтому для описания системы применяется приближенная линеаризованная модель, в терминах передаточных функций.

Динамика элементов САР описывается следующей системой уравнений:

Т₀ 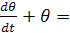k₀q (t-τ) + k_в θ_а – объект регулирования;

Т_д + U= k_дθ – датчик температуры;

ΔU=U₀-U – сравнивающий орган;

U_y=k_yU_y – электронный усилитель;

X= k₃U_y- заслонка и электромагнит без учета электромеханических переходных процессов;

q=k_фХ- форсунка.

Параметры – T₀ T_д и k₀ k_в k_д k_y k₃ k_ф соответственно постоянные времени и передаточные коеффициенты, τ- время запаздывания.

Дата добавления: 2015-07-25