Элементы квантовой статистики

Фазовое пространство. Функция распределения. Рассмотрим систему из N частиц. Свяжем с ней многомерное пространство всех координат и импульсов частиц системы. Состояние системы определяется заданием переменных 6 N, так как состояние каждой частицы определяется тройкой координат x, y, z и тройкой проекций импульса , , . Поэтому размерность многомерного пространства равно 6 N. Это пространство называется фазовым пространством. Каждому микросостоянию системы в классическом случае отвечает точка в фазовом пространстве. При квазиклассическом описании движения системы на каждое квантовое состояние системы приходится в этом пространстве элементарный объем .

При взаимодействии с окружающей средой состояние системы меняется. Вероятность dP некоторого состояния системы (p, q) можно представить с помощью функции распределения

(8)
Здесь означает произведение дифференциалов координат и импульсов всех частиц. По определению функции распределения

,
где интегрирование производится по всему фазовому пространству.

При известной функции распределения можно определить макроскопические параметры системы. Любой макроскопический параметр L в смысле статистической физики является средним по микросостояниям

. (9)

Явное выражение функции распределения для системы, находящейся в тепловом контакте с большим тепловым резервуаром было получено Гиббсом. Оно называется каноническим распределением Гиббса и имеет вид

,
где A – нормировочная постоянная, n – совокупность квантовых чисел, определяющих данное состояние.

Статистика Бозе-Эйнштейна и Ферми-Дирака. Наиболее простым объектом для изучения является идеальный газ. Реальный газ можно считать идеальным, если взаимодействие частиц несущественно. Состояние системы невзаимодействующих тождественных частиц можно характеризовать с помощью чисел заполнения , определяющих среднее число частиц в i -м квантовом состоянии.

Для систем частиц, образованных бозонами, числа заполнения могут принимать любые целые неотрицательные значения: 0, 1, 2, …. Для систем, образованных фермионами, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения равна числу частиц системы. С помощью канонического (или большого канонического) распределения Гиббса можно определить числа заполнения квантовых состояний.

Числа заполнения идеального газа бозонов – бозе-газа – определяются соотношением

. (10)
Это выражение называется распределением Бозе-Эйнштейна. Здесь – среднее число бозонов в квантовом состоянии с энергией , m – параметр, который называется химическим потенциалом. Его величина определяется из условия , где N – число частиц в системе. Химический потенциал по своему определению является функцией числа частиц и температуры .

Распределение фермионов по энергиям имеет вид

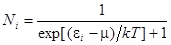. (11)
Смысл входящих в (11) величин тот же, что и в (10). Распределение (11) называется распределением Ферми-Дирака.

Если , то распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана

, (12)
где . Таким образом, при малых числах заполнения () оба квантовых газа ведут себя подобно классическому газу.

Квантовый газ называется вырожденным, если числа заполнения сравнимы с единицей или больше ее (последнее возможно для бозе-газа). Вырожденный бозе-газ и ферми-газ существенно отличаются друг от друга и в свою очередь от идеального газа. Так в вырожденном бозе-газе при понижении температуры происходит бозе-конденса­ция, когда на нижний энергетический уровень переходит большое число частиц. Бозе-конденсацией объясняются такие явления как сверхтекучесть и сверхпроводимость.

Вырождение газов наступает при понижении температуры и/или повышении плотности газа. В качестве параметра вырождения квантового газа используется температура , при которой . Эта характеристическая температура называется температурой вырождения.

Дата добавления: 2015-07-25