Читайте также:
|
Уравнение плоскости, проходящей через данную точку, имеет вид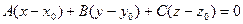 
.
Подставим в указанное уравнение координаты точки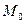 
. Получим: 
.
Условие перпендикулярности плоскости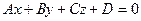 
и прямой 
имеет вид
(3.13)
Так как искомая плоскость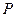 
перпендикулярна прямой 
, то в качестве нормального вектора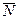 
плоскости можно взять направляющий вектор 
прямой , т.е. в формуле (3.13) отношение 
можно принять равным единице. Следовательно, уравнение плоскости 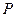примет вид 
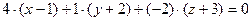. Запишем это уравнение в общем виде: 
.
12) Составить канонические уравнения прямой , проходящей через точку 
перпендикулярно плоскости :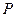 
.
Дата добавления: 2015-07-25; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Решение. |