Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Решение. Уравнение плоскости, проходящей через точки , , имеет вид:

Задача №1. | Решение. | Решение. | Решение. | Решение. | Решение. | Решение. | Решение. | Решение. |


Читайте также:
  1. Будь любезен, подумай хорошо, прежде чем принимать решение. Я не намерен терпеть твои перепады настроения и все такое. У меня, в конце концов, может не выдержать сердце.
  2. Глава 21. Решение.
  3. Задача 3. Дифференциальные уравнения с разделяющимися переменными. Найти общее решение.
  4. И тогда, Мудрейший отец, глава клана, принял решение. Он решил отправиться туда, где еще сохранились чистокровные фаэны. В Атлантиду.
  5. Принимаем осознанное решение.
  6. Решение.
  7. Решение.

Уравнение плоскости, проходящей через точки , , 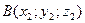имеет вид:

(3.7)

Тогда уравнение плоскости в силу уравнения (3.7) имеет вид или .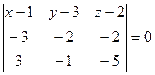

Запишем полученное уравнение в общем виде, т.е. в виде 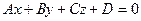. Для этого раскроем определитель по первой строке . После преобразований получим: .

2) Найти нормальный вектор плоскости .

Дата добавления: 2015-07-25; просмотров: 42 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Решение.| Решение.
mybiblioteka.su - 2015-2025 год. (0.005 сек.)