
Читайте также:
|
5.1. Комплексная амплитуда гармонического сигнала

Комплексная амплитуда является комплексным числом (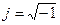 - мнимая единица), определяется только амплитудой и начальной фазой сигнала и не зависит от его частоты.
- мнимая единица), определяется только амплитудой и начальной фазой сигнала и не зависит от его частоты.
Комплексная амплитуда обозначается тем же символом, что и амплитуда сигнала, но с точкой сверху (в литературе используются и другие маркирующие отметки, например, горизонтальная черта сверху символа).
Например, если мгновенное значение гармонического напряжения равно 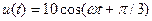 В, то его комплексная амплитуда имеет вид
В, то его комплексная амплитуда имеет вид 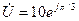 В или
В или 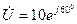 В.
В.
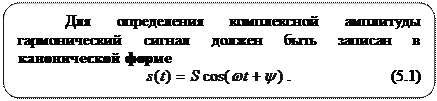
Если запись сигнала отличается от формы (5.1) то необходимо провести соответствующие тригонометрические преобразования, представленные в табл. 5.1.
Таблица 5.1
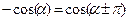
| 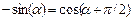
| 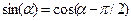
|
Если гармоническое напряжение имеет вид 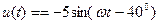 мВ, то после преобразования получим
мВ, то после преобразования получим 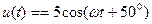 мВ, а комплексная амплитуда будет равна
мВ, а комплексная амплитуда будет равна 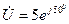 мВ.
мВ.
5.2. Операции с комплексными числами
Комплексные числа могут быть записаны в двух формах: алгебраической и показательной.
В алгебраической форме комплексное число 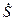 записывается в виде
записывается в виде
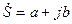 , (5.2)
, (5.2)
где 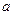 - действительная, а
- действительная, а 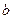 - мнимая части комплексного числа,
- мнимая части комплексного числа, 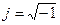 .
.
В показательной форме комплексное число представляется выражением
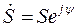 , (5.3)
, (5.3)
величину 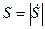 называют модулем, а
называют модулем, а 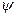 - аргументом комплексного числа.
- аргументом комплексного числа.
От алгебраической формы можно перейти к показательной, модуль комплексного числа равен
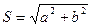 , (5.4)
, (5.4)
а аргумент
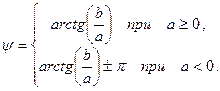 (5.5)
(5.5)
Аргумент комплексного числа, как и начальная фаза гармонического сигнала (подраздел 2.2), величина многозначная, к ней можно добавить (или вычесть) 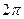 любое число раз. Для обеспечения однозначности аргумента комплексного числа его значения выбирают в диапазоне, например, от
любое число раз. Для обеспечения однозначности аргумента комплексного числа его значения выбирают в диапазоне, например, от 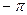 до
до 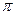 или от 0 до
или от 0 до 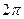 .
.
Показательную форму комплексного числа можно заменить алгебраической с помощью соотношений
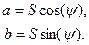 (5.6)
(5.6)
Они вытекают из известной в математике формулы Эйлера,
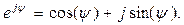 (5.7)
(5.7)
Например, если комплексное число в алгебраической форме равно 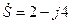 , то в показательной форме его можно записать в виде
, то в показательной форме его можно записать в виде
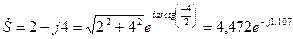 .
.
Если комплексное число равно 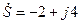 , то в показательной форме получим
, то в показательной форме получим
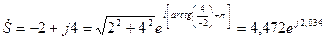 .
.
Для комплексного числа в показательной форме в виде 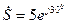 его алгебраическая форма имеет вид
его алгебраическая форма имеет вид
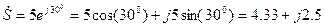 .
.
С комплексными числами проводятся все четыре арифметические действия.
При сложении и вычитании комплексных чисел 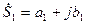 и
и 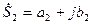 в алгебраической форме получим
в алгебраической форме получим
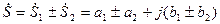 . (5.8)
. (5.8)
Если числа заданы в показательной форме, то перед сложением или вычитанием их необходимо преобразовать в алгебраическую форму.
Операции умножения и деления удобнее выполнять в показательной форме, когда 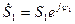 и
и 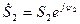 , при этом при умножении комплексных чисел их модули перемножаются, а аргументы складываются,
, при этом при умножении комплексных чисел их модули перемножаются, а аргументы складываются,
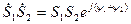 , (5.9)
, (5.9)
а при делении делятся модули и вычитаются аргументы,
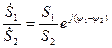 . (5.10)
. (5.10)
Умножение можно провести и с алгебраической формой сомножителей по известным правилам с учетом того, что 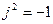 ,
,
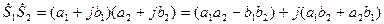 . (5.11)
. (5.11)
При делении комплексных чисел в алгебраической форме используется операция устранения комплексности в знаменателе путем умножения числителя и знаменателя дроби на число, комплексно сопряженное знаменателю. Для заданного числа 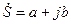 комплексно сопряженное число
комплексно сопряженное число 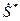
равно 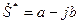 , то есть отличается от
, то есть отличается от 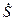 противоположным знаком при мнимой части. Произведение двух комплексно сопряженных чисел всегда равно квадрату их модуля,
противоположным знаком при мнимой части. Произведение двух комплексно сопряженных чисел всегда равно квадрату их модуля,
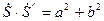 . (5.12)
. (5.12)
Тогда при делении в алгебраической форме получим
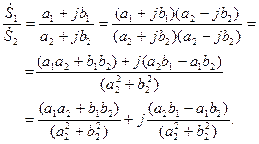 (5.13)
(5.13)
Рассмотрим пример 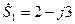 и
и 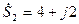 , тогда
, тогда
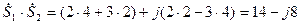 ,
,
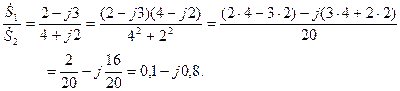
Эти операции можно провести и в показательной форме, тогда
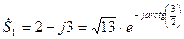 ,
,
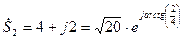 ,
,
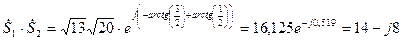 ,
,
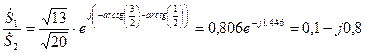 .
.
Как видно, полученные результаты совпадают.
Полезно запомнить следующие равенства, вытекающие из формулы Эйлера (5.7),
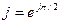
| 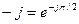
| 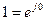
| 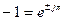
|
Вычисления с комплексными числами удобно проводить на персональной ЭВМ с помощью пакета программ MathCAD.
5.3. Законы Ома и Кирхгофа для комплексных амплитуд
токов и напряжений
Законы Ома и Кирхгофа применимы в своих классических формулировках для комплексных амплитуд токов и напряжений.

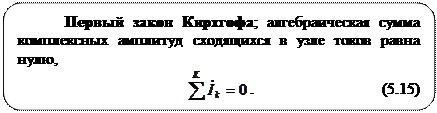

Знаки в алгебраических суммах определяются выбранными положительными направлениями токов и напряжений и направлением обхода контура.
5.4. Комплексные сопротивления и проводимости
элементов цепи
Значения комплексных сопротивлений 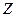 и проводимостей
и проводимостей 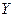 элементов цепи R, L и C приведены в табл. 5.2 (запомните эти формулы).
элементов цепи R, L и C приведены в табл. 5.2 (запомните эти формулы).
Таблица 5.2
| R | L | C | |
Комплексное
сопротивление 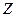
| 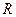
| 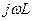
| 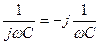
|
Комплексная проводимость 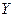
| 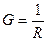
| 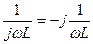
| 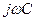
|
Комплексные сопротивление и проводимость сопротивления 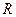 всегда действительны (мнимая часть равна нулю), а индуктивности и емкости – мнимые (действительная часть равна нулю).
всегда действительны (мнимая часть равна нулю), а индуктивности и емкости – мнимые (действительная часть равна нулю).
Для комплексного сопротивления 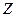 из закона Ома (5.14) можно записать
из закона Ома (5.14) можно записать
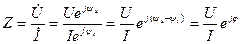 , (5.17)
, (5.17)
где 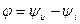 - сдвиг фаз между напряжением и током в элементе. Для сопротивления
- сдвиг фаз между напряжением и током в элементе. Для сопротивления 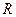 напряжение и ток совпадают по фазе, то есть
напряжение и ток совпадают по фазе, то есть 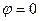 и из (5.17) величина
и из (5.17) величина 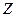 действительна.
действительна.
В индуктивности напряжение опережает по фазе ток на 900 (на 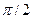 радиан), следовательно
радиан), следовательно 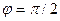 , тогда
, тогда 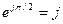 и величина комплексного сопротивления индуктивности
и величина комплексного сопротивления индуктивности 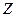 оказывается с нулевой действительной и положительной мнимой частями. В емкости
оказывается с нулевой действительной и положительной мнимой частями. В емкости 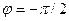 ,
, 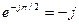 и ее комплексное сопротивление имеет нулевую действительную и отрицательную мнимую части.
и ее комплексное сопротивление имеет нулевую действительную и отрицательную мнимую части.
Аналогичный анализ проводимости элементов цепи проведите самостоятельно.
5.5. Комплексные сопротивление и проводимость
участка цепи
Полные комплексные сопротивления (и проводимости) двухполюсного участка цепи с произвольным соединением элементов определяются по тем же правилам, что и для цепи постоянного тока:
- комплексное сопротивление последовательного соединения двухполюсников равно сумме их комплексных сопротивлений;
- комплексная проводимость параллельного соединения двухполюсников равна сумме их комплексных проводимостей.
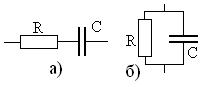 Например, сопротивление последовательной цепи, показанной на рис. 5.1а при
Например, сопротивление последовательной цепи, показанной на рис. 5.1а при 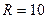 кОм и
кОм и 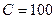 пФ на частоте
пФ на частоте 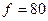 кГц равно
кГц равно 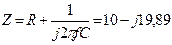 кОм,
кОм,
а проводимость параллельной Рис. 5.1.
цепи на рис 5.1б -
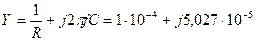 Сим.
Сим.
Зная комплексное сопротивление цепи, можно определить ее комплексную проводимость и наоборот,
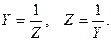 (5.18)
(5.18)
Например, для последовательной цепи на рис. 5.1а ее проводимость равна
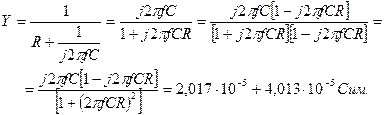
Расчет проведен методом устранения комплексности знаменателя путем умножения числителя и знаменателя дроби на множитель, комплексно-сопряженный знаменателю.
Можно провести вычисление проводимости путем преобразования комплексного сопротивления из алгебраической формы в показательную,
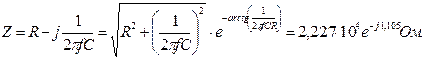 .
.
Тогда для проводимости получим
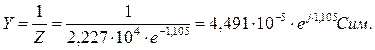
 |
Комплексное сопротивление цепи со смешанным соединением элементов определяется следующим образом:
- в цепи выделяется фрагмент с простым (последовательным или параллельным) соединением элементов и определяется его сопротивление или проводимость;
- фрагмент заменяется эквивалентным элементом, в полученной цепи вновь выделяется простой фрагмент и повторяется предыдущее действие;
- эти действия повторяются до тех пор, пока цепь не трансформируется в один элемент с соответствующим сопротивлением или проводимостью.
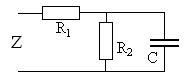 Рассмотрим цепь, схема которой показана на рис. 5.2 при
Рассмотрим цепь, схема которой показана на рис. 5.2 при 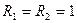 кОм,
кОм, 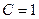 нФ,
нФ, 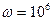 рад/с и определим ее комплексное сопротивление
рад/с и определим ее комплексное сопротивление 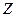 . В цепи выделяется простой параллельный фрагмент из элементов
. В цепи выделяется простой параллельный фрагмент из элементов
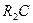 и определяется его сопро-
и определяется его сопро-
тивление 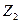 , равное Рис. 5.2
, равное Рис. 5.2
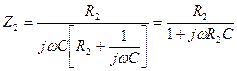 .
.
Тогда параллельный фрагмент 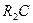 заменяется эквивалентным элементом с сопротивлением
заменяется эквивалентным элементом с сопротивлением 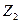 и схема цепи принимает вид, показанный на рис. 5.3.
и схема цепи принимает вид, показанный на рис. 5.3.
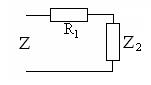 Для полученной последовательной цепи ее сопротивление
Для полученной последовательной цепи ее сопротивление 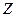 равно
равно
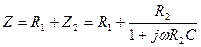 .
.
.
Подставляя исходные данные, получим Рис. 5.3
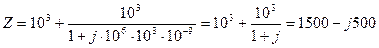 Ом.
Ом.
5.6. Характеристики комплексного сопротивления
и проводимости
Полное комплексное сопротивление 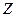 в показательной форме можно записать в виде
в показательной форме можно записать в виде
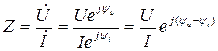 . (5.19)
. (5.19)
Модуль комплексного сопротивления равен отношению амплитуд (действующих значений) напряжения и тока,
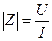 . (5.20)
. (5.20)
Аргумент комплексного сопротивления равен сдвигу фаз между напряжением и током,
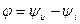 , (5.21)
, (5.21)
Комплексная проводимость в показательной форме имеет вид
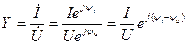 , (5.22)
, (5.22)
ее модуль равен отношению амплитуд (действующих значений) тока и напряжения,
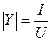 , (5.23)
, (5.23)
а аргумент – сдвигу фаз между током и напряжением,
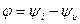 . (5.24)
. (5.24)
Таким образом, комплексное сопротивление и проводимость характеризуют взаимосвязь амплитуд и начальных фаз напряжения и тока.
Представим комплексное сопротивление в алгебраической форме,
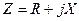 , (5.25)
, (5.25)
где 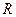 - активная а,
- активная а, 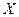 - реактивная составляющие комплексного сопротивления. Все величины в (5.25) измеряются в Омах.
- реактивная составляющие комплексного сопротивления. Все величины в (5.25) измеряются в Омах.
Рассмотрим в качестве примера сопротивление цепи, показанной на рис. 5.2.
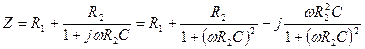 . (5.26)
. (5.26)
Как видно, активная 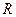 составляющая сопротивления
составляющая сопротивления 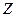 равна
равна
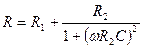 , (5.27)
, (5.27)
а реактивная 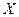 -
-
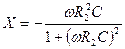 , (5.28)
, (5.28)
и обе зависят от частоты сигнала.
Зависимости от частоты 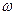 активной
активной 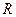 и реактивной
и реактивной 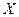 составляющих сопротивления для цепи рис. 5.2 показаны на рис. 5.4. На низких частотах
составляющих сопротивления для цепи рис. 5.2 показаны на рис. 5.4. На низких частотах 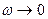 емкость является разрывом цепи и сопротивление
емкость является разрывом цепи и сопротивление 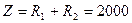 Ом. На высоких частотах
Ом. На высоких частотах 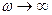 емкость представляет собой короткое замыкание (ее сопротивление стремится к нулю) и сопротивление цепи равно
емкость представляет собой короткое замыкание (ее сопротивление стремится к нулю) и сопротивление цепи равно 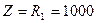 Ом. И в том и другом случаях реактивное сопротивление стремится к нулю.
Ом. И в том и другом случаях реактивное сопротивление стремится к нулю.
При 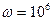 рад/с получается ранее вычисленное значение
рад/с получается ранее вычисленное значение 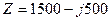 Ом.
Ом.
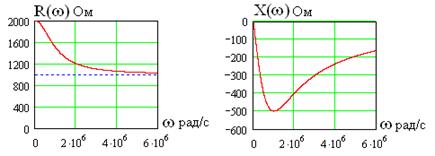
Рис. 5.4.
Аналогичный анализ проводимости цепи, показанной на рис. 5.2, проведите самостоятельно.
5.7. Комплексная мощность

Это комплексная величина с действительной и мнимой частями,
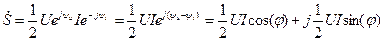 . (5.30)
. (5.30)
Комплексная мощность измеряется в ВА (вольт-амперах).
Как видно, действительная (активная) составляющая
комплексной мощности представляет собой среднюю мощность 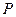 , потребляемую двухполюсником,
, потребляемую двухполюсником,
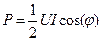 . (5.31)
. (5.31)
Как уже отмечалось, активная мощность измеряется в ваттах.
Мнимая (реактивная) составляющая 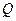 комплексной мощности равна
комплексной мощности равна
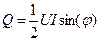 (5.32)
(5.32)
и характеризует процессы накопления и обмена энергией с источником в реактивных элементах цепи. Эта мощность не расходуется цепью и измеряется в ВАр (вольт-амперы реактивные), она численно равна максимальной скорости запасания энергии в цепи. Реактивная мощность может быть положительной (при 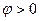 ), при этом энергия запасается в магнитном поле индуктивностей, или отрицательной (при
), при этом энергия запасается в магнитном поле индуктивностей, или отрицательной (при 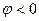 ) при накоплении энергии в электрическом поле емкостных элементов.
) при накоплении энергии в электрическом поле емкостных элементов.
Модуль комплексной мощности равен
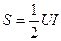 (5.33)
(5.33)
и измеряется в ВА. Величину 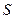 называют полной мощностью, она определяется активной и реактивной мощностями,
называют полной мощностью, она определяется активной и реактивной мощностями,
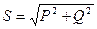 . (5.34)
. (5.34)
Можно записать
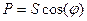 , (5.35)
, (5.35)
величину 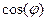 называют коэффициентом мощности. При
называют коэффициентом мощности. При 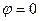 потребляемая мощность
потребляемая мощность 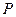 максимальна и равна полной мощности
максимальна и равна полной мощности 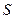 , а реактивная мощность
, а реактивная мощность 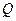 равна нулю.
равна нулю.
Если для вычисления мощности используются действующие значения напряжения и тока, то в приведенных соотношениях удаляется множитель 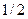 .
.
5.8. Расчет мощности, потребляемой двухполюсником
Зная комплексные амплитуды напряжения и тока, согласно (5.29), можно определить комплексную мощность, например, при 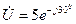 В и
В и 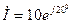 А получим, что сдвиг фаз между напряжением и током равен
А получим, что сдвиг фаз между напряжением и током равен 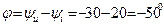 . Тогда комплексная мощность равна
. Тогда комплексная мощность равна
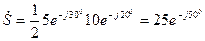 ВА,
ВА,
активная составляющая (потребляемая мощность) -
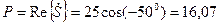 Вт,
Вт,
реактивная мощность –
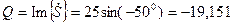 ВАр,
ВАр,
а полная мощность -
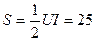 ВА.
ВА.
Отрицательная реактивная мощность свидетельствует о том, что цепь накапливает энергию в емкостном элементе. Так как коэффициент мощности равен 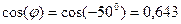 , то потребляемая мощность существенно меньше полной.
, то потребляемая мощность существенно меньше полной.
Мощности можно определить, зная комплексную амплитуду напряжения (или тока) и комплексное сопротивление (проводимость) цепи.
 Рассмотрим цепь на рис. 5.2 с подключенным к ней идеальным источником гармонического напряжения
Рассмотрим цепь на рис. 5.2 с подключенным к ней идеальным источником гармонического напряжения 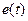 , показанную на рис. 5.5.при
, показанную на рис. 5.5.при 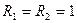 кОм,
кОм, 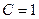 нФ,
нФ, 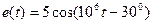 В. Ком-
В. Ком-
плексная амплитуда 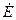 ЭДС Рис. 5.5
ЭДС Рис. 5.5
источника равна 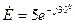 В,
В,
а комплексное сопротивление цепи было определено ранее,
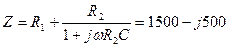 Ом.
Ом.
По закону Ома найдем комплексную амплитуду тока 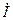 ,
,
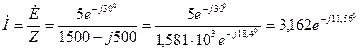 мА,
мА,
а полная комплексная мощность равна
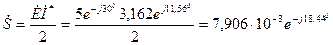 ВА,
ВА,
или в алгебраической форме
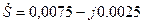 ВА.
ВА.
Таким образом, потребляемая цепью мощность равна 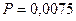 Вт, реактивная мощность -
Вт, реактивная мощность - 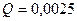 ВАр, а полная мощность -
ВАр, а полная мощность - 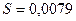 ВА.
ВА.
На практике наибольший интерес представляет определение мощности, которую потребляет цепь от одного или нескольких источников. Необходимо помнить, что в электрической цепи мощность потребляется только активными элементами – сопротивлениями.
Потребляемую мощность в цепи, содержащей несколько сопротивлений, можно определить, если известны амплитуды (действующие значения) токов или напряжений на этих элементах.

Расчет токов и напряжений на элементах цепи будет рассмотрен в дальнейшем.
В цепи с комплексным сопротивлением 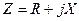 при протекании через нее тока с амплитудой
при протекании через нее тока с амплитудой 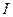 потребляемая мощность равна
потребляемая мощность равна
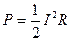 . (5.36)
. (5.36)
Аналогично в цепи с комплексной проводимостью 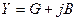 при наличии на ней напряжения с амплитудой
при наличии на ней напряжения с амплитудой 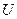 потребляемая мощность будет равна
потребляемая мощность будет равна
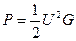 . (5.37)
. (5.37)
5.9. Максимизация потребляемой мощности
В инженерной практике часто возникает необходимость обеспечить максимум активной мощности, передаваемой от источника сигнала в нагрузку.
В качестве примеров можно выделить задачу максимизации мощности на валу электродвигателя при питании его от силовой сети. Аналогичная проблема возникает при передаче высокочастотной мощности от выходного усилителя радиопередатчика в антенну для излучения электромагнитных волн (высокочастотная мощность стоит очень дорого как с экономической, так и с технической точки зрения).
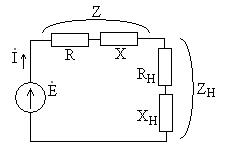 Схема электрической цепи показана на рис. 5.6. В цепь включен реальный источник напряжения с комплексной амплитудой ЭДС
Схема электрической цепи показана на рис. 5.6. В цепь включен реальный источник напряжения с комплексной амплитудой ЭДС 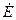 и внутренним комплексным сопротивлением
и внутренним комплексным сопротивлением 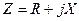 , к которому подключена нагрузка с комплексным сопротивлением
, к которому подключена нагрузка с комплексным сопротивлением 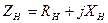 .
.
Необходимо подоб- Рис. 5.6.
Рать такое сопротивление
нагрузки, при котором она потребляла бы от источника максимальную мощность.
Комплексная амплитуда тока в цепи 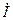 равна
равна
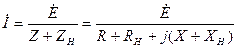 ,
,
тогда для амплитуды тока получим
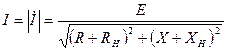 , (5.38)
, (5.38)
в выражение для потребляемой мощности примет вид
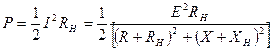 , (5.39)
, (5.39)
так как мощность потребляется только в активном сопротивлении 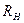 .
.
Необходимо определить максимум (5.39) по двум независимым переменным – активному 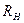 и реактивному
и реактивному 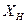 сопротивлениям нагрузки. Как видно, величина
сопротивлениям нагрузки. Как видно, величина 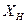 присутствует только в знаменателе дроби и сумма
присутствует только в знаменателе дроби и сумма 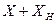 возводится в квадрат. Минимум знаменателя будет иметь место при условии
возводится в квадрат. Минимум знаменателя будет иметь место при условии
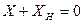 или
или 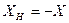 . (5.40)
. (5.40)
Таким образом, реактивное сопротивление нагрузки должно быть по модулю равно реактивному сопротивлению источника и иметь противоположный характер (если у источника сопротивление индуктивно, то у нагрузки оно должно быть емкостным и наоборот). В результате получим
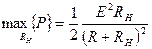 . (5.41)
. (5.41)
Максимум (5.41) по 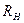 можно найти, вычислив производную этой функции и приравняв ее нулю. В результате получим (проделайте это самостоятельно) условия, при которых
можно найти, вычислив производную этой функции и приравняв ее нулю. В результате получим (проделайте это самостоятельно) условия, при которых
потребляемая нагрузкой мощность максимальна,
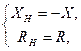 (5.42)
(5.42)
и соответствующую величину мощности
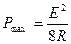 . (5.43)
. (5.43)
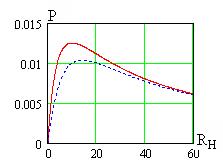 Зависимости мощности в нагрузке
Зависимости мощности в нагрузке 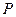 от
от 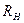 при
при 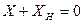 (сплошная линия) и
(сплошная линия) и 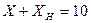 Ом (пунктирная линия) показаны на рис. 5.7 при
Ом (пунктирная линия) показаны на рис. 5.7 при 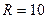 Ом и
Ом и 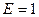 В.
В.
Как видно, при отклонении от оптимальных условий (5.42) потребляемая нагрузкой мощность замет но снижается. Рис. 5.7
Рассмотрим коэффи-
циент полезного действия (КПД) – отношение мощности в нагрузке к мощности, потребляемой от источника сигнала, при условии (5.40) равной
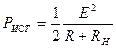 . (5.44)
. (5.44)
тогда КПД 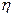 равен
равен
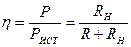 . (5.45)
. (5.45)
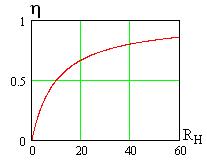 Зависимость КПД от активной составляющей сопротивления нагрузки показана на рис. 5.8. Как видно, при условии передачи максимума мощности в нагрузку КПД равен 0,5 (50%), то есть половина мощности источника потребляется его же внутренним со-
Зависимость КПД от активной составляющей сопротивления нагрузки показана на рис. 5.8. Как видно, при условии передачи максимума мощности в нагрузку КПД равен 0,5 (50%), то есть половина мощности источника потребляется его же внутренним со-
Рис. 5.8 противлением (происходит на-
грев источника). При повышении 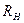 КПД увеличивается, однако при этом снижается мощность, передаваемая в нагрузку.
КПД увеличивается, однако при этом снижается мощность, передаваемая в нагрузку.
5.10. Задания для самостоятельного решения
Задание 5.1. Определите комплексные амплитуды гармонических сигналов
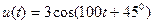 В,
В, 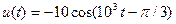 мВ
мВ
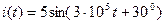 мА,
мА, 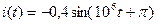 А.
А.
Задание 5.2. По заданной комплексной амплитуде определите мгновенные значения сигналов, их амплитуды и начальные фазы
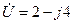 В,
В, 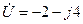 мВ,
мВ, 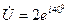 В,
В, 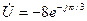 мВ,
мВ,
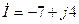 мА,
мА, 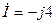 А,
А, 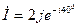 мА,
мА, 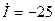 мкА.
мкА.
Задание 5.3. Вычислите сумму, разность, произведение и частное комплексных чисел 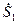 и
и 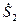 , результаты запишите в алгебраической и показательной формах.
, результаты запишите в алгебраической и показательной формах.
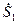
| 4-j3 | 7-j4 | -j | 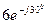
| 20+j3 | 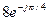
| |
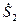
| -8+j2 | -j5 | j | -1-j | 5+j2 | 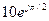
| 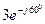
|
Задание 5.4. Для чисел из задания 5.3 вычислите их модуль и аргумент, а также обратную величину 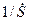 .
.
Задание 5.5. Найдите полное комплексное сопротивление 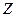 и проводимость
и проводимость 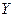 показанных на рис. 5.9 цепей при
показанных на рис. 5.9 цепей при 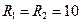 кОм,
кОм, 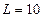 мГн и
мГн и 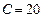 пФ на частоте
пФ на частоте 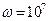 рад/c.
рад/c.
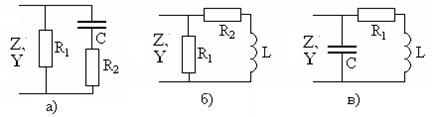
Рис. 5.9
Задание 5.6. Получите общие формулы для полного комплексного сопротивления цепей из задания 5.5. Найдите формулы его модуля, аргумента, активной и реактивной составляющих, постройте их графики в зависимости от частоты сигнала.
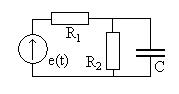
Задание 5.7. Вычислите мощность, потребляемую показанной на рис.5.10 цепью при ЭДС источника 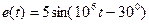 В,
В,
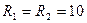 кОм и
кОм и 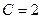 нФ. Рис. 5.10
нФ. Рис. 5.10
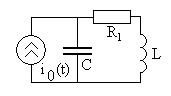
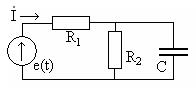
Задание 5.8. Определите мощность, потребляемую показанной на рисунке цепью от источника тока 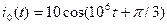 мА при
мА при 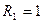 кОм,
кОм, 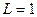 мГн и
мГн и 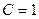 нФ.
нФ.
Рис. 5.11
Дата добавления: 2015-07-25; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В ЛИНЕЙНЫХ ЦЕПЯХ | | | НАПРЯЖЕНИЙ В ЛИНЕЙНОЙ ЦЕПИ |