
|
Читайте также: |
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют постоянные напряжения и протекают постоянные токи, то модели реактивных элементов L и C существенно упрощаются.
Модель сопротивления 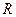 остается прежней и связь между напряжением
остается прежней и связь между напряжением 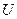 и током
и током 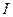 определяется законом Ома в виде
определяется законом Ома в виде
 . (3.1)
. (3.1)
В идеальной индуктивности мгновенные значения напряжения и тока связаны соотношением
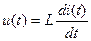 . (3.2)
. (3.2)

Аналогично в емкости связь между мгновенными значениями напряжения и тока определяется в виде
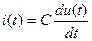 . (3.3)
. (3.3)

Таким образом, в модели цепи постоянного тока присутствуют только сопротивления (модели резисторов) и источники сигнала, а реактивные элементы (индуктивности и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала. Он предполагает вычисление сопротивлений участков цепи, для которых известна величина тока (или напряжения), с последующим определением неизвестного напряжения (или тока). Рассмотрим пример расчета цепи, схема которой приведена на рис. 3.1, при токе идеального источника  А и сопротивлениях
А и сопротивлениях 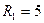 Ом,
Ом,  Ом,
Ом,  Ом. Необходимо определить токи ветвей
Ом. Необходимо определить токи ветвей  и
и 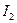 , а также напряжения на сопротивлениях
, а также напряжения на сопротивлениях  ,
,  и
и 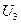 .
.
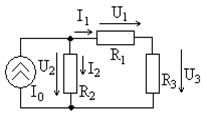 Известен ток источника
Известен ток источника  , тогда можно вычислить сопротивление цепи
, тогда можно вычислить сопротивление цепи 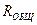 относительно зажимов источника тока (параллельного соединения сопротивления
относительно зажимов источника тока (параллельного соединения сопротивления  и последовательно соединен-
и последовательно соединен-
Рис. 3.1. ных сопротивлений  и
и  ),
),
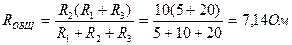 .
.
Тогда напряжение  на источнике тока (на сопротивлении
на источнике тока (на сопротивлении  ) равно
) равно
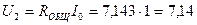 В.
В.
Затем можно найти токи ветвей
 А,
А,
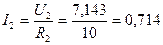 А.
А.
Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде  . Подставляя вычисленные значения, получим
. Подставляя вычисленные значения, получим  А, что совпадает с величиной тока источника.
А, что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина  уже найдена)
уже найдена)
 В,
В,
 В.
В.
По второму закону Кирхгофа  . Складывая полученные результаты, убеждаемся в его выполнении.
. Складывая полученные результаты, убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе законов Ома
и Кирхгофа
Общий метод расчета токов и напряжений в электрической цепи на основе законов Ома и Кирхгофа пригоден для расчета сложных цепей с несколькими источниками сигнала.
Расчет начинается с задания обозначений и положительных направлений токов и напряжений для каждого элемента (сопротивления) цепи.
Система уравнений включает в себя подсистему компонентных уравнений, связывающих по закону Ома токи и напряжения в каждом элементе (сопротивлении) и подсистему
топологических уравнений, построенную на основе первого и второго законов Кирхгофа.
Рассмотрим расчет простой цепи из предыдущего примера, показанной на рис. 3.1, при тех же исходных данных.
Подсистема компонентных уравнений имеет вид
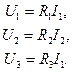 (3.4)
(3.4)
В цепи имеется два узла (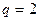 ) и две ветви, не содержащие идеальных источников тока (
) и две ветви, не содержащие идеальных источников тока (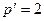 ). Следовательно, необходимо записать одно уравнение (
). Следовательно, необходимо записать одно уравнение ( ) по первому закону Кирхгофа,
) по первому закону Кирхгофа,
 , (3.5)
, (3.5)
и одно уравнение второго закона Кирхгофа ( ),
),
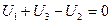 , (3.6)
, (3.6)
которые и образуют подсистему топологических уравнений.
Уравнения (3.4)-(3.6) являются полной системой уравнений цепи. Подставляя (3.4) в (3.6), получим
 , (3.7)
, (3.7)
а, объединив (3.5) и (3.7), получим два уравнения с двумя неизвестными токами ветвей,
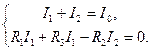 (3.8)
(3.8)
Выражая из первого уравнения (3.8) ток  и подставляя его во второе, найдем значение тока
и подставляя его во второе, найдем значение тока  ,
,
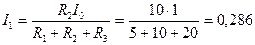 А, (3.9)
А, (3.9)
а затем найдем 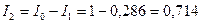 А. По вычисленным токам ветвей из компонентных уравнений (3.4) определим напряжения. Результаты расчета совпадают с полученными ранее в подразделе 3.2.
А. По вычисленным токам ветвей из компонентных уравнений (3.4) определим напряжения. Результаты расчета совпадают с полученными ранее в подразделе 3.2.
Рассмотрим более сложный пример расчета цепи в схеме, показанной на рис. 3.2, с параметрами 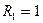 Ом,
Ом, 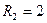 Ом,
Ом, 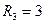 Ом,
Ом, 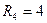 Ом,
Ом,  Ом,
Ом, 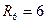 Ом,
Ом,
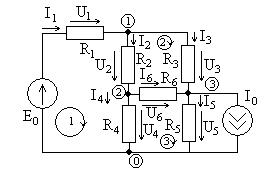
 В,
В,  А.
А.
Цепь содержит  узла (их номера указаны в кружках) и
узла (их номера указаны в кружках) и  ветвей, не содержащих идеальные источники тока. Система компонентных уравнений цепи имеет вид
ветвей, не содержащих идеальные источники тока. Система компонентных уравнений цепи имеет вид
Рис. 3.2
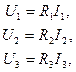
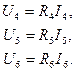 (3.10)
(3.10)
По первому закону Кирхгофа необходимо записать 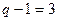 уравнения (узел 0 не используется),
уравнения (узел 0 не используется),
 (3.11)
(3.11)
По второму закону Кирхгофа составляется 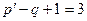 уравнения для трех независимых контуров, отмеченных на схеме окружностями со стрелками (внутри указаны номера контуров),
уравнения для трех независимых контуров, отмеченных на схеме окружностями со стрелками (внутри указаны номера контуров),
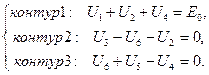 (3.12)
(3.12)
Подставляя (3.11) в (3.13), совместно с (3.12) получим систему шести  уравнений вида
уравнений вида
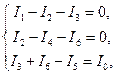 (3.13)
(3.13)

Из второго и третьего уравнений выразим
 (3.14)
(3.14)
а из первого  , тогда подставив
, тогда подставив 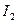 и
и  , получим
, получим  . Подставляя токи
. Подставляя токи  ,
, 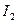 и
и  в уравнения второго закона Кирхгофа, запишем систему из трех уравнений
в уравнения второго закона Кирхгофа, запишем систему из трех уравнений
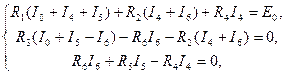
которую после приведения подобных запишем в виде
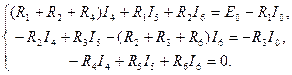 (3.15)
(3.15)
Обозначим
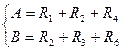 , (3.16)
, (3.16)
и из третьего уравнения системы (3.15) запишем
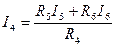 . (3.17)
. (3.17)
Подставляя полученное значение 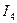 в первые два уравнения (3.15), получим систему из двух уравнений вида
в первые два уравнения (3.15), получим систему из двух уравнений вида
 (3.18)
(3.18)
Из второго уравнения (3.18) получим
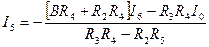 , (3.19)
, (3.19)
тогда из первого уравнения найдем ток 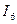
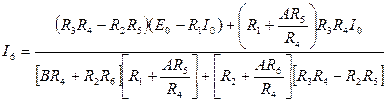 . (3.20)
. (3.20)
Вычислив 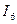 , из (3.19) найдем
, из (3.19) найдем 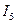 , из (3.17) вычислим
, из (3.17) вычислим 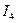 , а затем из уравнений подстановки найдем токи
, а затем из уравнений подстановки найдем токи  ,
, 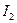 ,
, 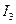 .
.
Как видно, аналитические вычисления достаточно громоздки, и для численных расчетов целесообразней использовать современные программные пакеты, например, MathCAD2001. Пример программы показан на рис. 3.3.
Матрица - столбец  содержит значения токов
содержит значения токов  А,
А,  А,
А, 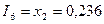 А. Остальные
А. Остальные
токи вычисляются согласно уравнениям (3.14) и равны
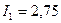 А,
А, 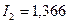 А,
А,  А. Вычисленные значения токов совпадают с полученными по приведенным выше формулам.
А. Вычисленные значения токов совпадают с полученными по приведенным выше формулам.
Общий метод расчета цепи по уравнениям Кирхгофа приводит к необходимости решения  линейных алгебраических уравнений. При большом числе ветвей
линейных алгебраических уравнений. При большом числе ветвей  возникают математические и вычислительные трудности. Это означает, что целесообразно искать методы расчета, требующие составления и решения меньшего числа уравнений.
возникают математические и вычислительные трудности. Это означает, что целесообразно искать методы расчета, требующие составления и решения меньшего числа уравнений.

Рис. 3.3
3.4. Метод контурных токов
Метод контурных токов базируется науравнениях второго закона Кирхгофа и приводит к необходимости решения  уравнений,
уравнений,  - число всех ветвей, в том числе и содержащих идеальные источники тока.
- число всех ветвей, в том числе и содержащих идеальные источники тока.
В цепи выбираются  независимых контуров и для каждого
независимых контуров и для каждого 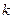 -го из них вводится кольцевой (замкнутый) контурный ток
-го из них вводится кольцевой (замкнутый) контурный ток  (двойная индексация позволяет отличать кон-
(двойная индексация позволяет отличать кон-
турные токи от токов ветвей). Через контурные токи можно выразить все токи ветвей и для каждого независимого контура записать уравнения второго закона Кирхгофа. Система уравнений содержит  уравнений, из которых определяются все контурные токи. По найденным контурным токам находятся токи или напряжения ветвей (элементов).
уравнений, из которых определяются все контурные токи. По найденным контурным токам находятся токи или напряжения ветвей (элементов).
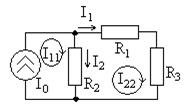 Рассмотрим пример цепи на рис. 3.1. На рис 3.4 приведена схема с указанием обозначений и положительных направлений двух контурных токов
Рассмотрим пример цепи на рис. 3.1. На рис 3.4 приведена схема с указанием обозначений и положительных направлений двух контурных токов  и
и  (
( ,
, 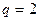 ,
, 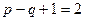 ).
).
Рис. 3.4 Через ветвь 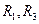 проте-
проте-
кает только контурный ток  и его направление совпадает с
и его направление совпадает с  , поэтому ток ветви
, поэтому ток ветви  равен
равен
 . (3.21)
. (3.21)
В ветви  протекают два контурных тока, ток
протекают два контурных тока, ток  совпадает по направлению с
совпадает по направлению с 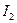 , а ток
, а ток  имеет противоположное направление, следовательно
имеет противоположное направление, следовательно
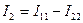 . (3.22)
. (3.22)
Для контуров, не содержащих идеальные источники тока, составляем уравнения второго закона Кирхгофа с использованием закона Ома, в данном примере записывается одно уравнение
 . (3.23)
. (3.23)
Если в контур включен идеальный источник тока, то для него
уравнение второго закона Кирхгофа не составляется, а его контурный ток равен току источника с учетом их положительных направлений, в рассматриваемом случае
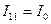 . (3.24)
. (3.24)
Тогда система уравнений принимает вид
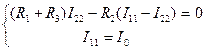 . (3.25)
. (3.25)
В результате подстановки второго уравнения в первое получим
 , (3.26)
, (3.26)
тогда ток  равен
равен
 А, (3.27)
А, (3.27)
а ток 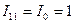 А. Из (3.21)
А. Из (3.21)  А, а из (3.22) соответственно
А, а из (3.22) соответственно 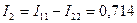 А, что полностью совпадает с полученными ранее результатами. При необходимости по найденным значениям токов ветвей по закону Ома можно вычислить напряжения на элементах цепи.
А, что полностью совпадает с полученными ранее результатами. При необходимости по найденным значениям токов ветвей по закону Ома можно вычислить напряжения на элементах цепи.
Рассмотрим более сложный пример цепи на рис. 3.2, схема которой с заданными контурными токами показана на рис. 3.5. В этом случае число ветвей 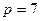 , количество узлов
, количество узлов  , тогда число независимых контуров и уравнений по методу контурных токов равно
, тогда число независимых контуров и уравнений по методу контурных токов равно  . Для токов ветвей можно записать
. Для токов ветвей можно записать
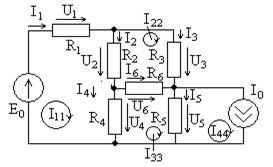
Рис. 3.5
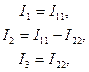 (3.28)
(3.28)
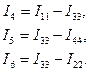
Первые три контура не содержат идеальных источников тока, тогда с учетом (3.28) и использованием закона Ома для них можно записать уравнения второго закона Кирхгофа,
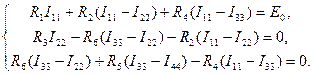 (3.29)
(3.29)
В четвертом контуре присутствует идеальный источник тока, поэтому для него уравнение второго закона Кирхгофа не составляется, а контурный ток равен току источника (они совпадают по направлению),
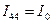 . (3.30)
. (3.30)
Подставляя (3.30) в систему (3.29), после преобразования получим три уравнения для контурных токов в виде
 (3.31)
(3.31)
Систему уравнений (3.31) можно решить аналитически (например, методом подстановки – проделайте это), получив формулы для контурных токов, а затем из (3.28) определить токи ветвей. Для численных расчетов удобно использовать пакет программ MathCAD, пример программы показан на рис. 3.6. Результаты вычислений совпадают с расчетами, приведенными на рис. 3.3. Как видно, метод контурных токов требует составления и решения меньшего числа уравнений по сравнению с общим методом расчета по уравнениям Кирхгофа.

Рис. 3.6
3.5. Метод узловых напряжений
Метод узловых напряжений базируется на первом законе Кирхгофа, при этом число уравнений равно  .
.
В цепи выделяются все 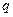 узлов и один из них выбирается в качестве базисного, которому присваивается нулевой потенциал. Потенциалы (напряжения)
узлов и один из них выбирается в качестве базисного, которому присваивается нулевой потенциал. Потенциалы (напряжения) 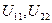 …
… 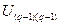 остальных
остальных  узлов отсчитываются от базисного, их положительные направления обычно выбираются стрелкой в базисный узел. Через узловые напряжения с использованием закона Ома и второго закона Кирхгофа выражаются токи всех ветвей
узлов отсчитываются от базисного, их положительные направления обычно выбираются стрелкой в базисный узел. Через узловые напряжения с использованием закона Ома и второго закона Кирхгофа выражаются токи всех ветвей
и для  узлов записываются уравнения первого закона Кирхгофа.
узлов записываются уравнения первого закона Кирхгофа.
 Рассмотрим пример цепи, показанной на рис. 3.1, для метода узловых напряжений ее схема показана на рис. 3.7. Нижний узел обозначен как базисный (для этого используется символ «земля» - точка нулевого потенциала), напряжение верхнего узла относительно базисного обо-
Рассмотрим пример цепи, показанной на рис. 3.1, для метода узловых напряжений ее схема показана на рис. 3.7. Нижний узел обозначен как базисный (для этого используется символ «земля» - точка нулевого потенциала), напряжение верхнего узла относительно базисного обо-
Рис. 3.7 значено как  . Выразим через
. Выразим через
него токи ветвей
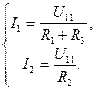 (3.32)
(3.32)
По первому закону Кирхгофа с учетом (3.32) запишем единственное уравнение метода узловых напряжений ( ),
),
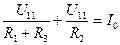 . (3.33)
. (3.33)
Решая уравнение, получим
 , (3.34)
, (3.34)
а из (3.32) определим токи ветвей
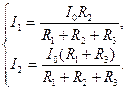 (3.35)
(3.35)
Полученные результаты совпадают с полученными рассмотренными ранее методами.
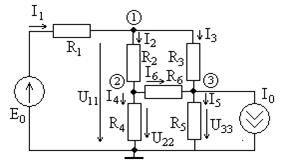 Рассмотрим более сложный пример цепи, показанной на рис. 3.2 при тех же исходных данных, ее схема показана на рис. 3.8. В цепи
Рассмотрим более сложный пример цепи, показанной на рис. 3.2 при тех же исходных данных, ее схема показана на рис. 3.8. В цепи  узла, нижний выбран базисным, а три остальные обозначены номерами в кружках. Введены
узла, нижний выбран базисным, а три остальные обозначены номерами в кружках. Введены
положительные на- Рис. 3.8
правления и обозна-
чения узловых напряжений  ,
, 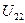 и
и 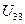 .
.
По Закону Ома с использованием второго закона Кирхгофа определим токи ветвей,

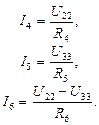 (3.36)
(3.36)
По первому закону Кирхгофа для узлов с номерами 1, 2 и 3 необходимо составить три уравнения,
 (3.37)
(3.37)
Подставляя (3.36) в (3.37), получим систему уравнений метода узловых напряжений,
 (3.38)
(3.38)
После преобразования и приведения подобных получим
 (3.39)
(3.39)
Программа расчета узловых напряжений и токов ветвей приведена на рис. 3.9. Как видно, полученные результаты совпадают с полученными ранее другими методами расчета.
Проведите аналитический расчет узловых напряжений, получите формулы для токов ветвей и вычислите их значения.

Рис. 3.9
3.6. Метод наложения
Метод наложения заключается в следующем.

Расчет проводится следующим образом. В цепи, содержащей несколько источников, поочередно выбирается каждый из них, а остальные отключаются. При этом образуются цепи с одним источником, число которых равно количеству источников в исходной цепи. В каждой из них проводится расчет искомого сигнала, а результирующий сигнал определяется их суммой. В качестве примера рассмотрим расчет тока 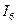 в цепи, показанной на рис. 3.2, ее схема показана на рис. 3.10а.
в цепи, показанной на рис. 3.2, ее схема показана на рис. 3.10а.
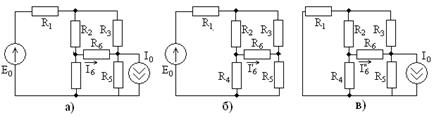
Рис. 3.10
При выключении идеального источника тока (его цепь разрывается) получается цепь, показанная на рис. 3.9б, в которой любым из рассмотренных методов определяется ток 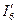 . Затем выключается идеальный источник напряжения (он заменяется коротким замыканием) и получается цепь, показанная
. Затем выключается идеальный источник напряжения (он заменяется коротким замыканием) и получается цепь, показанная
на рис. 3.9а, в которой находится ток  . Искомый ток
. Искомый ток 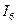 равен
равен
 .
.
Проведите аналитические и численные расчеты самостоятельно, сравните с полученными ранее результатами, например, (3.20).
3.7. Сравнительный анализ методов расчета
Метод расчета, основанный на законе Ома, пригоден для сравнительно простых цепей с одним источником. Его нельзя использовать для анализа цепей сложной структуры, например, мостового типа вида рис.3.9.
Общий метод расчета цепи на основе уравнений законов Ома и Кирхгофа универсален, но требует составления и решения системы из  уравнений, которая легко преобразуется в систему из
уравнений, которая легко преобразуется в систему из  уравнений. При большом числе ветвей резко возрастают вычислительные затраты, особенно при необходимости аналитических расчетов.
уравнений. При большом числе ветвей резко возрастают вычислительные затраты, особенно при необходимости аналитических расчетов.
Методы контурных токов и узловых напряжений более эффективны, так как приводят к системам с меньшим числом уравнений, равным соответственно  и
и  . При условии
. При условии
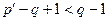 или
или  (3.40)
(3.40)
метод контурных токов эффективнее, а иначе целесообразно применять метод узловых напряжений.
Метод наложения удобен, когда при отключении источников происходит резкое упрощение цепи.
В системах схемотехнического моделирования цепей, например, MicroCAP или OrCAD в основном применяют метод узловых напряжений.
3.8. Задания для самостоятельного решения
Задание 3.1 С помощью закона Ома определите напряжение 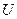 в цепях, схемы которых показаны на рис. 3.11 при
в цепях, схемы которых показаны на рис. 3.11 при 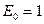 В,
В,  мА,
мА, 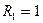 кОм,
кОм, 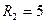 кОм,
кОм, 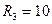 кОм.
кОм.
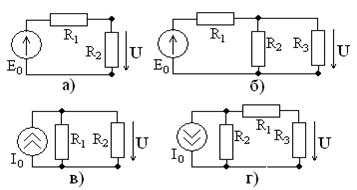
Рис. 3.11
Задание 3.2 Общим методом расчета на основе законов Ома и Кирхгофа определите ток 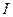 в цепях, схемы которых показаны на рис. 3.11 при
в цепях, схемы которых показаны на рис. 3.11 при 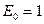 В,
В, 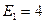 В,
В,  мА,
мА, 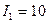 мА,
мА, 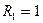 кОм,
кОм, 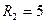 кОм,
кОм, 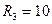 кОм.
кОм.
Задание 3.3 Методами контурных токов, узловых напряжений и наложения определите ток 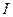 в цепях, схемы которых показаны на рис. 3.12, параметры цепи возьмите из задания 3.1, сравните полученные результаты.
в цепях, схемы которых показаны на рис. 3.12, параметры цепи возьмите из задания 3.1, сравните полученные результаты.
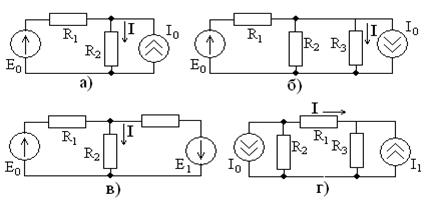
Рис. 3.12
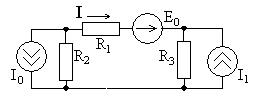 Задание 3.4. Методами контурных токов и узловых напряжений определите ток
Задание 3.4. Методами контурных токов и узловых напряжений определите ток 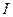 в цепи, схема которой показана на рис. 3.13 при
в цепи, схема которой показана на рис. 3.13 при 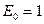 В,
В,  мА,
мА, 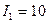 мА,
мА, 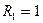 кОм,
кОм, 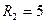 кОм,
кОм,
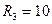 кОм. Рис. 3.13
кОм. Рис. 3.13
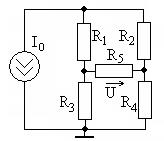
Задание 3.5. Общим методом расчета, методами контурных токов и узловых напряжений определите в цепи рис. 3.14 напряжение 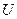 при
при 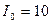 мА
мА 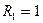 кОм,
кОм,  кОм,
кОм,  кОм,
кОм,  кОм,
кОм, 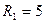 кОм. Проведите сравнительный анализ
кОм. Проведите сравнительный анализ
методов расчета. Рис. 3.14
4. ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ
Дата добавления: 2015-07-25; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЭЛЕКТРИЧЕСКИЕ СИГНАЛЫ | | | В ЛИНЕЙНЫХ ЦЕПЯХ |