Элементы алгебры логики.

Поскольку в цифровых устройствах используются только два символа 0 и 1, алгебра логики использует логические переменные и функции от них, которые также принимают только два значения - 0 и 1. В логике символы 0 и 1 не цифры. Единица обозначает абсолютную истину, символ 0 - абсолютную ложь. Основы алгебры логики придумал в середине XIX века ирландский математик Дж. Буль, поэтому алгебра логики иногда называется булева алгебра.

В отличие от обычной математики, в алгебре логики операции сложения и умножения заменяют операцией логического умножения (конъюнкция), и операцией логического сложения (дизъюнкция). Для обозначения операций сложения и умножения используют специальные символы: \/ - логическое сложение, /\ - логическое умножение, но мы для простоты будет обозначать привычными нам + и х, все равно правильно.

Операция логического сложения обозначается союзом "ИЛИ".

Логическое умножение обозначается союзом "И". В двух словах: для логического сложения результат равен нулю только при совпадении нулей, для логического умножения результат равен единице только при совпадении единиц.

Есть еще понятие отрицания, обозначаемое "НЕ". Обозначается отрицание чертой над обозначением переменной или символом, стоящим перед переменной. Например, ā означает отрицание a.

Понятие двоичной переменной, логических операций И, ИЛИ, НЕ образуют систему аксиом алгебры логики.

Аналогично обычной алгебре, в булевой действительны свойства перестановки, сочетательности и распределительности:a + b = b + a

a x b = b x a

a + (b + c) = (a + b) + c

a x (b x c) = (a x b) x c

a x (b + c) = a x b + a x c

Помимо этих есть и другие, свойственные только алгебре логики, законы:

Законы одинарных элементов

a x 1 = a

a + 1 = 1

a x 0 = 0

a + 0 = a

Законы отрицания

(правила де Моргана)

Распределительность дизъюнкции:

a + (b x c) = (a x b) + (a x c)

Правила поглощения

a + (a x b) = a

a x (a + b) = a

Эти правила и законы позволяют значительно упростить логические уравнения и функции.

Рассмотрим логические элементы, реализующие все вышеперечисленное.

Схема "И"

Двухвходовый логический элемент "И" обозначается вот так:

x2	x1	y

- таблица истинности логического элемента. Таблицы истинности присуще всем цифровым устройствам. В этой таблице символы x1 и x2 означают входные сигналы, y - выходные. Причем входы принято обозначать слева (это касается любых устройств), выходы - справа. Переменная х с индексом 1 обозначает младший разряд, x2 - старший. Судя по таблице, единица будет на выходе только тогда, когда на обоих входах будут единицы. Символ & говорит о том, что это элемент "И".

Схема "ИЛИ"

Логический элемент "ИЛИ" обозначается так:

Его таблица истинности:

x2	x1	y

То есть, единица на выходе тогда, когда хотя бы на одном из входов присутствует единица. Символ 1 говорит о том, что это элемент "ИЛИ".

Схема "НЕ"

Логический элемент "НЕ", который иначе называется инвертор, обозначается так:

Таблица истинности:

x	y

Базисные элементы

Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. Простым языком, базис - это те элементы, при помощи которых можно сделать любое устройство (речь идет о цифровой технике).

Базис "И-НЕ"

И-НЕ - это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент называется инверсией логического умножения или отрицанием логического умножения, ну или инверсией конъюнкции и еще красивым словосочетанием штрих Шеффера. Штрих кого-то там называется потому, что в виде формулы операция И-НЕ записывается так: y = x1 | x2. Вертикальная черта между иксами и есть штрих какого-то Шеффера.

Логический элемент И-НЕ обозначается так:

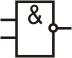
Таблица истинности для него:

x2	x1	y

Базис ИЛИ-НЕ

Здесь все по аналогии с элементом И-НЕ. Операция, выполняемая элементом ИЛИ-НЕ, называется инверсией логического сложения или инверсией дизъюнкции или стрелка Пирса. Стрелка потому, что в виде формулы функция записывается так: y = x 1↓ x2.

Обозначается элемент ИЛИ-НЕ так:

Таблица истинности:

x2	x1	y

Рассмотрим элемент "ИСКЛЮЧАЮЩЕЕ-ИЛИ".

Операция, выполняемая таким элементом называется сложение по модулю два и обозначается плюсиком в кружочке, т. е. вот таким символом ⊕. В виде уравнения функция записывается так: X1⊕X2. Читается это, как "либо икс один, либо икс два". Обозначение элемента ИСКЛЮЧАЮЩЕЕ-ИЛИ следующее:

Таблица истинности:

x2	x1	y

Этот элемент можно заменить логическими элементами И, ИЛИ, НЕ, поскольку:

Для наглядности составим схему из базисных элементов (И-НЕ, ИЛИ-НЕ):

23. Комбинационные логические схемы и их синтез.

Основные теоремы

Как и другие разделы математики, булева алгебра основывается на ряде постулатов, в частности на тех, которые были выдвинуты Хантингтоном в 1904 г. Их следствием являются следующие соотношения для логических переменных, принимающих значения О и 1:

	(2.8а)		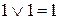(2.8б)
	(2.9а)		(2.9б)
	(2.10а)		(2.10б)
	(2.11а)		(2.11б)

Равенства (2.8а)—(2.10а) соответствуют операции И для двух переменных согласно таблице истинности 2.1; равенства (2.8б)— (2.10б) соответствуют операции ИЛИ (табл. 2.2), а равенства (2.11)—операции НЕ (табл. 2.3). При сравнении выражений (2.8а)—(2.11а) и (2.86)—(2.116) можно заметить, что булевы функции обладают свойством двойственности. Действительно, если в приведенных равенствах заменить 0 на 1, 1 на 0, а затем зна­ки Ù на Ú, то выражения (2.8а)–(2.11а) трансформируются в выражения (2.86)—(2.116). Для большей наглядности соответ­ствующие равенства расположены попарно.

Приведенные равенства справедливы также для булевых пере­менных А, В и С. Важные свойства этих логических переменных иллюстрируются следующими попарно объединенными равенст­вами:

	(2.12а)		(2.12б)
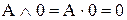
	(2.13а)		(2.13б)
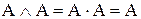
	(2.14а)		(2.14б)
	(2.15а)		(2.15б)
Выражения (2.12)-(2.15) – закон идемпотентности.
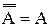
	(2.16)	закон двойного отрицания
	(2.17а)		(2.17б)
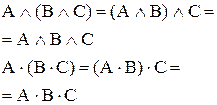
	(2.18а)		(2.18б)
	(2.19а)		(2.19б)
	(2.20а)		(2.20б)

Равенства (2.12) — (2.16) характеризуют свойства операций И, ИЛИ и дополнения для логической переменной А, а равенства (2.17)—(2.20) выражают соответственно переместительный (коммутативности), соче­тательный (ассоциативности), распределительный (дистрибутивности) законы и закон поглощения. Любое из равенств (2.12)—(2.20) можно реализовать при помощи схем И, ИЛИ, НЕ, описанных в предыдущем разделе. Рассмотрим в качестве примера двойное дополнение (2.16); это равенство можно реализовать при помощи двух инверторов (рис. 2.9.).

Рис. 2.9. Логическая схема двойного дополнения.

На рис. 2.10 приведены две схемы для выражения (2.19б), характеризующего распределительный закон. Эти схемы эквивалентны, но одна из них состоит из двух, а другая – из трех элементов.

Рис. 2.10. Логические схемы реализации выражения

Важные соотношения булевой алгебры можно получить, используя теорему де Моргана. Согласно этой теореме, выражения, характеризующие свойства конъюнкции и дизъюнкции переменных А, В и С, связаны между собой следующим образом:

(2.21а)

(2.21б)

Теорема де Моргана полезна при выполнении двойственных преобразований булевых выражений. Преобразование согласно этой теореме заключается во взаимной замене знаков Ú и Ù и замене всех переменных их дополнениями. Рассмотрим, например, трехвходовую схему И. Из (2.16) и (2.21а) получаем

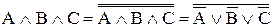(2.22)

Схема реализации этого выражения показана на рис. 2.11.

Рассмотрим пример упрощения выражения.

Пример 2.1. Выражение

можно упростить следующим образом:

		по теореме (2.19б)
		по теореме (2.15а)
		по теореме (2.12б)

Пример 2.2. Выражение

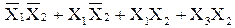
		по теореме (2.14б)
		по теореме (2.19а)
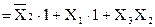
		по теореме (2.15б)
		по теореме (2.12а)
		по теореме (2.20б)

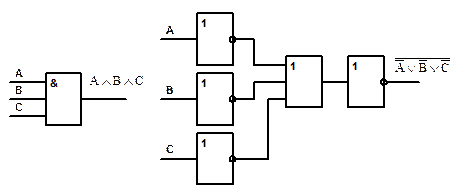
Рис. 2.11. Логическая схема реализации выражения

Выходные сигналы комбинационных логических схем опреде­ляются только значениями входных сигналов в любой данный мо­мент времени. Благодаря этой особенности разработка комбина­ционной схемы относительно проста. Первым шагом в процессе разработки является составление таблицы истинности, в которой для всех комбинаций входных сигналов указываются соответст­вующие выходные сигналы. С целью пояснения сказанного рас­смотрим, как реализуется логическая схема, выполняющая опера­цию ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2), или операцию несовпадения. Эта схема особенно часто используется в арифметических сумматорах. Таблица истинности 2.6 описывает работу данной схемы. Сигнал на выходе принимает истинное значение только в том слу­чае, когда значения входных сигналов не совпадают.

Таблица 2.6.

Таблица истинности для схемы ИСКЛЮЧАЮЩЕЕ ИЛИ
А	В	X

В таблице истинности 1 соответствует переменной А (ИСТИ­НА), 0 – (ЛОЖЬ). Из таблицы видно, что значение Х на выхо­де истинно при следующих комбинациях входов А и В: и В или А и .

Это можно записать следующим образом:

(2.23)

Выражение (2.23) известно как выражение для получения суммы произведений; последние называют минитермами. На рис. 2.12 изображена схема реализации операции ИСКЛЮЧАЮ­ЩЕЕ ИЛИ (2.23). В этой схеме используются элементы И, ИЛИ и НЕ. Поскольку любую функцию можно реализовать с использо­ванием указанных элементов, такую комбинацию элементов назы­вают функционально полной. Существуют другие функционально полные системы, например система, реализующая функцию И-НЕ, или система, реализующая функцию ИЛИ-НЕ.

Рис. 2.12. Логическая схема ИСКЛЮЧАЮЩЕЕ ИЛИ.

Операция ИСКЛЮЧАЮЩЕЕ ИЛИ обычно записывается как 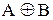и читается «А исключающее или В». Соответствующие ус­ловные обозначения схемы представлены на рис. 2.13. Комбина­ционные схемы часто используются при преобразовании кодов.

Рис. 2.13. Условное обозначение Схемы ИСКЛЮЧАЮЩЕЕ ИЛИ.

Дата добавления: 2015-07-25