Возмущения химических связей.

Пусть за счет внешнего возмущения, направленного на химическую связь между атомами r и s, соответствующий резонансный интеграл b _rs изменился на небольшую величину db _rs:

b _rs ® b _rs + db _rs

Тогда это возмущение, аналогично возмущению атома, вызовет изменения во всех атомных электронных плотностях и порядках связей:

` n<sub>t</sub> ® ` n_t + d n_t

P_tu ® P_tu + d P_tu

Изменения d n_t и d P_tu в первом приближении будут пропорциональны степени возмущения db _rs (т.е. следствие пропорционально причине):

d n_t = p _{t, rs} • db _rs

d P_tu = p _{tu, sr} • db _rs

Коэффициенты пропорциональности называются поляризуемостями "атом-связь" (p _{t, sr}) и "связь-связь" (p _{tu, rs}). Поляризуемость p _{t, sr} показывает, насколько электронная плотность на атоме t чувствительна к возмущениям резонансного интеграла связи между атомами r и s. Поляризуемость p _{tu, sr} показывает, насколько электронная плотность между атомами t и u (т.е. порядок связи P_tu) чувствительна к возмущениям резонансного интеграла связи между атомами r и s.

Поляризуемости p _{r, r} и p _{rs, rs} часто называют атомными и связевыми самополяризуемостями.

Для поляризуемостей выполняется ряд полезных соотношений.

1) p _rs = p _sr = ¶ n_s / ¶a _r = ¶ n_r / ¶a _s

2) p _{st, r} = ¶ P_st / ¶a _r

3) p _{t, rs} = ¶ n_t / ¶b _rs = 2p _{st, r} = 2 ¶ P_st / ¶a _r

4) p _{tu, rs} = p _{rs, tu} = ¶ P_tu / ¶b _rs = ¶ P_rs / ¶b _tu

5) p _{r, r} < 0; p _{rs, rs} < 0

6) å p _rs = 0; å p _{t, rs} = 0

Зная величины поляризуемостей, можно сравнительно легко и надежно решать ряд химических задач:

1) предсказывать результат внешнего возмущения в виде изменений в зарядах атомов и порядках связей, а, следовательно, и в реакционной способности молекулы:

2) анализировать закономерности в изменения свойств в рядах аналогичных по строению молекул.

Например, в молекуле нафталина все атомы скелета одинаковы (атомы углерода) и поэтому электронная плотность распределена равномерно — заряды всех атомов равны нулю. Замещение одного из атомов углерода на атом азота с более отрицательным значением остовного интеграла (a_N) вызовет перераспределение электронной плотности. На некоторых атомах, для которых поляризуемость отрицательна, электронная плотность возрастет (da < 0) и появятся отрицательные заряды. На других атомах, для которых поляризуемость положительна, электронная плотность снизится (da > 0) и появятся положительные заряды.

Рассмотренные численные характеристики молекулы, имеющие локальный характер: атомные электронные плотности и заряды атомов, порядки связей, индексов свободной валентности, поляризуемости и др. часто используются для оценки реакционной способности молекулы и в этом случае называются индексами реакционной способности (ИРС).

Так же как метод ВС, метод МО имеет множество приближенных вариантов, основным из которых является метод локализованных МО (ЛМО).

Метод ЛМО (локализованные молекулярные орбитали)

Рассмотренный выше вариант метода МО ЛКАО — метод канонических молекулярных орбиталей (КМО), отличается тем, что он плохо согласуется с классическими структурными представлениями о молекуле, как совокупности атомов, связанных локализованными и бинарными химическими связями. Строго говоря, в методе КМО отсутствуют даже сами понятия "атом" и "химическая связь". Поэтому были разработаны и другие варианты метода МО, более адаптированные к классическим структурным моделям молекулы. Одним из них является метод локализованных молекулярных орбиталей (ЛМО).

В основе метода лежит предположение о том, что любую молекулу можно построить из двух фрагментов: X_nA* + *BY_m ¾® X_nA—BY_m

Предполагается также, что реакционная способность фрагментов локализована на их отдельных атомах A* и *B, так что в результате их химического взаимодействия образуется бинарная и локализованная связь A—B. При этом остальные фрагменты молекулы (атомы X и Y) сами не изменяются и не влияют на взаимодействие химически ненасыщенных атомов А и В.

В результате такого представления оказывается возможным описать в рамках метода МО только фрагмент молекулы, включающий два выделенных атома и химическую связь между ними, абстрагируясь от остальных ее частей. Затем процедура описания поочередно повторяется для всех остальных связей:

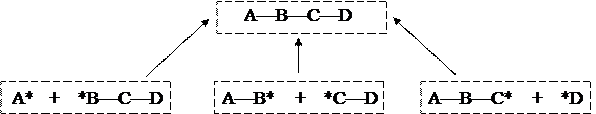Другими словами, вместо одной глобальной модели молекулы получается множество локальных моделей — по одной для каждой химической связи (пары связанных атомов). Эти модели удобны еще и тем, что они являются двухэлектронными, как в простейшем случае молекулы водорода (см. задачу о молекуле водорода в семинарских занятиях):

–А• •В– ÜÞ –А—В– ÜÞ (–А: ^– É⁺В–)

В результате построение таких локальных моделей гораздо проще, чем глобальной КМО-модели. Из теории двухатомных молекул известно, что при взаимодействии двух атомов (А и В), поставляющих по одному электрону, каждый из которых находится на своей атомной орбитали (а и b, соответственно), волновая функция молекулы получается в виде определителя Слэтера:

Ф = || j₁ j₂ ||

где молекулярные орбитали (j₁ и j₂) имеют универсальную форму:

j₁ = C ₁₁ • a + C ₁₂ • b j₂ = C ₂₁ • a – C ₂₂ • b

причем для разных типов взаимодействующих атомов отличия сводятся лишь к конкретным числовым значениям коэффициентов С_ij. Другими словами, всегда образуется одна безузловая МО и одна МО с единственным узлом между ядрами взаимодействующих атомов.

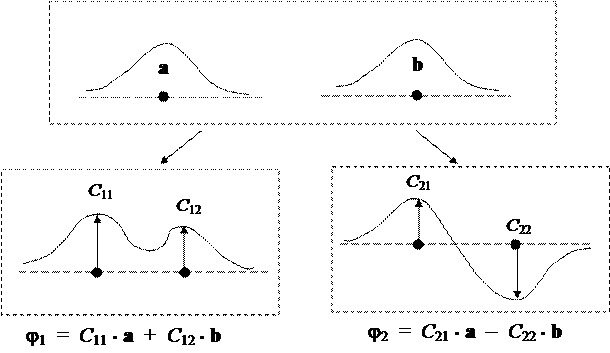Энергетические и корреляционные диаграммы разных двухатомных молекул также выглядят в качественном отношении одинаково.

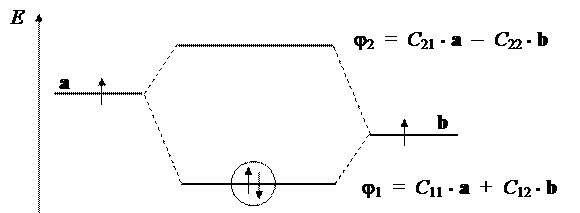Можно заметить, что одна из МО (безузловая) всегда имеет энергию ниже, чем у любой из базисных АО, тогда как энергия второй МО всегда выше. Поэтому переход электрона с АО на безузловую МО (j₁) сопровождается уменьшением энергии и возрастанием устойчивости молекулы. Напротив, переход электрона с АО на МО с узлом (j₂) сопровождается возрастанием энергии и снижением устойчивости молекулы. По этой причине первая МО обычно называется связывающей, а вторая — разрыхляющей.

Ввиду локального характера ЛМО, их симметрия также описывается локальным образом — относительно ТГС не всей молекулы, а лишь ее двухатомного фрагмента. Такие фрагменты всегда имеют одну и ту же аксиальную симметрию. ЛМО, соответствующие типам симметрии в этом случае имеют в поперечном разрезе следующий вид:

Здесь легко увидеть аналогию с шаровыми АО s -, p -, d -типов, из которых данные ЛМО и образуются. Отсюда следует важный вывод: при образовании химической связи состояния электронов взаимодействующих атомов должны относиться к одному типу симметрии. В противном случае интеграл перекрывания будет равен нулю и взаимодействие атомов не приведет к образованию химической связи. В этом отношении часто говорят об "эффективных" и "не эффективных" способах перекрывания АО.

Таким образом, модель электронной оболочки молекулы в методе ЛМО выглядит следующим образом.

1) Каждой паре химически связанных атомов (т.е. химической связи, валентному штриху, льюисовской связывающей электронной паре) сопоставляется орбитальная модель, включающая две ЛМО:

а) связывающую (не имеющую узлов), с пониженной энергией, заселенную электронной парой,

б) разрыхляющую (с одним узлом), с повышенной энергией, не заселенную электронами (вакантную).

2) В случае кратных связей между двумя атомами, каждая связь считается независящей от остальных и описывается отдельно.

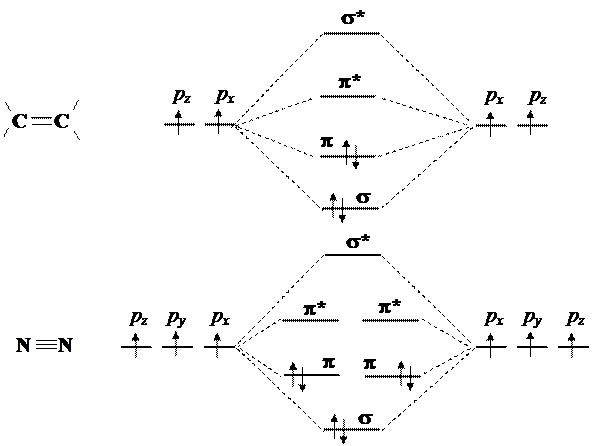3) У некоторых атомов остаются электроны, не участвующие в образовании связывающих пар — несвязывающие или неподеленные электроны или электронные пары. Такие электроны описываются локализованными АО, не участвующими в линейных комбинациях с другими АО. Некоторым атомам приписываются вакантные АО, также не участвующие в линейных комбинациях с другими АО. Такие АО называются лакунами.

Примерами таких молекул могут служить соединения трехвалентного азота и трехвалентного бора:

Главное достоинство метода ЛМО заключается в его почти полном соответствии классическим структурным представлениям, когда молекула рассматривается как совокупность атомов, связанных химическими связями. Классический подход к строению молекулы сохраняется и в электронной теории Льюиса, где в структурной модели молекулы валентные штрихи заменяются связывающими электронными парами, и, кроме того, добавляются неподеленные электронные пары и лакуны. В методе ЛМО связывающим электронным парам сопоставляется связывающая ЛМО, а неподеленным парам и лакунам — атомные орбитали.

Другими словами, модель ЛМО можно рассматривать как развитие и усовершенствование классической теории химического строения молекул.

В результате введения модели ЛМО химики получают возможность решать ряд важных задач:

1) обсуждать и объяснять химические свойства молекул, установленные экспериментально,

2) интерпретировать классические структурные характеристики молекулы с учетом движения электронов и квантовомеханических законов,

3) ввести и использовать новые характеристики химических связей, такие как:

а) симметрия и узловая структура электронного облака;

б) тип связи: s-, p-, d- связи, s - s, s - p, p - p -связи и т.д.;

в) частичные электрические заряды атомов;

г) порядки связи;

д) индексы свободной валентности;

е) поляризуемости различных типов и др.

4) интерпретировать квантовомеханические понятия и численные параметры орбитальной модели на основе экспериментальных химических данных.

Модель ЛМО имеет ряд существенных недостатков. Во-первых, эта модель явным образом противоречит квантовой механике: всякий электрон в составе молекулы должен двигаться во всем ее объеме и не может быть локализован в окрестности только двух ядер. Второй, наиболее важный, момент заключается в том, что во многих случаях простая модель ЛМО приводит к противоречию с опытом, что требует введения многочисленных поправок и дополнений в структурную модель молекулы, получаемую в рамках метода ЛМО. Рассмотрим два типа таких поправок.

Гибридизация АО

Возьмем для примера комплексный ион аммиаката никеля: [Ni(NH₃)₆]²⁺. Классическая структурная модель предсказывает наличие в этом ионе шести одинаковых связей (Ni—NH₃) между ионом-комплексообразователем и лигандами. Поскольку в рамках метода ЛМО каждой связи соответствует пара перекрывающихся АО, ион никеля должен располагать шестью вакантными АО, необходимых для принятия электронных пар от лигандов, причем все они должны быть абсолютно одинаковы:

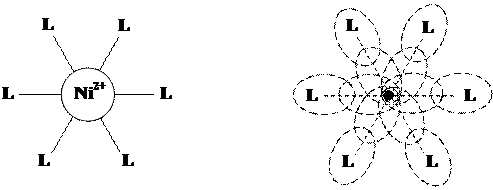В то же время, орбитальная модель иона никеля приводит к другой картине:

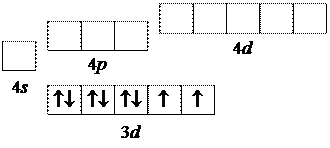Следовательно, мы должны либо отказаться от применения метода ЛМО, либо предположить, что в процессе образования комплекса некоторые орбитали иона никеля претерпевают определенное изменение:

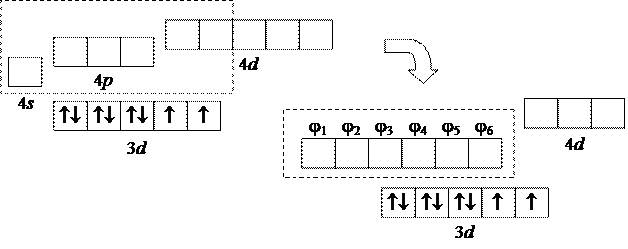В результате такой "перегруппировки" из разных АО образуются одинаковые:

4 s + 4 p_x + 4 p_y + 4 p_z + 4 d' + 4 d'' = 6 j

Такой процесс называется гибридизацией, а образующиеся АО — гибридизованными или гибридными орбиталями (ГАО). Возможность такого процесса вполне очевидна с точки зрения основного закона квантовой механики — принципа суперпозиции. Шаровые АО образуют всего лишь один их базисных наборов в пространстве состояний атома. Именно этот набор является стационарным в условиях полной изоляции атома, когда атом сферически симметричен. Однако, когда атом взаимодействует с окружением из шести лигандов, расположенных по вершинам октаэдра, стационарным становится другой набор, а именно — набор гибридизованных АО. Отсюда вытекает и способ построения ГАО из исходных шаровых АО. Два любых базиса связаны линейным преобразованием посредством некоторого унитарного оператора:

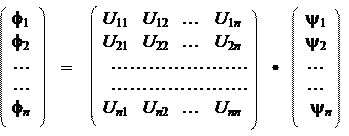Другими словами, каждая ГАО является линейной комбинацией шаровых АО, задаваемой коэффициентами матрицы U. Конкретный тип гибридизации определяется симметрией окружения атома. Так, для иона никеля в октаэдрическом окружении шести лигандов стационарными являются ГАО sp ³ d ³-типа, для атома углерода в тетраэдрическом окружении (метан, четыреххлористый углерод и др.) стационарным является базисный набор ГАО sp ³-типа и т.д.

Несмотря на большое разнообразие геометрических форм молекул, обычно используется небольшой набор типов гибридизации, который соответствуют геометрически правильным многогранникам:

Тип молекулы	Тип гибридизации АО центрального атома
Линейный L1—A— L2	sp
Плоский треугольный АL3	sp^2
Тетраэдрический AL4	sp^3
Плоский квадратный ML4	dsp^2
Тригональная бипирамида ML5	sp^3d или dsp^3
Тетрагональная бипирамида (октаэдр) ML6	sp^3d^2 или d^2sp^3

Можно отметить, что ГАО отличаются от шаровых АО в отношении пространственной формы. Если шаровые АО центрированы на ядре и принадлежат определенному типу симметрии (т.е. при действии операций симметрии переходят сами в себя с сохранением знаков или с переменой их на противоположные), то ГАО уже не являются центрально-симметричными. Хотя узловая структура сохраняется, части ГАО, разделенные узловой поверхностью, не равны друг другу. Следствием этого является наличие выделенной пространственной ориентации ГАО в пространстве. Для примера рассмотрим простой случай гибридизации: ГАО₁ = s + p_x

Из рисунка видно, что полученная ГАО вытянута в положительном направлении оси Х и имеет не шаровую, а только аксиальную симметрию. Аналогичный вид имеет и вторая ГАО (s – p_x), но она вытянута в противоположном направлении.

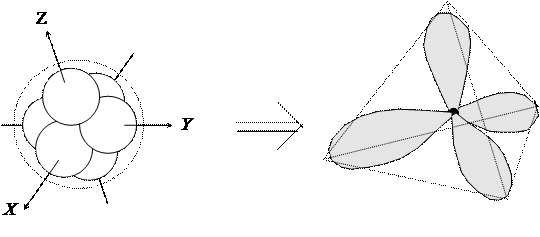
В случае молекулы метана исходный шаровой базис надо преобразовать так, чтобы в результате получить набор 4-х ГАО, отличающихся друг от друга только ориентацией в пространстве около ядра атома С. Для решения этой задачи подходит следующее преобразование:

ГАО данного вида называются sp³-гибридизованными (каждая является ЛК s‑ орбитали и трех р -орбиталей). Если построить полярные диаграммы этих ГАО, то будет ясно видна их идентичность друг другу. Единственное отличие между ними заключается в том, что они ориентированы по различным направлениям в пространстве — по вершинам тетраэдра.

Другой случай гибридизации имеет место для атомов углерода, имеющих только три соседних (химически связанных) атома, как это имеет место в случае молекул этилена или бензола. Такие атомы имеют плоскую конфигурацию и для образования трех однотипных связей со своими соседями атом углерода должен иметь три идентичные ГАО, направленные по вершинам плоского треугольника. Такие ГАО можно получить, строя ЛК из трех шаровых АО: (2 s 2 p_x 2 p_y) ¾® (ГАО₁ ГАО₂ ГАО₃ ). Они имеют следующий вид:

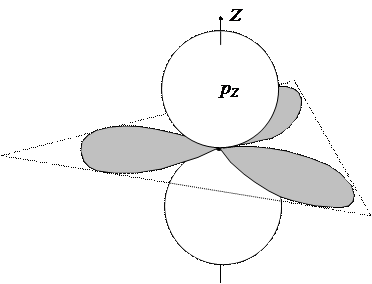ГАО такого типа называются sp ²-гибридизованными. Характерно, что, наряду с тремя ГАО, атом углерода сохранил и одну негибридизованную (шаровую) АО, которая может участвовать в образовании ЛМО p-типа.

Таким образом, ГАО вытянуты вдоль определенных пространственных осей, соответствующих расположению химических связей в молекуле. Поэтому геометрия совокупности ГАО всегда полностью соответствует геометрии молекулы. Это позволяет, с одной стороны, подбирать тип гибридизации на основе информации о геометрии молекулы, а с другой стороны, по типу гибридизации предсказывать эту геометрию. Следует подчеркнуть, что концепция гибридизации АО необходима только в рамках приближенной модели ЛМО.

Эффекты сопряжения

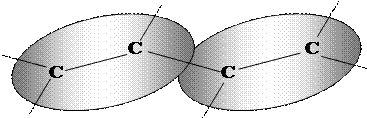
В модели ЛМО предполагается, что электроны образуют локализованные двухцентровые облака, которым и соответствуют ЛМО. Достаточно очевидно, что такое представление физически неверно — каждый электрон молекулы может двигаться во всем ее объеме. Для того, чтобы в некоторой степени исправить этот недостаток модели ЛМО, ее дополняют т.н. "эффектами сопряжения", смысл которых сводится к учету перекрывания соседних двухцентровых электронных облаков. Например, в молекуле бутадиена (С=С—С=С) предполагается наличие двух пар p-ЛМО:

Электронные облака предполагаются достаточно объемными, так что они способны перекрываться в пространстве. Это перекрывание должно приводить к взаимодействию электронных пар и изменениям в характере их движения. На энергетической диаграмме это выражается следующим образом:

В результате взаимодействия электронные облака делокализуются и соответствующие им делокализованные орбитали (ДЛМО) становятся похожими на КМО.

Характер перераспределения электронной плотности в молекуле за счет эффекта сопряжения отражается в классических структурных формулах с помощью изогнутых стрелок или т.н. "неклассических формул":

На этом примере можно видеть, что введение эффектов сопряжения сближает метод ЛМО с методом резонанса. Неклассическая формула, получаемая посредством учета эффекта сопряжения, может быть получена как резонансный гибрид двух РФ:

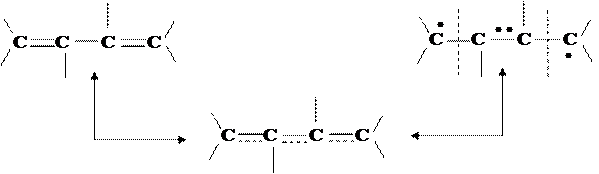Поэтому, по аналогии с методом резонанса, эффекты сопряжения в методе ЛМО часто называют "мезомерными эффектами".

Эффекты сопряжения проявляются не во всех случаях одинаково. Можно выделить несколько типичных ситуаций, когда этими эффектами нельзя пренебрегать.

1) p–p-сопряжение, имеющее место при определенном (соседнем) расположении в молекуле кратных связей p-типа (аналогично тому, как это имеет место в молекуле бутадиена):

.

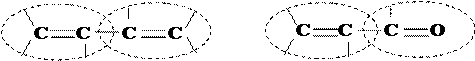2) n –p-сопряжение, когда вместо одной из кратных связей имеется неподеленная пара электронов, заселяющая атомную орбиталь:

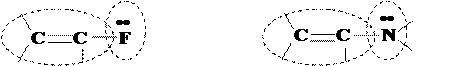3) р –p-сопряжение, когда вместо одной из кратных связей имеется вакантная АО, локализованная на электронодефицитном атоме:

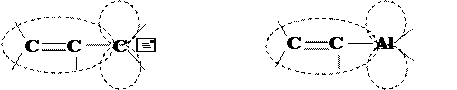4) s–p-сопряжение или гиперконъюгация (сверхсопряжение), когда вместо одной из кратных связей имеется достаточно полярная s-связь (обычно, с атомом водорода):

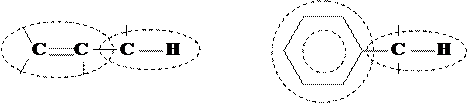Результатом учета эффектов сопряжения (мезомерных эффектов) является некоторая делокализация электронов молекулы, и, следовательно, приближение грубой модели ЛМО к более правильной — модели КМО.

Индуктивные эффекты.

Двухцентровые орбитали, используемые в модели ЛМО, также позволяют рассчитывать атомно-связевые характеристики, такие как средние электронные плотности на атомах, порядки связей, поляризуемости и т.д. Все эти характеристики, однако, относятся лишь к тому двухядерному фрагменту молекулы, но который распространяются ЛМО. В частности, избыточные электрические заряды, рассчитываемые через коэффициенты ЛМО, всегда характеризуют только два химически связанных атома.

Например, в молекуле алкилгалогенида связь C—Cl можно описать парой электронов, заселяющей ЛМО s-типа:

s = D ₁ • sp ³(C) + D ₂ • p (Cl)

При этом, в соответствии с общим правилом, средние электронные плотности атомов углерода и хлора будут равны 2(D ₁)² и 2(D ₂)², соответственно. Поскольку коэффициенты неодинаковы (D ₁ < D ₂), то на атоме хлора будет избыточный отрицательный заряд, а на атоме углерода — положительный.

В действительности, распределение электронной плотности более равномерное, что отражается поправкой, вносимой в модель ЛМО, называемой индуктивным эффектом. Смысл этого эффекта сводится к индуктивному поляризующему влиянию дипольного момента связи C—Cl на соседние фрагменты молекулы:

Другими словами, индуктивный эффект показывает, что влияние электроноакцепторного или электронодонорного атома не ограничивается только его непосредственными соседями, но и распространяется на атомы второго окружения и т.д., а в конечном итоге — на всю молекулу. Индуктивное влияние значительно ослабевает по мере увеличения числа участвующих в нем химических связей.

Таким образом, мезомерные и индуктивные эффекты позволяют до некоторой степени исправить грубую картину распределения электронной плотности в молекуле, даваемую методом ЛМО. Соответственно, такие исправления вносятся и в заряды атомов, и в порядки связей.

Следует подчеркнуть, что поправки в виде мезомерных и индуктивных эффектов носят, как правило, качественный характер. К сожалению, простых и надежных способов количественного учета таких эффектов не существует. Поэтому при необходимости получать количественные результаты следует пользоваться методом КМО, невзирая на отсутствие у него наглядности и согласованности с классическими структурными представлениями.

Таким образом, строение электронной оболочки молекулы можно описывать по-разному:

1) посредством полных методов ВС или КМО, позволяющих построить глобальную электронную волновую функцию в виде комбинации АО тех атомов, которые участвуют в построении молекулы;

2) посредством различных приближенных и упрощенных вариантов, таких как метод резонанса, метод ЛМО и др., которые более или менее адаптированы к классическим химическим представлениям.

Выбор варианта описания определяется характером поставленных химических задач. Профессиональная грамотность и искусство химика определяются его умением выбрать такой способ описания, который приводил бы к надежным и полезным результатам с наименьшими усилиями.

Дата добавления: 2015-07-20