Проблема оптимизации коэффициентов

Основная проблема метода ВС заключается в оптимизации волновой функции, т.е. в установлении значений коэффициентов (С ₁, С ₂,..., C_N). Известно несколько общих правил, облегчающих выполнение этой задачи.

1) Волновая функция молекулы должна удовлетворять требованиям симметрии. Для молекул эти требования более разнообразны, чем для атомов.

а) Должен выполняться принцип Паули — волновая функция должна быть антисимметричной, относительно перестановки местами двух любых электронов: Ф (1, 2, …, i, j, …, n) = – Ф (1, 2, …, j, i, …, n).

В частности, все слагаемые, входящие в волновую функцию должны быть либо антисимметричными, либо образовывать с другими слагаемыми антисимметричные комбинации.

б) У любой молекулы имеется пространственная симметрия, выражаемая одной из точечных групп симметрии (ТГС). Волновая функция молекулы должна принадлежать одному из типов симметрии (неприводимых представлений) этой ТГС или, другими словами, быть собственной функцией операторов симметрии, входящих в ТГС.

Ф Î НП ТГС или FФ = c Ф = (±1) Ф

Так, если имеется несколько РФ, переводимых друг в друга операциями пространственной симметрии, то коэффициенты при их волновых функциях должны быть одинаковы по модулю (т.е. могут отличаться только знаками).

2) Абсолютная величина коэффициентов при базисных волновых функциях конкретных РФ сильно зависит от их энергий: чем выше энергия РФ, тем меньший вклад в молекулярную волновую функцию она вносит. Например, энергии РФ, составленных их "ионов", существенно выше энергии РФ, составленных из нейтральных "атомов". Это обстоятельство, в большинстве случаев, позволяет не рассматривать полный набор РФ, а ограничиться небольшим их числом, т.е. включать в линейную комбинацию только те РФ, энергии которых заметно ниже остальных.

3) Волновая функция должна быть нормированной.

После учета всех этих правил, коэффициенты линейной комбинации оптимизируются на основе вариационного принципа: составляется выражение для полной энергии молекулы, включающее неизвестные коэффициенты, и этот функционал минимизируется.

E = f (С ₁, С ₂,..., C_N) Þ min

Для явного выражения энергии молекулы как функции коэффициентов С_i используется стандартное уравнение: E = òФ Н Ф dv.

Оператор Гамильтона для молекулы можно легко построить в любом случае. Если считать ядра неподвижными и пренебречь магнитными взаимодействиями (нерелятивистская модель), то он будет иметь вид:

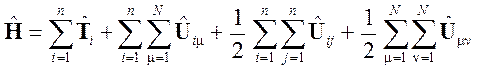
где T _i = (–h²/2 m)Ѳ _i — оператор кинетической энергии i -го электрона,

U _{i m} = – Z _m e ²/ r_{i m} — оператор потенциальной энергии i -го электрона в кулоновском поле m-го ядра,

U _ij = e ²/ r_ij — оператор кулоновского отталкивания для пары электронов (с номерами i и j),

U _mn = Z _m Z _n e ²/ r _mn — оператор кулоновского отталкивания для пары ядер (с номерами m и n).

Эта форма гамильтониана приводит к тому, что выражение для полной энергии молекулы приобретает вид:

где Е _m — полная энергия изолированного атома с номером m,

J _mn — межатомные кулоновские интегралы (энергии кулоновского отталкивания атомов),

K _mn — межатомные обменные интегралы (поправки к энергии за счет перехода электронов от одного атома к другому.

Можно заметить, что сами одноатомные энергии (Е _m) могут быть выражены сходными формулами (см. теорию МЭА):

Е _m = å H_i + åå(J_ij ± K_ij) (i < j)

где H_i — остовные интегралы, а J_ij и K_ij — кулоновские и обменные межэлектронные интегралы, соответственно, для m-го атома. Следует всегда различать межатомные (J _mn, K _mn) и межэлектронные (J_ij, K_ij) интегралы, несмотря на сходство их названий и физической природы.

Таким образом, в основе метода ВС лежит вспомогательная структурная модель, заимствованная из классической теории химического строения, согласно которой молекула представляет собой агрегат из индивидуальных атомов, свойства которых, однако, изменены за счет межатомных взаимодействий кулоновской природы («химических связей»). Поэтому метод ВС позволяет сопоставить вводимые в его рамках поправки на межатомное взаимодействие (J _mn — межатомные кулоновские интегралы и K _mn — межатомные обменные интегралы) обычным химическим связям, которым в классической химии также приписывается локализованный бинарный характер. Это позволяет получать в квантовой химии некоторые количественные оценки таких характеристик химических связей, как длины, энергии диссоциации и др.

Вследствие больших вычислительных проблем метод ВС редко применяется в полном виде. Чаще можно встретить различные упрощенные варианты, например, т.н. полуколичественный "метод резонанса", особенно широко распространенный в органической химии.

В основе теории резонанса лежит представление метода ВС о том, что волновая функция молекулы может быть получена как суперпозиция базисных волновых функций резонансных форм.

Y _{молекулы} = С ₁ Y ₁ + С ₂ Y ₂ +... + С_n Y _n

Однако, в отличие от полного метода ВС, в теории резонанса учитывают не все базисные функции (резонансные формы), а только их небольшое число. Иначе говоря, дело сводится к "урезанию" базисного набора, что чрезвычайно упрощает математические проблемы метода ВС.

Например, для молекулы воды можно построить несколько миллионов РФ, отличающихся способом распределения 10 электронов (с учетом их спиновых состояний) по трем фрагментам разрезанной молекулы. Из них можно оставить только две группы аналогичных РФ:

Если суперпозицию волновых функций РФ распространить на сами РФ, то получится нечто среднее — т.н. "резонансный гибрид" или " мезомерная (т.е. промежуточная, усредненная) структура", в которой:

а) на атомах водорода будет наблюдаться избыточный положительный заряд (пропорциональный квадрату коэффициента С ₂);

б) на атоме кислорода будет наблюдаться избыточный отрицательный заряд (пропорциональный удвоенному квадрату коэффициента С ₂);

в) порядки ковалентных связей О—Н будут иметь величину между 1 и 0 (пропорционально квадрату коэффициента С ₁).

Основная проблема метода резонанса — рациональный отбор резонансных форм (резонансных структур). Наиболее полезным в этом отношении является правило, связывающее вклад данной РФ с ее энергией: чем выше энергия РФ, тем меньше ее вклад. Соответственно, в методе резонанса ограничиваются только теми РФ, энергии которых особенно низки. К ним относятся:

а) атомная форма (состоящая из нейтральных атомов) в которой электроны распределены в соответствии с зарядами ядер,

б) ионные формы, в которых избыточное число электронов принадлежит наиболее электроотрицательным атомам; при этом, как правило, рассматриваются только РФ с небольшими (единичными) зарядами атомов.

Дополнительно можно отметить, что часто в методе резонанса используются не полные, а частичные резонансные формы, в которых атомной локализации подвергаются не все электроны молекулы, а только некоторые из них, обладающие особенно высокой энергией. Частичная резонансная форма отличается тем, что ее можно однозначно изобразить классической структурной формулой или формулой Льюиса.

Например, молекулу диоксида углерода можно рассматривать как резонансный гибрид ковалентной и ионной форм, отличающихся локализацией подвижных электронных пар двойных связей:

Аналогично, молекула монооксида углерода представляется в виде резонансного гибрида структур, отличающихся состояниями неподеленной пары электронов кислорода и вакантной АО атома углерода:

При описании молекулы бензола можно вообще не учитывать ионные резонансные структуры, имеющие в данном случае гораздо более высокие энергии, чем ковалентные, так как в молекуле нет атомов с высокой электроотрицательностью:

Таким образом, метод резонанса позволяет использовать основные идеи метода ВС и получать без особых математических затруднений качественные или полуколичественные результаты, которые достаточны для решения многих чисто химических задач, связанных с электронным строением молекул.

Метод МО

В отличие от метода ВС, метод МО не основан на представлениях классической структурной химии, а представляет собой теорию многоэлектронного атома, распространенную на молекулы, которые рассматриваются как атомы особого типа — многоядерные. Возьмем, например, атом неона, состоящий из ядра с Z = +10 и 10-ти электронов, каждый из которых находится в своем стационарном состоянии, описываемом определенной атомной спин-орбиталью. Разделим ядро атома на три части с зарядовыми числами Z ₁ = Z ₂ = +1 и Z ₃ = +8 и разнесем эти ядерные фрагменты в пространстве на определенные расстояния. Если перемещение ядер будет сравнительно медленным (адиабатическим), то электроны не будут участвовать в каких-либо квантовых скачках, а просто будут приспосабливаться к новой конфигурации электрического поля (новой форме потенциальной ямы), оставаясь все время в стационарных состояниях. В результате такого процесса получится трехядерная молекула воды:

При таком подходе электронная оболочка молекулы считается полностью обобщенной, и каждый электрон в ее составе принадлежит только всей молекуле целиком, но не какому-либо отдельному атому. В рамках метода МО предполагается, что электроны в получившейся молекуле, так же как и в исходном атоме, находятся в стационарных состояниях, описываемых молекулярными спин-орбиталями (МСО), которые представляют собой видоизмененные (деформированные) атомные спин-орбитали (АСО).

Каждый электрон характеризуется тем же набором локальных наблюдаемых, что и в атоме: энергией (e _i), спиновым моментом (`s) и орбитальным моментом (`l). Более низкая симметрия электрического поля ядер в молекуле приводит к более сложному в пространственном отношении характеру движения электронов. Поэтому в молекулах электронам, как правило, нельзя приписать определенных значений орбитального момента (исключением являются только линейные молекулы и плоские циклические молекулы типа бензола).

Таким образом, в основе метода МО лежит утверждение, что движение каждого молекулярного электрона описывается одноэлектронной волновой функцией — МСО и набором одноэлектронных наблюдаемых:

электрон 1 Û j₁ ; e₁, | s |₁, s_{z 1}, { | l |_1, l _{z 1} }

электрон 2 Û j₂ ; e₂, | s |₂, s_{z 2}, { | l |_2, l _{z 2} }

………………………………………………..

электрон n Û j _n; e _n, | s | _n, s_zn, { | l | _{n ,} l _zn }

Подобно АСО, каждую МСО можно (пренебрегая магнитными взаимодействиями) представить в виде произведения пространственного и спинового множителей: j = y •c, причем пространственный множитель y(x, y, z) называется молекулярной орбиталью (МО). Ввиду отсутствия сферической симметрии у молекул МО представляют, как правило, в декартовой системе координат.

Связь между глобальной волновой функцией и одноэлектронными МО устанавливается так же как в атоме — посредством определителя Слэтера:

Ф = || j₁ j₂ … j _n ||

либо в виде линейной комбинации таких определителей, что иногда бывает необходимо для выделения глобального спинового множителя: Ф = Y • W.

Основная теоретическая проблема метода МО состоит в установлении явного вида МО. Найти этот вид посредством решения какого-либо уравнения на собственные значения невозможно. Поэтому для их анализа используют стандартный прием — разложение по некоторому базисному набору:

j₁ = С ₁₁y₁ + С ₁₂y₂ + … + С _{1 n} y _n

j₂ = С ₂₁y₁ + С ₂₂y₂ + … + С _{2 n} y _n

……………………………………

j _n = С_{n 1}y₁ + С_{n 2}y₂ + … + С _{n n} y _n

То же самое можно записать в матрично-векторной:

или в соответствующей операторной форме:

j = С • y.

Базисных наборов, как обычно, существует бесконечно много, и различные базисы будут, естественно, приводить к различным представлениям молекулярных орбиталей. Поэтому орбитальная модель молекулы может выглядеть по-разному, в зависимости от выбранного базиса. Наиболее широко используемым базисным набором является т.н. "атомный базис". Его, в соответствии с общим правилом квантовой механики, можно определить с помощью измерительного прибора следующей конструкции. Удалим из молекулы все электроны, кроме одного. Затем поместим ядерный остов молекулы в ящик с перегородками так, чтобы каждое ядро попало в свой отсек. В ходе такого "измерения" электрон случайным образом будет обнаруживаться в одном из "атомных" отсеков и ему можно будет приписать номер того ядра, в чей отсек он попал.

Таким образом, базисное состояние y _i — это такое состояние, когда электрон вынужден двигаться в окрестности единственного ядра, подобно тому, как это имеет место в атоме. Однако такие базисные состояния несколько отличаются от атомных орбиталей изолированных атомов, поскольку электрон находится под влиянием электрических сил со стороны всех ядер молекулярного остова. Влиянием удаленных ядер часто пренебрегают и полагают, что базисные состояния y _i описываются обычными АО. Поэтому описанный способ конструирования МО называется ЛКАО (линейная комбинация атомных орбиталей). Оператор С в этом случае называется атомно-молекулярным оператором, так как он преобразует орбитали от их атомной формы к молекулярной.

После выбора базисного набора остается проблема определения коэффициентов разложения С_ij (матричных элементов атомно-молекулярного оператора С). Решение этой задачи облегчается тем, что на коэффициенты С_ij накладывается ряд ограничений.

а) МО должны удовлетворят стандартному условию ортонормированности:

òj _i j _j dV = d _ij

б) каждая МО должна иметь определенную пространственную симметрию, в соответствии с симметрией ядерного остова, а именно: принадлежать одному из неприводимых представлений точечной группы симметрии молекулы

j _i Î НП ТГС,

поскольку только в этом случае электронное облако, форма которого определяется квадратом МО, будет соответствовать форме самой молекулы.

После анализа и учета указанных ограничений коэффициенты С_ij определяются посредством обычной процедуры самосогласования. Для этого:

1) выбирают электронную конфигурацию,

2) выражают каждую МО в виде ЛКАО,

3) выражают полную энергию через молекулярные орбитали, в результате чего она получается в виде функции от коэффициентов Е = F (С_ij),

4) дифференцируют эту функцию по коэффициентам и приравнивают производные к нулю: ¶ Е /¶ С_ij = 0.

Получаемая система уравнений (содержащая n ´ n уравнений), называется уравнениями Хартри-Фока-Рутана (ХФР). Она состоит из n одинаковых экземпляров системы из n уравнений следующего вида:

где F _mn — матричные элементы оператора Фока, характеризующие либо энергию электрона в изолированном атоме с номером m (при m = n), либо изменение энергии электрона при его обобществлении двумя атомами с номерами m и n (при m ¹ n), S _mn — интегралы перекрывания для базисных АО с номерами m и n, а e — энергия МО с коэффициентами { С _a С _b.. С_n }.

Основные проблемы метода МО связаны с необходимостью процедуры самосогласования, включающей многократные вычисления интегралов типа F и S. Идея решения сводится к следующему. Всякая система однородных линейных уравнений имеет решение только в том случае, если ее определитель равен нулю. Приравнивание определителя системы ХФР к нулю дает характеристическое уравнение относительно e, имеющее n корней: e₁, e₂, …, e _n. Подставляя поочередно эти корни в систему, находят n решений, каждое из которых представляет собой набор коэффициентов для одной из МО. Найденные коэффициенты используют для вычисления матричных элементов F и S и повторяют процедуру решения.

После достижения заданной точности получают самосогласованное решение в виде набора МО и их энергий:

j₁^* j₂^* … j _n ^*

e₁^* e₂^* … e _n ^*

Такой подход к решению системы ХФР носит называние "метод ab initio " и отличается тем, что в нем все интегралы F и S рассчитываются в ходе решения уравнений ХФР. Существуют и альтернативные методы, которые называются полуэмпирическими, так как в них часть или даже все интегралы F и S находятся из эмпирических данных (например, спектральных). Это позволяет значительно снизить число итераций и ускорить процедуру решения. Полуэмпирических методов существует чрезвычайно много, причем все они дают несколько различные результаты.

Оператор Гамильтона в методе МО строят в виде:

H = å (T _i) + åå (U _{i m}) + åå (U _ij) + åå (U _mn) = å (h _i) + åå (U _ij)

где T _i = (–h²/2 m)Ѳ _i — оператор кинетической энергии i -го электрона,

U _{i m} = – Z _m e ²/ r_{i m} — оператор потенциальной энергии i -го электрона в кулоновском поле m-го ядра,

U _ij = e ²/ r_ij — операторы межэлектронного отталкивания,

h _i = T _i + å (U _{i m}) — т.н. "одноэлектронные гамильтонианы".

Поэтому полная энергия молекулы в методе МО задается в виде суммы орбитальных энергий с поправками на межэлектронное взаимодействие:

Е = å e _i ^* + åå (J_ij ± K_ij)

где J_ij — кулоновские интегралы, а K_ij — обменные интегралы (их физический смысл тот же, что и в теории МЭА).

В большинстве случаев наилучших результатов удается достичь, если использовать многодетерминантные волновые функции, каждая из которых соответствует своей электронной конфигурации. Выигрыш в энергии, достигаемый за счет перехода от однодетерминантной волновой функции к многодетерминантной приписывается действию т.н. "конфигурационного взаимодействия" (КВ). Следует иметь в виду, что КВ — это не особый вид физического взаимодействия, а всего лишь способ введения поправок в волновую функцию молекулы и ее энергию.

Важное место в описании молекул методом МО занимают энергетические диаграммы, изображающие графически совокупность молекулярных орбиталей в отношении их расположения на энергетической шкале. Указание заселенностей этих орбиталей (энергетических уровней) приводит к такой характеристике молекулы, как ее электронная конфигурация, смысл которой аналогичен электронной конфигурации атома. Наряду с энергетическими, широко используются и т.н. корреляционные диаграммы, представляющие собой совместное изображение энергетических диаграмм электронных состояний атомного (y _i) и молекулярного (j _i) типов.

Такие диаграммы позволяют проследить характер изменения состояния каждого электрона и изменения в его энергии при образовании молекулы из "атомов".

Канонические МО

Молекулярные орбитали, находимые как решения уравнений ХФР, называются каноническими (КМО). Их отличительная черта — полная делокализованность. Другими словами, каждая КМО распространяется на всю молекулу в целом, что отражает тот факт, что любой электрон молекулы может быть найден в любой точке внутри молекулярного объема. КМО, помимо их энергии, могут быть охарактеризованы и с пространственной точки зрения, аналогично атомным орбиталям.

Наиболее важными из пространственных характеристик КМО являются:

1) узловая структура, т.е. совокупность узловых поверхностей, разделяющих объем молекулы на части, и на которых КМО и вероятность обнаружения электрона равна нулю; здесь выполняется общее квантово-механическое правило — число узлов КМО пропорционально орбитальное энергии;

2) пространственная симметрия, которую можно описать, указав неприводимое представление (тип симметрии) точечной группы молекулы; например, все КМО молекулы воды должны иметь один из четырех типов симметрии группы С_2v, а все КМО молекулы метана — один из пяти типов симметрии группы T_d.

Например, в молекуле бутадиена имеется 4 КМО такой формы:

Из рисунков видно, что первая КМО является безузловой, вторая имеет один узел, третья — два узла, а четвертая — три. Соответственно, симметрия этих КМО описывается НП группы С_2v: первая и третья КМО принадлежат типу В₂ (антисимметричны относительно операции С₂) а вторая и четвертая — типу А₂ (симметричны относительно операции С₂).

Симметрия часто используется для классификации МО. Так, для плоских молекул имеется операция отражения в плоскости молекулы. Соответственно, МО может быть либо симметричной, либо антисимметричной, относительно этой операции. В поперечном разрезе такие МО имеют следующий вид:

Локальные характеристики молекулы в методе КМО

Знание коэффициентов МО позволяет рассчитывать некоторые полезные характеристики молекулы, имеющие локальный характер — отнесенные к отдельным атомным фрагментам в составе молекулы. Расчет основан на матричном представлении коэффициентов КМО:

Каждая строка матрицы коэффициентов соответствует определенной КМО, т.е. некоторому электрону. Каждый столбец матрицы соответствует определенному атому молекулы, и коэффициенты, входящие в этот столбец, показывают вклад отдельных электронов в свойства атома. В частности, квадрат коэффициента С_ik дает вероятность нахождения электрона с номером i в окрестности атома с номером k, или, другими словами, электронную плотность на атоме с номером k, создаваемую электроном с номером i.

Электронная плотность атомов

Для расчета электронной плотности атома следует просто просуммировать такие плотности по всем электронам молекулы. Отсюда получается простая формула:

где C_{i n} — коэффициент МО с номером i при атоме с номером n,

k_i — заселенность данной МО (число электронов).

Кроме средней электронной плотности, рассчитываемой по данной формуле, каждый атом можно охарактеризовать еще одним числом n ^o, которое равно числу электронов, поставляемых данным атомом в общую электронную оболочку молекулы. Тогда разность между этим числом и реальной электронной плотностью будет представлять собой избыточный электрический заряд, локализованный в области пространства молекулы, занимаемой данным атомом:

Порядок химической связи

Порядок связи между парой атомов пропорционален величине электронной плотности в пространстве между соответствующими атомными ядрами. В свою очередь, электронная плотность определяется интерференционным эффектом для пары перекрывающихся АО. Этот эффект может быть конструктивным, когда перекрывающиеся АО имеют один и тот же знак (перекрывание "в фазе"), или деструктивным, когда перекрывающиеся АО имеют разные знаки (перекрывание "в противофазе"). В первом случае электрон, заселяющий МО, создает избыток отрицательного заряда в пространстве между ядрами, что приводит к появлению сил притяжения. Во втором случае между ядрами появляется узловая поверхность и электрон, заселяющий МО, вызывает отталкивание между ядрами.

В результате, порядок связывания между атомами, обусловленный электроном, заселяющим некоторую МО, пропорционален произведению коэффициентов этой МО при базисных АО, соответствующих данным атомам. Следовательно, для заданной пары атомов с номерами n и m порядок связи может быть рассчитан по формуле:

Индекс свободной валентности.

­Индекс свободной валентности некоторого атома молекулы рассчитывается по формуле:

I _n = N _max – P _n

где N _max — некоторая калибровочная константа (для атомов углерода она, обычно принимается равной 4,732), а P _n — сумма порядков всех связей, которые атом с номером n образует со своими соседями.

Результаты расчета молекулярных характеристик принято выражать в виде т.н. ”молекулярной диаграммы”, представляющей собой топологический граф молекулы, снабженный значениями зарядов атомов, порядков связей и индексов свободной валентности. В качестве примера приведем молекулярную диаграмму фульвена. Пользуясь молекулярной диаграммой, можно получить множество полезных сведений о свойствах молекул. Так, например, для молекулы фульвена мы видим, что эта молекула поляризована, несмотря на то, что ее скелет состоит из одинаковых атомов углерода.

Для отображения такой поляризации часто изображают структуру фульвена в виде резонанса между двумя крайними (резонансными) формами:

Кроме того, можно встретить и другой способ описания молекулярных характеристик — в виде т.н. "PQ-матрицы" (матрицы зарядов и порядков). Это квадратная матрица, размером (n ´ n), причем по диагонали ее располагаются электронные плотности атомов (иногда — заряды атомов), а недиагональным элементам соответствуют порядки связей для данной пары атомов:

Возможность построения такой матрицы обусловлена использованием одинаковой расчетной формулы и для электронных плотностей атомов и для порядков связей. Эти формулы были предложены Коулсоном, и матрица поэтому часто называется "матрицей Коулсона". Очевидно, что рассмотренные расчетные формулы имеют конвенциональный характер и могут быть изменены. Действительно, существует и ряд других определений для величин, называемых "электронная плотность атома" и "порядок связи", приводящих к другим численным значениям. В качестве примера приведем т.н. "матрицу Малликена":

Здесь величины S _nm представляют собой интегралы перекрывания, а величины x_i — собственные числа т.н. "топологической" матрицы.

Поляризуемости.

Введем два типа параметров, характеризующих атомы и связи в молекуле.

1) остовный интеграл a _r, равный энергии электрона, локализованного на АО данного атома молекулы с номером r (абсолютная величина этого интеграла пропорциональна электроотрицательности атома);

2) резонансный интеграл b _rs, равный энергетическому эффекту делокализации электрона (абсолютная величина этого интеграла пропорциональна прочности химической связи между атомами):

В результате, молекула будет характеризоваться набором локальных атомных (a₁, a₂, …, a _n) и связевых (b₁₂, b₂₃, …) параметров, которые определяют собой характер распределения электронной плотности в молекуле, т.е. заряды атомов (q_r) и порядки связей (P_rs). В частности, выполняются следующие соотношения:

` n_r = ¶ E / ¶a _r и P_rs = (1/2) ¶ E / ¶b _rs

где Е — полная электронная энергия молекулы.

Более отрицательные значения остовных интегралов соответствуют более высокой электронной плотности. Например, в молекуле HCl электронная плотность выше на атоме хлора, которому соответствует более отрицательное значение интеграла a. Более отрицательные значения резонансного интеграла соответствуют более высоким порядкам связей, т.е. сосредоточению электронной плотности в промежутках между соответствующими атомами.

С помощью интегралов a и b удобно описывать различные внешние возмущения, которые носят локальный характер, т.е. направлены и влияют на отдельные атомы и связи (пары атомов). Такие возмущения могут возникать за счет химических изменений в молекуле (например, замещение одного атома на другой), взаимодействия с молекулами реагентов, молекулами растворителя, активными центрами катализатора и т.д. Предполагается, что эти возмущения приводят к изменению интегралов a и b, и как следствие — к перераспределению электронной плотности в молекуле, т.е. к изменениям значений зарядов атомов (q_r) и порядков связей (P_rs).

Поляризуемости представляют собой количественные оценки степени восприимчивости (чувствительности) молекулы к внешним возмущениям.

Дата добавления: 2015-07-20