
|
Читайте также: |
Последовательностные устройства этого типа называют также распределителями сигналов, так как последовательность двоичных чисел на их выходах используется для управления работой других цифровых узлов. Число состояний генератора называется длиной последовательности чисел Ln, которая равна количеству тактов, после которого последовательность чисел на выходе генератора повторяется.
По своей структуре генераторы чисел близки либо к счетчикам, либо к регистрам.
Генераторы на основе счетчиков. Любой счетчик можно считать генератором последовательности чисел, имеющей Ln = Kсч. Как правило, требуемое число разрядов генератора равно числу двоичных разрядов m в генерируемых числах. Если m > log2 Ln, то для уменьшения числа используемых триггеров структура генераторов изменяется. В этом случае генератор целесообразнее строить в виде счетчика с модулем счета Kс = Ln и подключенной к его выходам комбинационной схемой (КС), синтезирующей требуемые значения двоичных чисел последовательности.
В качестве примера рассмотрим генератор чисел 3 – 2 – 12 – 4. Так как Ln = 4, то за основу генератора можно взять двухразрядный счетчик с Kсч. = 4, который генерирует числа 0 – 1 – 2 – 3. Подключив к выходам счетчика КС, выполняющую преобразование кодов в соответствии с табл. 14, получим структуру генератора, образующего заданную последовательность чисел (рис. 52).

Рис. 52. Генератор числовой последовательности на основе счетчика с выходной комбинационной схемой
Временная диаграмма работы такого генератора приведена на рис. 53

Рис. 53. Временная диаграмма работы генератора
Проектирование такого генератора по обычной методике проектирования недвоичных счетчиков потребовало бы в два раза больше счетчиков и дополнительной логики.
Генераторы на основе сдвиговых регистров. В генераторах такого типа каждое последующее число последовательности образуется путем сдвига предыдущего числа на один разряд вправо и введением в освободившийся первый разряд нуля или единицы. Такие последовательности называются циклическими.
Основой генератора является сдвиговый регистр с входной комбинационной схемой, вырабатывающий управляющий сигнал z0 для установки первого разряда. Если имеется m-разрядный сдвиговый регистр, то с его помощью можно получить последовательности длиной Ln Ј 2m.
Построив граф состояний (рис. 54), например, трехразрядного регистра со сдвигом вправо, показывающий все возможные переходы при вводе в первый разряд нуля или единицы, можно увидеть, что число реализуемых последовательностей чисел будет весьма значительно.
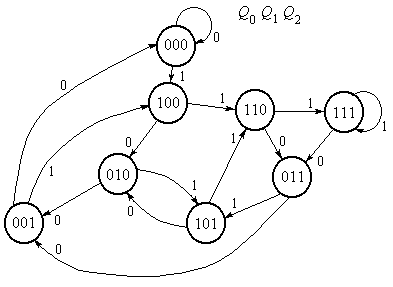
Рис. 54. Возможные графы переходов трехразрядного регистра
В кружках графа указаны состояния выходов регистра, строками обозначены возможные переходы состояний регистра при изменении младшего разряда. Если очередной переход не изменяет состояния регистра, то стрелка замыкается на исходном состоянии.
Синтез структуры генераторов последовательностей на сдвиговых регистрах, в первую очередь, состоит в нахождении вида функции z0.
Рассмотрим это на примере синтеза генератора последовательности
0 – 1 – 3 – 7 – 6 – 5 – 2 – 4.
1. Составляется таблица переходов состояний разрядов регистра (табл. 15).
Таблица 15
| Номер состояния | Q2n | Q1n | Q0n | Q2n+1 | Q1n+1 | Q0n+1 |
2. Составляются карты Карно для переходов триггера первого разряда и его функции входов z0. Обычно, в сдвиговых регистрах используются D-триггеры, поэтому z0 = D0 (рис. 55)

Рис. 55. Карты Карно для триггера первого разряда
3. Находится значение функции D0:
 .
.
4. Составление логической схемы генератора выполняется построением управляющей комбинационной схемы, реализующей функцию входов D0, и ее подключением ко входу первого разряда сдвигового регистра (рис. 56)

Рис. 56. Логическая схема генератора последовательности на основе регистра
Синтезировав комбинационную схему с перестраиваемой структурой, можно получить ряд различных последовательностей от одного устройства.
Генераторы на основе регистров образуют только циклические последовательности чисел. Для реализации любых нециклических последовательностей требуется использование дополнительных комбинационных преобразователей кодов, включаемых на выходе генератора.
Порядок появления чисел в последовательности можно считать случайным, а повторение чисел происходит через 2m – 1 тактов, поэтому такие схемы называются генераторами псевдослучайных последовательностей. При увеличении m длина псевдослучайных последовательностей быстро возрастает, поэтому генераторы, имеющие m > 10, широко используются в цифровой аппаратуре для формирования множества тестовых сигналов, необходимых для контроля и диагностики неисправностей.
Дата добавления: 2015-07-11; просмотров: 727 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Последовательные регистры | | | Интеграция: сущность, причины, виды, последствия |