Сварка меди и медных сплавов

Медь используют в химическом и энергетическом машиностроении ввиду высокой электро- и теплопроводности, высокой коррозионной стойкости в некоторых агрессивных средах. Все эти свойства тем выше, чем выше чистота металла, что предъявляет особые требования к сварке изделий из чистой меди. Сварка бронз и латуней имеет свои особенности, но свойства чистой меди в этих сплавах уже значительно утрачены.

В зависимости от количественного содержания примесей, различают пять основных марок технической меди: М0 – с суммарным содержанием примесей не более 0,05%, М1 – не более 0,10%, М2 – не более 0,30%, М3 – не более 0,50% и М4 – с содержанием примесей не более 1,00%.

8. Проводниками называются вещества, внутри которых в случае электростатического равновесия электрическое поле равно нулю, т.е. некомпенсированные заряды проводников локализуются в бесконечно тонком поверхностном слое, а если электрическое поле отлично от нуля, то в проводнике возникает электрический ток.

Проводниковые свойства проявляют как твердые тела, так и жидкости, а при соответствующих условиях и газы.

В электротехнике из твердых проводников наиболее широко используются металлы и их сплавы, различные модификации проводящего углерода и композиции на их основе.

Металлические проводниковые материалы подразделяются на материалы высокой проводимости и сплавы высокого сопротивления. Металлы высокой проводимости используются в тех случаях, когда необходимо обеспечить минимальные потери передаваемой по ним электрической энергии, а сплавы высокого сопротивления, наоборот, в тех случаях, когда необходима трансформация электрической энергии в тепловую.

К жидким проводникам относятся расплавы и электролиты. Если при прохождении тока через жидкие проводники на электродах не происходит выделение продуктов электролиза, то они относятся к проводникам первого рода. Расплавы ионных кристаллов и электролиты относятся к проводникам второго рода, так как при прохождении через них тока происходит перенос вещества, а на электродах выделяются продукты электролиза.

Газы и парообразные вещества становятся проводниками лишь в определенных диапазонах значений давления, температуры и напряженности электрического поля. Близка к газам по своему агрегатному состоянию особая проводящая среда — плазма.

К особой группе проводящих материалов относятся сверхпроводники.

Современная теория проводников основывается на постулатах квантовой механики. В рамках этой теории предполагается, что при отсутствии внешних воздействий (электрические и магнитные поля, градиент температуры) система подвижных электрических зарядов в проводниках описывается равновесной функцией распределения. Реакция на любое внешнее воздействие, нарушающее равновесное состояние подвижных зарядов, может быть описана с помощью неравновесной функции распределения, конкретный вид которой зависит от типа воздействия и определяется на основе решения кинетического уравнения Больцмана. Количественная связь между внешним воздействием и реакцией на него подвижных носителей заряда описывается с помощью кинетических коэффициентов, из которых наиболее важную практическую роль играют коэффициент электрической проводимости (выражает связь между напряженностью электрического поля в проводнике и плотностью тока) и коэффициент тепловой проводимости (выражает связь между разностью температур на единичной длине проводника и тепловым потоком). Математически эти явления описываются законами Ома и Фурье: 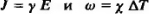, где Е — напряженность электрического поля, В/м; J — плотность тока, А/м; ω — плотность теплового потока, Вт/м; ΔT — разница температур на единичном участке длины проводника, К/м; γ — коэффициент электрической проводимости (удельная электрическая проводимость), См/м; χ — коэффициент теплопроводности, Вт/(м · К).

При наличии градиентов температуры и потенциала в одном или нескольких соединенных проводниках возникает ряд термоэлектрических эффектов. Самые важные из них — эффекты Зеебека, Пельтье и Томсона. Если градиент температуры вдоль проводника не равен нулю, то на его концах появляется разность потенциалов, называемая термоэлектрической разностью потенциалов, или термоэлектродвижущей силой. При разности температур в 1 К эта разность потенциалов называется удельной (дифференциальной) термоэлектродвижущей силой. В разомкнутой цепи из нескольких разнородных проводников, находащихся при одинаковой температуре, появляется контактная разность потенциалов, равная алгебраической сумме разностей работ выхода электронов из проводников. При замыкании такой цепи ток не возникает, так как контактные разности потенциалов компенсируют друг друга. Если же поддерживать контакты при разных температурах, возникает отличная от нуля термоэлектродвижущая сила, называемая (при разности температур в 1 К) относительной удельной термоэлектродвижущей силой. По имени физика, изучавшего это явление, оно получило название эффекта Зеебека. Этот эффект, положенный в основу работы промышленных термопар, наиболее изучен. Эффект Пельтье состоит в выделении обратимого тепла на контакте двух различных проводников, когда через контакт проходит ток. Эффект Томсона состоит в выделении обратимой теплоты, когда в проводнике протекает ток при наличии градиента температуры.

При одновременном воздействии на проводник электрического и магнитного полей возникают гальваномагнитные эффекты

Наиболее полно к настоящему времени развита теория металлических проводников. Еще на рубеже XIX—XX вв теоретически и экспериментально было показано, что если металл находится в твердом или жидком состоянии, то часть электронов делокализуется, а возникающие в результате этого положительно заряженные ионы образуют (если металл находится в твердом состоянии) кристаллическую решетку. Взаимодействие положительно заряженного остова кристаллической решетки с делокализованными электронами обеспечивает стабильность и устойчивость структуры металлов, а наличие электронов, принадлежащих не отдельным атомам, а всей их совокупности, обеспечивает высокую электрическую проводимость металлов. Однако наиболее точные расчеты кинетических коэффициентов получены на основе современной теории металлов, в которой совокупность делокализованных электронов рассматривается как «Ферми-жидкость», подчиняющаяся статистике Ферми. Наибольшую практическую ценность представляют результаты теоретического исследования электрической проводимости металлов.

В современной теории электропроводности показано, что в идеальной кристаллической решетке электрический или тепловой поток, однажды возникнув, поддерживался бы бесконечно долго, т.е. делокализованные электроны создавали бы бесконечную проводимость, а время релаксации (среднее время свободного пробега электронов) оказалось бы бесконечным. Тот факт, что удельная электрическая проводимость конечна, обусловлен нерегулярностями решетки. Эти нерегулярности делятся на две основные категории. Одни связаны с тепловыми колебаниями, другие являются статистическими. Тепловые колебания решетки нарушают идеальную периодичность кристаллов. Искажения решетки рассеивают электроны, ограничивая длину свободного пробега конечным значением. С уменьшением температуры интенсивность рассеивания уменьшается, и так как ограничения, налагаемые статистикой Ферми, препятствуют рассеянию на нулевых колебаниях, то в области температур, близких к абсолютному нулю, проводимость ограничивается статическими дефектами. Обычно существует целый ряд статических дефектов. Вакансии, междуузельные атомы и примеси замещения составляют группу точечных дефектов. Дислокации являются линейными дефектами. Существуют и двумерные нерегулярности, такие как дефекты упаковки и границы двойников и кристаллитов.

В итоге теория предсказывает, а эксперимент подтверждает, что в области низких температур (меньших температуры Дебая Θ) удельная электропроводность γ пропорциональна T^-5, а при T>Θ γ ~ T^-1, где T — температура перехода.

В практике проведения электротехнических расчетов часто используется не удельная проводимость, а величина, ей обратная, ρ (Ом·м). Учитывая это, ρ~Т при T>Θ. Для большинства металлов температура Дебая лежит в области от 100 до 400 К.

В технических расчетах влияние температуры на сопротивление характеризуют температурным коэффициентом удельного сопротивления .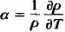

В настоящем справочнике приводится средняя величина α, которая позволяет приближенно определить ρ при произвольной температуре 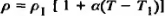. где ρ₁ — удельное сопротивление при температуре T₁.

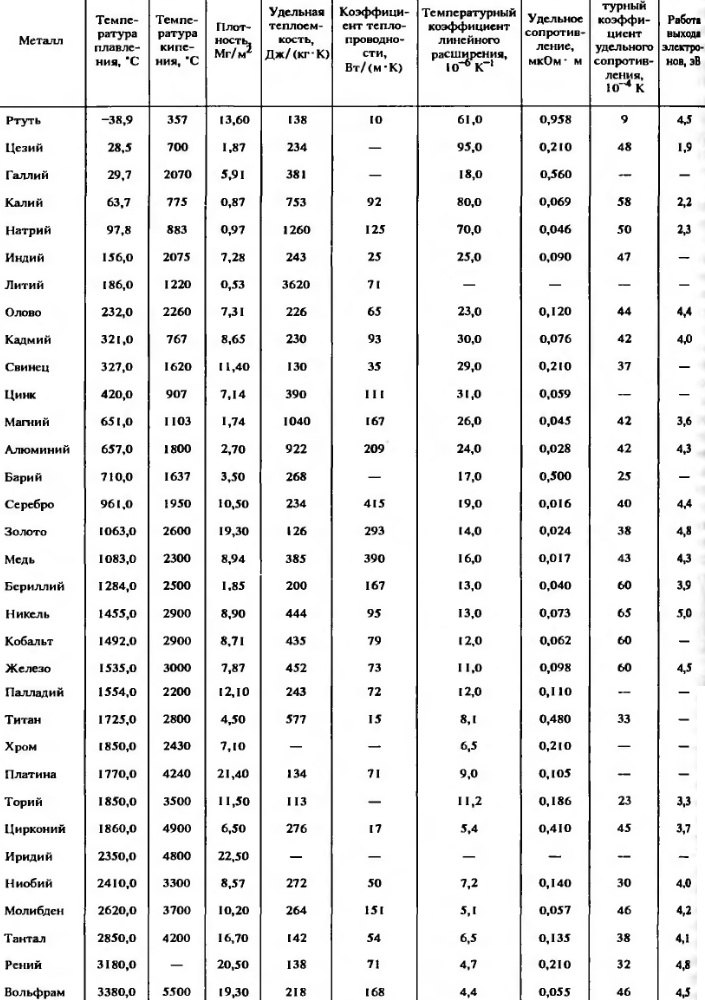
Основные физические свойства металлов приведены в табл. 1.

9. Общие сведения о проводниках

В качестве проводников электрического тока могут быть использованы как твердые тела, так и жидкости, а при соответствующих условиях (в состоянии ионизации) и газы.

Из металлических проводниковых материалов могут быть выделены металлы высокой проводимости, имеющие удельное сопротивление при нормальной температуре не более 0.05 мкОм·м, и сплавы высокого сопротивления с удельным сопротивлением не менее 0.3 мкОм·м.

Особый интерес представляют обладающие чрезвычайно малым удельным сопротивлением при весьма низких температурах материалы сверхпроводники и криопроводники.

К жидким проводникам относятся расплавленные металлы и электролиты. Для большинства металлов температура плавления высока, только ртуть, имеющая температуру плавления минус 39°С, может быть использована в качестве жидкого металлического проводника при нормальной температуре. Другие металлы являются жидкими проводниками только при повышенных температурах.

Механизм прохождения тока в металлах – как в твердом, так и в жидком состоянии – обусловлен движением свободных электронов под воздействием электрического поля; поэтому металлы называют проводниками с электронной электропроводностью или проводниками первого рода. Проводниками второго рода, или электролитами, являются растворы, в частности, водные, кислот, щелочей и солей. Прохождение тока через эти вещества связано с переносом вместе с электрическими зарядами ионов в соответствии с законами Фарадея, вследствие чего состав электролита постепенно изменяется, а на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном состоянии также являются проводниками второго рода. Пример – соляные закалочные ванны с электронагревом.

Все газы и пары, в том числе и пары металлов, при низких напряженностях электрического поля не являются проводниками. Однако, если напряженность поля превзойдет некоторое критическое значение, обеспечивающее начало ударной и фотоионизации, то газ может стать проводником с электронной и ионной проводимостью. Сильно ионизированный газ при равенстве числа электронов числу положительно заряженных ионов в единице объема представляет собой особую проводящую среду, называемую плазмой.

2.2. Электропроводность металлов

Классическая электронная теория металлов представляет проводник в виде системы, состоящей из узлов ионной кристаллической решетки, внутри которой находится электронный газ из свободных электронов. В свободное состояние от каждого атома переходит от одного до двух электронов. К электронному газу применялись представления и законы статистики обычных газов. Рассматривая тепловое и направленное под действием электрического поля движение электронов, получили выражение закона Ома. При столкновениях электронов с узлами кристаллической решетки энергия, накопленная при ускорении электронов в электрическом поле, передается металлической основе проводника, вследствие чего он нагревается. Рассмотрение этого роцесса привело к выводу закона Джоуля-Ленца. Т.о., электронная теория металлов дала возможность теоретически описать и объяснить найденные ранее экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах. Оказалось возможным также объяснить связь между электро- и теплопроводностью металлов.

Однако появились и противоречия некоторых выводов теории с опытными данными. Они состояли в расхождении кривых температурной зависимости удельного сопротивления, в несоответствии теоретически полученных значений теплоемкости металлов опытным данным.

Эти трудности удалось преодолеть, встав на позиции квантовой механики. В отличие от классической электронной теории квантовая механика полагает, что электронный газ в металлах при обычных температурах находится в состоянии вырождения. В этом состоянии энергия электронного газа почти не зависит от температуры, т.е. тепловое движение почти не изменяет энергию электронов. Поэтому теплота не затрачивается на нагрев электронного газа, что и обнаруживается при измерениях теплоемкости металлов. В состояние, аналогичное обычным газам, электронный газ приходит при температурах порядка тысяч Кельвинов. Представляя металл как систему, в которой положительные ионы скрепляются посредством свободно движущихся электронов, легко понять природу всех основных свойств металлов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.

2.3. Свойства проводников

К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
-удельная проводимость g или обратная ей величина – удельное сопротивление r,
-температурный коэффициент удельного сопротивления ТКr или a_r,
-теплопроводность g _т,
-контактная разность потенциалов и термо-э.д.с.,
-работа выхода электронов из металла,
-предел прочности при растяжении s_r и относительное удлинение при разрыве Dl/l.

2.3.1. Удельная проводимость и удельное сопротивление проводников

Связь плотности тока J, А/м², и напряженности электрического поля Е, В/м, в проводнике дается известной формулой:

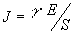(2.1)

Здесь g, См/м – параметр проводникового материала, называемый его удельной проводимостью; в соответствии с законом Ома g не зависит от напряженности электрического поля при изменении последней в весьма широких пределах. Величина r=1/g, oбратная удельной проводимости и называемая удельным сопротивлением, для имеющего сопротивление R проводника длиной l с постоянным поперечным сечением S вычисляется по формуле

ρ = R·S/l. (2.2)

Единица СИ для удельного сопротивления - Ом·м. Диапазон значений удельного сопротивления ρ металлических проводников при нормальной температуре довольно узок: от 0.016 для серебра и до примерно 10 мкОм·м для железохромоалюминиевых сплавов, т.е. он занимает всего три порядка. Значение удельной проводимости γ в основном зависит от средней длины свободного пробега электронов в данном проводнике, которая, в свою очередь, определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению ρ. И с точки зрения волновой теории, рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины электронной волны. Нарушения меньших размеров не вызывают заметного рассеяния волн.

2.3.2. Температурный коэффициент удельного сопротивления металлов

Число носителей заряда в металлическом проводнике при повышении температуры остается практически неизменным. Однако вследствие колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного под действием электрического поля движения свободных электронов, т.е. уменьшается средняя длина свободного пробега электрона, уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов, и увеличивается удельное сопротивление. Иными словами, температурный коэффициент удельного сопротивления металлов положителен.

2.3.3.Изменение удельного сопротивления металлов при плавлении

При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления, как это видно из рис.2.1; однако некоторые металлы при плавлении повышают ρ.

Рис.2.1.Зависимость удельного сопротивления меди от температуры.

Скачок соответствует температуре плавления меди 1083°С

Удельное сопротивление увеличивается при плавлении у тех металлов, которые при плавлении увеличивают объем, т.е. уменьшают плотность; у металлов с противоположным характером изменения объема при плавлении (аналогичным фазовому переходу лед-вода) ρ уменьшается.

2.3.4. Изменение удельного сопротивления металлов при деформациях

Изменение удельного сопротивления при растяжении или сжатии приближенно может оцениваться формулой

ρ = ρ₀ (1± σ ·s), (2.3)

где ρ - удельное сопротивление металла при механическом напряжении σ, ρ₀ – удельное сопротивление металла, не подверженного механическому воздействию, s – коэффициент механического напряжения, характеризующий данный металл; знак плюс в формуле соответствует растяжению, минус – сжатию.

Изменение ρ при упругих деформациях объясняется изменением амплитуды колебаний узлов кристаллической решетки металла. При растяжении эти амплитуды увеличиваются, при сжатии – уменьшаются. Увеличение амплитуды колебаний узлов кристаллической решетки приводит к уменьшению подвижности носителей зарядов и, как следствие, к возрастанию ρ. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем отжига удельное сопротивление может быть вновь снижено до первоначального значения.

2.3.5. Удельное сопротивление сплавов

Значительное возрастание ρ наблюдается при сплавлении двух металлов в том случае, если они образуют друг с другом твердый раствор, т.е. создают при отвердевании совместную кристаллизацию, и атомы одного металла входят в кристаллическую решетку другого. ρ имеет максимум, соответствующий некоторому определенному соотношению между содержанием компонентов в сплаве. Так, Н.С.Курнаков открыл, что в тех случаях, когда при определенном соотношении между компонентами они образуют друг с другом явно выраженные химические соединения (интерметаллиды), на кривых ρ в функции состава наблюдаются изломы (рис.2.2).

Рис. 2.2 Зависимость удельного сопротивления
сплавов цинк – магний от состава.
Точка 1 соответствует чистому Mg, 2 – соединению
MgZn, 3 - Mg₂Zn₃,., 4 – MgZn₄ 5 – MgZn₆, 6 – чистому Zn.

Исследования А.Ф.Иоффе показали, что многие интерметаллиды являются не веществами с металлическим характером электропроводности, а электронными полупроводниками.

Если же сплав двух металлов создает раздельную кристаллизацию, и структура застывшего сплава представляет собой смесь кристаллов каждого из компонентов (т.е. искажение кристаллической решетки каждого компонента не имеет места), то удельная проводимость γ сплава меняется с изменением состава приблизительно линейно, т.е. определяется арифметическим правилом смешения (рис.2.3).

Рис.2.3.Зависимость удельной проводимости сплавов медь – вольфрам от состава (в процентах по массе)

2.3.6. Теплопроводность металлов

За передачу тепла через металл в основном ответственны те же свободные электроны, которые определяют и электропроводность металлов, и количество которых в единице объема весьма велико. Поэтому, как правило, теплопроводность γ_т металлов намного больше, чем теплопроводность диэлектриков. Очевидно, что при прочих равных условиях, чем больше удельная электрическая проводимость γ металла, тем больше должна быть и его теплопроводность. Легко также видеть, что при повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость уменьшаются, отношение γ_т/γ δолжно возрастать.

Чистота и характер механической обработки металла могут заметно сказываться на его теплопроводности, в особенности при низких температурах.

2.3.7. Термоэлектродвижущая сила

При соприкосновении двух металлических проводников между ними возникает контактная разность потенциалов. Причина ее появления заключается в различии значений работы выхода электронов из различных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной теории металлов следует, что контактная разность потенциалов между металлами А и В равна:

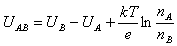(2.4)

где U_А и U_В – потенциалы соприкасающихся металлов; n_А и n_В – концентрации электронов в металлах А и В.

Если температуры "спаев" одинаковы, то сумма разностей потенциалов равны нулю. Иначе обстоит дело, когда один металл имеет температуру Т₁, а другой – Т₂.

В этом случае между "спаями" возникает термо-э.д.с., равная

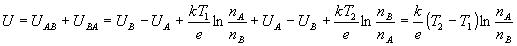(2.5)

что можно записать в виде

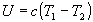(2.6)

Где с – постоянный для данной пары проводников коэффициент термо-э.д.с., т.е. термо-э.д.с. должна быть пропорциональна разности температур металлов.

Провод, составленный из двух изолированных друг от друга проволок из различных металлов или сплавов (термопара), может быть использован для измерения температур.

2.3.8. Механические свойства проводников

Они характеризуются пределом прочности при растяжении σ_р и относительным удлинением при разрыве Δl/l, а так же хрупкостью, твердостью и тому подобными свойствами. Механические свойства металлических проводников в большой степени зависят от механической и термической обработки, от наличия легирующих примесей и т.п. Влияние отжига приводит к существенному уменьшению σ_р и увеличению Δl/l. Такие параметры проводниковых материалов, как температуры кипения и плавления, удельная теплоемкость и др., не требуют особых пояснений.

10.нет

11. Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Известны несколько десятков чистых элементов, сплавов и керамик, переходящих в сверхпроводящее состояние. Сверхпроводимость — квантовое явление. Оно характеризуется также эффектом Мейснера, заключающимся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

Открытие в 1986—1993 гг. ряда высокотемпературных сверхпроводников (ВТСП) далеко отодвинуло температурную границу сверхпроводимости и позволило практически использовать сверхпроводящие материалы не только при температуре жидкого гелия (4.2 К), но и при температуре кипения жидкого азота (77 К), гораздо более дешевой криогенной жидкости.

Криопроводники.

Некоторые металлы могут достигать при низких (криогенных) температурах весьма малого значения удельного электрического сопротивления р, которое в сотни и тысячи раз меньше, чем удельное электрическое сопротивление при нормальной температуре. Материалы, обладающие такими свойствами, называют криопро-водниками (гиперпроводниками).

Физически явление криопроводимости не сходно с явлением сверхпроводимости. Плотность тока в криопроводниках при рабочих температурах в тысячи раз превышает плотность тока в них при нормальной температуре, что определяет их использование в сильноточных электротехнических устройствах, к которым предъявляются высокие требования по надежности и взрывобезопасности.

Применение криопроводников в электрических машинах, кабелях и т.п. имеет существенное преимущество по сравнению со сверхпроводниками.

Если в сверхпроводниковых устройствах в качестве охлаждающего агента применяют жидкий гелий, работа криопроводников обеспечивается благодаря более высококипящим и дешевым хладагентам - жидкому водороду или даже жидкому азоту. Это упрощает и удешевляет производство и эксплуатацию устройства. Однако необходимо учитывать технические трудности, которые возникают при использовании жидкого водорода, образующего при определенном соотношении компонентов взрывоопасную смесь с воздухом.

В качестве криопроводников используют медь, алюминий, серебро, золото.

12Медь - один из первых металлов, которые человек начал применять для технических целей. Вместе с золотом, серебром, железом, оловом, свинцом и ртутью, медь известна людям с древнейших времен и сохраняет свое важное техническое значение до наших дней.

Медь или Сu(29)

Медь - металл розово-красного цвета, относится к группе тяжелых металлов, является отличным проводником тепла и электрического тока. Электропроводность меди в 1,7 раза выше, чем у алюминия, и в 6 раз выше, чем у железа.

Латинское название меди Cuprum произошло от названия острова Кипр, где уже в III в. до н. э. существовали медные рудники и выплавлялась медь. Около II - III в. выплавка меди производилась в широком масштабе в Египте, в Месопотамии, на Кавказе, в других странах древнего мира. Но, тем не менее, медь - далеко не самый распространенный в природе элемент: содержание меди в земной коре составляет 0,01%, а это лишь 23-е место среди всех встречающихся элементов.

Дата добавления: 2015-07-11