
|
Читайте также: |
MG = Rv2.
Откуда
G = Rv2/M = 0,2312.
Получаем очень большой (по сравнению с принятым G = 6,67·10-8) гравитационный коэффициент, равный G = 0,2312. Продублируем его получение другим способом:
G = 3 w2/ 4 pr, (6.5)
где r = 4,067·10-7, w = v/R = 6,265·10-4/
Подставляем в (6.5) и получаем:
G = 3(6,265·10-4)2 /4 p ·4,06710-7 = 0,2304.
Одинаковый результат, полученный различными способами, можно считать доказательным. Зная G, находим какова величина удельного заряда Солнца fc:
fc = vG = 0,48.
Определим величину заряда ес, которым обладает тело Солнца:
ec = fcMc = 2,756·1026.
Аналогичным образом определяем, каким зарядом обладают все планеты, и занесем эти параметры в таблицу 25.
Полученные параметры зарядов планет (табл. 25, столбец 7) по величине разбросаны в пределах почти двух порядков. (Отмечу, что никакого отдельного заряда, сосредоточенного на поверхности тел, планет, спутников и электронов не имеется. Заряд это свойство тела, его определенная физическая характеристика, связанная с пульсацией и другими свойствами, интегрированная сумма колебательных состояний всех атомов и молекул тела.). Их суммарный заряд, тот по которому в квантовой механике классифицируются атомы тел, почти на порядок меньше заряда Солнца и не очень-то понятно, как такая совокупность «зарядов» взаимодействует между собой и Солнцем ¾ по законам электродинамики или классической механики.
Таблица 25
| G' | v' | R' | f' | е' | G | f | е 1025 | ħ 1045 | ||
| Солнце | 0,2304 | 4,367·107 | 6,97·1010 | 0,48 | 2,75·1026 | - | - | - | 1,74 | |
| Меркурий | 2,18·10-9 | 2,967·105 | 2,42·108 | 4,67·10-5 | 4,54·1023 | 2,109 | 1,452 | 9,14 | 1,75 | |
| Венера | 5,15·10-8 | 7,225·105 | 6,07·108 | 2,27·10-4 | 1,39·1024 | 2,882 | 1,698 | 7,82 | 1,75 | |
| Земля | 6,65·10-8 | 7,907·105 | 6,38·108 | 2,58·10-4 | 1,54·1024 | 3,392 | 1,842 | 7,21 | 1,75 | |
| Марс | 5,24·10-10 | 3,563·105 | 3,39·108 | 7,24·10-5 | 5,95·1023 | 4,181 | 2,045 | 6,49 | 1,74 | |
| Юпитер | 7,3410-5 | 4,297·106 | 7,13·109 | 8,57·10-3 | 1,54·1025 | 7,221 | 2,687 | 4,77 | 1,75 | |
| Сатурн | 2,09·10-5 | 2,606·106 | 6,01·109 | 4,57·10-3 | 8,93·1024 | 10,46 | 3,234 | 4,10 | 1,75 | |
| Уран | 2,04·10 6 | 1,596·106 | 2,45·109 | 1,43·10-3 | 4,37·1024 | 14,88 | 3,857 | 3,45 | 1,75 | |
| Нептун | 2,88·l06 | 1,874·106 | 2,51·109 | 1,68·10-3 | 5,13·1024 | 18,55 | 4,308 | 3,08 | 1,74 | |
| Плутон | 21,25 | 4,610 | 2,87 | 1,74 |
Если провести сравнительный расчет силы взаимодействия F для любой из планет, например, Марса с Солнцем и центробежной силы от движения планеты по орбите, то полученные результаты оказываются несопоставимыми:
F=e'eс/l2 = 3,l59 1023
где ес - заряд Солнца, е' - заряд Марса, l - расстояние между их центрами, F - сила притяжения Солнцем Марса.
Найдем силу центробежного отталкивания:
F' m'v2/l = 2,1·1027 (6.6)
где т - масса планеты (таблица 21, столбец 3), v - скорость Марса на орбите.
То, что F = F' может означать, что в случае использования непосредственно массы и заряда тела планеты электромагнитное притяжение Солнца и центробежное отталкивания не имеют места, то есть Солнце не взаимодействует с планетой. Поэтому следует, как и в случае гравитационных взаимодействий, рассмотреть возможность взаимодействия заряда Солнца с динамическими массами и динамическими зарядами планет. Параметры динамической массы M, расстояния l, скорости v берем из таблицы 21 столбцы 7, 8, 9. Рассчитываем и заносим в столбцы 8, 9, 10 таблицы 25 соответственно G, f, и заряд динамического объема е каждой планеты. Постоянную Солнечной системы ħс определяем из уравнения
ħс = e2/v,
и результат записываем в столбец 11 той же таблицы.
Как и ожидалось, «заряды» динамических объемов всех планет оказались отличными от «заряда» тел самих планет, и, более того, квадрат каждого динамического «заряда», деленный на его орбитальную скорость, дает одну и ту же величину солнечной постоянной ħc = 1,746·1045, такую же, которая была получена ранее (таблица 21, столбец 10) при рассмотрении гравитационных параметров Солнечной системы.
Проведем сопоставление параметров силы взаимодействия динамических объемов планет, найденных по закону гравитационного притяжения Ньютона Fг (5.27), электромагнитных притяжений Кулона Fэ (5.26) и уравнения центробежного взаимодействия Fц (6.6) исходя из того, что ес равно по модулю е' планет, а коэффициент G = f·f':
Fг = Fэ = GMM'/l2 = е2 /l2 = 2,325·1025.
Сила, вызываемая центробежным ускорением, равна:
Fц = Mv2/l = 2,322·1025.
В данном случае результаты всех трех решений совпадают. А это означает, что собственно сами тела (планеты, спутники, электроны и т.д.) непосредственно не взаимодействуют со своими центральными телами-ядрами. Получается так, что они в значительной ме ре экранированы динамическими объемами от ядер и всякая передача энергии или силового воздействия происходит через промежуточный носитель — динамический объем, который и обусловливает количественную форму передачи соответствующего параметра. Это с одной стороны. С другой — экранирование ядра от планет-электронов превращает движение этих электронов по орбите как бы в относительное движение, при котором планеты взаимодействуют только с вещественным пространством независимо от своих ядер и потому энергия их движения соответствует в первую очередь количественным величинам свойств окружающего пространства. Планета электрон оказывается как бы «погруженной» в некую движущуюся с той же скоростью вещественную «глобулу», и гравитационные и электрические воздействие на ее параметры передаются только через эту «глобулу». (Именно это совместное движение Земли и эфира ее глобулы фиксируется в опыте Майкельсона-Морли и в других экспериментах. [ 152 ]) И можно сделать следующие предварительные выводы:
• электрические и гравитационные параметры небесных тел отображают различную форму одних и тех же взаимодействий;
• планета-электрон в своем движении по орбите и вращении «увлекает» вещественный эфир в объеме равном тому объему, который остается «неподвижным» в пространстве от Солнца до ее орбиты;
• собственные параметры тел планет (G', v', R', f', e') на орбитах различаются в пределах порядка, тогда как динамические параметры (G, f, e) монотонно возрастают или уменьшаются на одинаковом расстоянии от центрального тела строго на один и тот же КФР, отграничивая и затушевывая тем самым количественную величину их индивидуальных свойств. Отсюда следует, что модули всех свойств тел не могут быть тождественны друг другу;
• собственные масса и заряд тел, находящихся внутри динамических объемов (глобул), практически ничем не проявляют себя на их границах, кроме скорости движения глобул. И потому глобулы тел электронов, дви жущиеся в пространстве с одинаковой скоростью, имеют равные по модулю параметры и фиксируются приборами как абсолютно тождественные частицы. Именно эти обстоятельства и обусловили постулирование всем элементарным частицам отсутствующего в природе свойства тождественности;
• суммарный «заряд» всех планет Солнечной системы значительно меньше заряда самого Солнца и следовательно, либо в ней имеются другие заряды компенсирующие недостаток, либо количество зарядов не имеет существенного значения для системы;
• в отличие от гравитационных масс тел-планет, которые на два порядка превышают массы глобул (таблица 21, столбцы 5 и 7, что свидетельствует об отсутствии непосредственного влияния масс на притяжение тел), электрический заряд динамических объемов-глобул, похоже, во всех случаях оказывается по количественной величине больше зарядов тел своих планет;
• принадлежность системам планет некоторой системы зарядов обусловливает возможность иного подхода к рассмотрению механизма гравитационного и электромагнитного взаимодействий.
Теперь, имея модель атома с планетами-электронами и зная в соответствии с квантовой механикой, что электроны вращаясь по орбитам вокруг ядра-Солнца, не излучают энергии (т.е. вращаются с « нарушением» законов электродинамики), рассмотрим, принимая систему из двух тел планета-Солнце за диполь, как скоро планета, например Земля, упадет на Солнце, если исходить из уравнения (5.4):
t = rо (ао/rо) 3 / 4 со, (5.4)
здесь хо = 6,378·108 см - радиус планеты, ао = 1,496·1013 см - радиус орбиты, со = 4,58·108 см/с - скорость электромагнитных волн у поверхности планеты.
Подставляем параметры в (5.4) и получаем t:
t = 6,378·108(1,496·1013/6,378·108)3/(4·4,58·108) =
= 4,493·1012 с. или 142,4 тыс. лет.
Итак, время существования планеты Земля от зарождения и до падения на поверхность Солнца составляет «по законам электродинамики» всего 142,4 тыс. лет, что явно противоречит геологическим данным и свидетельствует об ошибочности уравнения (5.4), а следовательно, и о некорректности предположения о нарушении электронами, законов электродинамики и нестабильности электронных орбит в атоме, послуживших первым шагом для формулирования квантовых постулатов.
6.4. Элементы самодвижения
космических тел
Если рассматривать движение тел в плотном вещественном пространстве, то сразу же возникает вопрос о том, как твердое тело движется в веществе без заметного изменения скорости своего движения. Иначе говоря: Почему вещество пространства не тормозит его движения? Ответа на этот вопрос еще не найдено. Более того, поскольку космическое пространство, по современным представлениям, является пустым объемом, заполненным флуктуациями электромагнитных полей, то и сопротивления движению тел в нем ничто не оказывает, а следовательно, и вопроса не возникает и искать нечего. Но эта наивная точка зрения постепенно утрачивается и до конца не исчезла именно потому, что неизвестен механизм, обеспечивающий движение вещества в веществе без сопротивления данному движению.
Признание самопульсации тел и наличия вокруг них эфирных глобул позволяет выдвинуть гипотезу механизма взаимодействия планет, и в принципе подойти к решению этой задачи на примере движения планет вокруг Солнца. Механизм этот далее будет качественно изложен. Сейчас же еще раз отмечу, что существование вокруг Солнца и планет эфирных глобул, имеющих (если рассматривать с позиций классической механики) для каждой пары планета-Солнце одинаковую массу и объем, но разную величину массы собственного тела, выглядит для физиков весьма необычно. Еще необычнее то, что эти небесные тела имеют разную величину заряда и, в полном соответствии с электродинамикой, разные знаки.
Существование глобул, движущихся вместе с планетой вокруг Солнца и имеющих гигантские по сравнению с планетами объемы, но намного меньшие количественные величины масс и других параметров, чем тела самих планет, обусловливает необходимость рассмотрения элементов, движения планет и механики ее взаимодействия с другими телами иначе, чем это трактуется современной механикой. Возникает целый ряд вопросов, связанных с таким движением. Например: тело планеты движется по орбите вместе с глобулой и находится внутри ее. Следовательно, относительно вещественного пространства глобулы оно неподвижна, а перемещение динамического объема глобулы «определяется» взаимодействием «границ» ее плотности с плотностью окружающего пространства. А где эта граница? Если исходить из инварианта (6.1) распределения пространственной плотности эфира, то граница глобулы между Солнцем и Землей определяется сравнительно легко. Она, похоже, находится на половине расстояния между ними 1/2 = 7,48·1012 см там, где плотности эфира от Солнца и Земли оказываются одинаковыми.
Однако в сторону, противоположную от Солнца» так же как и по траектории орбиты Земли со стороны, противоположной ее движению, эта граница как бы расплывается. В направлении же движения Земли граница глобулы должна быть четко выраженной. Это происходит потому, что движущийся с глобулой эфир «сминает» вдоль орбиты «неподвижный» эфир солнечной глобулы.; В результате «смятия» на орбите впереди планеты возникает эфирная ударная волна, резко отграничивающая движущуюся глобулу от «неподвижного» эфира. Фактор образования ударной эфирной волны впереди движущегося тела, видимо, выполняет главную роль в обеспечении его движения. Прежде чем рассматривать этот фактор, отметим еще раз, что движение есть следствие направленной пульсации тела. Или иначе — процесс движения есть следствие волнового взаимодействия тела с пространством и в направлении движения, и в противопо-ложном направлении.
Волновое взаимодействие, в свою очередь, предполагает, что во всех направлениях и в первую очередь в направлении движения тела волна от него движется быстрее, чем само тело: И быстрее намного. Вот этот-то фактор движения волны в эфире на сегодня и не фиксируется ни эмпирически, ни теоретически. Посмотрим, существует ли возможность определения скорости эфирной волны, например, от Земли в направлении ее движения по орбите.
Ранее было предположено, что граница глобулы находится от планеты на расстоянии, равном расстоянию от центра Земли до центра Солнца. Учитывая, что глобула движется как единое тело с плотностью, уменьшающейся к границам, а скорость ее движения такая же, как и у Земли, то и скорость движения эфирных волн от поверхности к границам должна уменьшаться пропорционально плотности. То есть скорость движения волн определякется плотностью вещественного пространства, сквозь которое проходит волна. Это предположение подтверждается инвариантом зависимости скорости волны v от плотности r. Инвариант имеет следующий вид:
r/v - const. (6.7)
Покажу, что, не используя инварианта зависимости скорости от расстояния (2.29), можно по (6.7) определить скорость движения волны от центрального тела в любой области пространства, если в ней известна плотность r. Зная скорость вращения гравиполя Солнца vc = 4,37·1О7 см/с и плотность у поверхности Солнца rс = 4,067·10-7 г/см3, а также плотность в районе либрационной точки r = 2,793·10-15 г/см3, можно определить орбитальную скорость Земли. Подставляя в (6.7) числовое значение r и v, определяем const:
r / v7 = 4,067·10-7/(4,367·107)7 = 1,343·10-60. (6.8)
Подставляем в (6.8) величину r и определяем орбитальную скорость v1 глобулы Земли;
v1 = 7Ö (rс /1,343·1060) = 2,979·106 см/с.
Результат в точности соответствует скорости движения Земли по орбите. Это соответствие можно считать доказательством зависимости скорости движения гравитационных волн от плотности того пространства, по которому они проходят. Исходя из этого определим, используя инвариант (6.8), с какой скоростью v2 они начинают двигаться от Земли, зная, что плотность эфира у Земли r2 = 5,52 г/см3:
v2 = 7Ö(r2 /1,343·10-60) = 4,562·108 см/c.
Линейная скорость гравипульсации Земли оказывается на порядок больше линейной скорости гравиполя Солнца. Это кажется неправдоподобным, но именно в этом случае волна, двигаясь от Земли в глобуле, будет иметь скорость около 30 км/с на ее границе в либрационной точке. Чтобы убедиться в правильности полученного результата, найдем скорость v2 другим способом по инварианту (2.29) lv2 = const':
lv2 = l,496·1013(2,989·106)2 = l,336·1026. (6.9)
Подставляем в инвариант (6.9) величину радиуса Земли:
v2 = v (1,336·1026/6,378·106 = 4,58·108 см/с.
Получаем ту же скорость 4,58·108 см/с. Эта скорость по порядку величины сопоставима со скоростью электронов на внешних орбитах атомов (таблица 11). Учитывая эти пропорции, можно предположить, что движение Земли на орбите обусловливает именно объемное интегрированное воздействие самопульсации ее молекул (атомов?), распространяющееся от поверхности во все стороны с начальной скоростью 4,562·108 см/с. Определим по инварианту (6.7) или (2.29), какую линейную скорость гравиполя v2 имеют у своей поверхности остальные планеты, и занесем эти параметры в таблицу 26 столбец 3. Отметим, что линейная скорость вращения гравитационного поля всех планет в пределах порядка одинакова и близка к тем скоростям, которые приборно регистрируются у электронов (отмечу, что мне еще не встречались в литературе случаи наблюдения у электронов скоростей меньше 107 см/сек; если они не регистрируются, то это может означать наличие природного ограничения на скорости, связанные со структурой атомов). Она в среднем на порядок превышает скорость вращения гравиполя у поверхности Солнца.
Таблица 26
| v2 см/с | vгр см/с | v2/vrp | rj /lop | Рт | ||
| Солнце | 4,367·107 | 4,18·1044 | ||||
| Меркурий | 7,400·108 | 2,967·105 | 4,188·10-5 | 4,06·1040 | ||
| Венера | 4,676·108 | 7,225·105 | 644,4 | 5,610·10-5 | 1,97·1041 | |
| Земля | 4,562·108 | 7.910·105 | 4,263·10-5 | 2,24·1041 | ||
| Марс | 6,252·108 | 3,563·105 | 1754,5 | 1,489·10-5 | 6,30·1040 | |
| Юпитер | 1,364·108 | 4,297·106 | 31,7 | 9,161·l0-5 | 7,47·1042 | |
| Сатурн | 1,486·108 | 2,606·106 | 57,02 | 4,212·10-5 | 3,99 ·1042 | |
| Уран | 2,327·108 | 1,596·106 | 145,8 | 8,539·10-6 | 1,42·1042 | |
| Нептун | 2,299·108 | 1,874·106 | 122,6 | 5,581·10-6 | 3,55·1042 | |
| Плутон- | 6,440·108 |
Из столбца 3 табл. 26 следует вывод о том, что линейная скорость вращения гравиполей тел, находящихся на орбитах вокруг Солнца, должна примерно на порядок превышать скорость вращения его гравиполя. И возникает вопрос: А сохраняется ли эта пропорция для спутников планет, особенно у тех из них, у которых размеры спутников имеют «солидный» разброс по величине радиуса. Рассчитаем скорости гравиполей v2 у поверхностей спутников Юпитера и занесем их в табл. 27.
|
Таблица 27
| v2 | rсп/lор | ||
| Юпитер | 1,364·108 | ||
| Амальтея | 4,073·109 | 4,420·10-4 | |
| Ио | 8,746·108 | 4,121·10-3 | |
| Европа | 9,253·108 | 2,310·10-3 | |
| Ганнимед | 7,286·108 | 2,336·10-3 | |
| Каллисто | 7,515·108 | 1,248·10-3 | |
| Атлас | 4,703·109 | 5,263·10-6 | |
| Прометей | 1,487·1010 | 5,124·10-6 | |
| Геракл | 8,139·109 | 1,709·10-6 | |
| Гефес | 1,553·1010 | 2,657·10-7 | |
| Дедал | 1,330·1010 | 3,355·10-7 | |
| Прозерпина | 1,553·1010 | 2,300·10-7 | |
| Цербер | 1,377·1010 | 2,953·10-7 |
Получается так, что линейная скорость вращения гравиполей малых спутников Юпитера приближается к скорости света, к скорости, которую электроны в естественных условиях достигают только внутри атомов и молекул либо в искусственных условиях в синхрофазотроне и, следовательно, надо ожидать, что и плотность пространства в камере синхрофазотрона соответствует плотности у поверхности этих «камешков»-спутников.
Отмечу, что интересная «случайность» (?) наблюдается в отношении приповерхностной скорости вращения гравиполя Земли v'1 = 7,91·105 см/с к аналогичной электромагнитной скорости ее же v2 = 4,562·108 см/с. Если вторую разделить на первую, то получим:
v2/v1' = 4,562·108/7,91·105 = 576.
Безразмерное число 576 можно записать в виде; 576 = 4pa/3, где a ≈ a' = 137,5 > 137,04 всего на 0,3%. Если учесть, что a - постоянная тонкой структуры в квантовой механике и вспомнить, что 4 pa - нижняя граница трехмерности, то это достаточно странное и вызывающее много вопросов совпадение. Но вернемся к Земле.
Попробуем промоделировать качественно, как «разбегаются» волны в пространстве от пульсирующей Земли. Отметим, что длина волны, амплитуда и частота, но не фаза, от Солнца и от Земли, полученные по инварианту (2.29) длины волн l, будут иметь в либрационной точке одинаковую величину. По этому же инварианту длина волны и амплитуда от Солнца и Земли на середине расстояния между ними тоже оказываются одинаковой величины. И чтобы Солнце и Земля не притягивали и не отталкивали друг друга, достаточно, чтобы их амплитуды совпадали по величине и фазе, но имели разный знак, т.е. силы F1 = F1' обусловленные волнами, взаимно погашались (рис. 71). Это обстоятельство и обеспечивает Земле устойчивое положение на орбите.
Рис. 71.
Волна, вызываемая самопульсацией Земли, объемна. Ее часть, идущая в сторону от Солнца (в направлении F3), будет давать Земле дополнительный импульс, «прижимая» ее к Солнцу. Такой же импульс она получает и от волн, движущихся по направлению ее движения по орбите и против этого направления. То есть с двух сторон по орбите возникают одинаковые взаимопогашающие силы F2 = F4, и, следовательно, Земля тоже должна оставаться на месте.
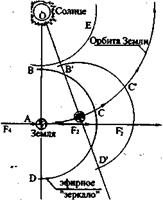
Это в случае ее неподвижности относительно Солнца. В случае ее движения энергия волн самопульсации по направлению движения больше, чем поперек его. Но и в этом случае сила F1, образуемая по направлению движения, равна силе F4 , направленной в противоположную сторону. А потому кажется, даже без учета сопротивления эфира, что планета не может двигаться за счет отталкивания от пространства. И все же она движется. Более того, образует в направлении движения впереди «себя», как уже упоминалось, бегущую ударную сферическую волну, «сминающую» и уплотняющую эфирное пространство перед движущимся телом (Образуя своего рода сферическую стенку плотности). Похоже, что это «смятое» вещественное пространство и становится основным элементом, обеспечивающим движение небесного тела в пространстве. Плотность «ударной» волны оказывается такой величины, что становится непреодолимой для набегающей на нее от тела (Земли, в частности) электромагнитной волны самопульсации. Более того, набежавшая волна этой сферической стенкой полностью отражается и с «фокусировкой» «возвращается» в сторону Земли. Отраженная волна с двойной силой воздействует на сферическое «зеркало», уплотняя «тело» последней и обеспечивая ее дальнейшее, как бы независимое от планеты, движение (рис. 72).
|
В свою очередь отраженная космическим «зеркалом» электромаг-нитная волна возвращается к телу (к поверхности Земли), имея те же параметры,что и движущаяся ей на
встречу волна самопульсации. В результате на всем пространстве от «зеркала» до Земли образуются стоячие волны, обусловливающие притяжение Земли к «зеркалу» и «зер- кала» к Земле. Сила F2 оказывается скомпенсированной этим притяжением
Дата добавления: 2015-07-11; просмотров: 53 | Нарушение авторских прав