Положение равновесия.

Лекция 13. Механические колебания.

Современная теория колебаний – это очень большой раздел теоретической механики. В ней исследуются различные виды колебаний: свободные, вынужденные, параметрические, автоколебания.

Различаются колебания линейные и нелинейные – в зависимости от типа дифференциальных уравнений этих колебаний.

Изучим простейшие колебания - свободные (без сопротивления и с сопротивлением).

Положение равновесия.

Из опыта известно, что колебания всегда возникают вблизи положения равновесия. Вопрос о поиске положения равновесия для механических систем с голономными, стационарными, идеальными и удерживающими связями решается на основе принципа Лагранжа.

Для механической системы с обобщенными координатами 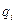в положении равновесия все обобщенные силы равны нулю: 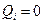. Будем рассматривать прежде всего системы, в которых действуют только потенциальные и диссипативные силы. Диссипативные силы как силы, пропорциональные скоростям точек, не влияют на положение равновесия. Таким образом, положение равновесия определяется только потенциальными силами, т.е. на основании принципа Лагранжа-Дирихле для механических консервативных систем: . Эти уравнения можно рассматривать как систему 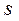уравнений с 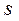неизвестными 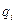. Решения этой системы и определяют положение равновесия.

ПРИМЕР Обращенный маятник.

Строгое определение понятия устойчивости дано А.М.Ляпуновым. Достаточные условия устойчивости для консервативных механических систем дает теорема Лагранжа-Дирихле, которая может быть получена как следствие из общей теоремы Ляпунова об устойчивости.

Теорема: Если в положении равновесия консервативной механической системы потенциальная энергия имеет минимум, то это положение устойчиво. Таким образом, для того чтобы установить факт устойчивости данного положения равновесия системы, достаточно убедиться в том, что в этом положении энергия имеет минимум. Для системы с одной степенью свободы это делается элементарно.

Если первая, не травная нулю производная имеет четный порядок, то по ее знаку можно определить, минимум или максимум имеет функция: производная положительная - минимум, отрицательная – максимум. Если же первая не равная нулю производная имеет нечетный порядок, то функция в этой точке не имеет ни минимума, ни максимума. Таким образом, если вторая производная от потенциальной энергии 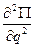оказывается в положении равновесия положительной, то такое положение устойчиво.

ПРИМЕР. Обращенный маятник.

Переходом к малым колебаниям называется приближенный метод описания явления колебаний, связанный с линеаризацией системы уравнений.

Дата добавления: 2015-07-11