Найдем фазовой портрет гармонического осциллятора с вязким трением.

В гармоническом осцилляторе с вязким трением к восстанавливающей силе добавляется сила сопротивления, пропорциональной первой степени скорости и направленная в сторону, противоположную скорости. Дифференциальное уравнение движения системы

, где , - коэффициент пропорциональности силы сопротивления.

Обозначив как и ранее, 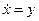перепишем уравнение в виде системы двух уравнений , 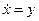. Исключив время, находим 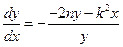. Отсюда следует, что особой точкой является начало координат – положение равновесия. Чтобы отделить переменные, произведем замену . Тогда уравнение примет вид .

Интеграл этого уравнения зависит от вида корней квадратного полинома в знаменателе правой части. Поэтому рассмотрим два случая: - случай малого сопротивления и - случай большого сопротивления, к которому примыкает и граничный случай .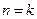

Случай малого сопротивления: Интегральные кривые – скручивающиеся спирали, навивающиеся на начало координат. Особая точка в этом случае называется устойчивым фокусом. Изображающая точка приближается к началу координат асимтотически. (Рисунок)

Случай большого сопротивления: В этом случае каждая интегральная кривая включает три фазовые траектории: ветвь, ведущую в начало координат справа, ветвь, ведущую в начало координат слева и особую точку. В данном случае по всем фазовым траекториям изображающая точка движется в начало координат, к особой точке – устойчивому узлу. (Рисунок)

Вынужденные колебания.

Рассмотрим колебания в системе, на которую действует некоторое переменное внешнее поле; такие колебания называются вынужденными. Поскольку колебания предполагаются малыми, то тем самым подразумевается, что внешнее поле достаточно слабое, в противном случае оно могло бы вызвать слишком большое смещение.

Обозначим обобщенную вынуждающую силу . Тогда уравнение Лагранжа второго рода будет . Полагая отклонение системы от положения устойчивого равновесия малыми, можно представить кинетическую и потенциальную энергию в виде

, , где и - инерционный и квазиупругий коэффициенты. Вводя значения для кинетической и потенциальной энергии в уравнение Лагранжа, получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами , или , где введено обозначение .

Рассмотрим случай, когда вынуждающая сила является периодической функцией времени с частотой 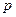: 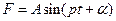. Дифференциальное уравнение колебаний материальной точки в этом случае имеет вид , где .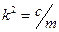

Как известно, общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами получается в виде двух выражений: 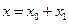, где - общее решение однородного уравнения, а - частный интеграл неоднородного уравнения.

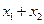Закон движения материальной точки в случае дается выражением , где

(общее решение однородного уравнения), (частное решение неоднородного уравнения).

При начальных условиях 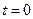, , 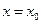постоянные интегрирования: 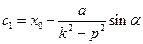и .

Окончательно уравнение движения имеет вид

- + .

Последний член в правой части определяет вынужденные колебания, первые два слагаемых определяют свободные колебания, которые совершались бы при отсутствии возмущающей силы, а слагаемое - колебания, имеющие частоты свободных и вызванных возмущающей силой. Амплитуда колебаний .

В случае резонанса, т.е. при , частное решение имеет вид 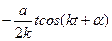, При резонансе амплитуда вынужденных колебаний возрастает прямо пропорционально времени . Общее уравнение движения при имеет вид

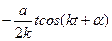- . Член определяет колебания, вызванные возмущающей силой, имеющие круговую частоту свободных колебаний.

Вынужденные колебания при наличии сопротивления .

Свободные колебания системы с двумя степенями свободы. Рассмотрим малые колебания механической системы с двумя степенями свободы, подчиненной голономным идеальным и стационарным связям. Обозначим обобщенные координаты через 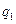и . Кинетическая энергия будет однородной квадратичной формой обобщенных скоростей 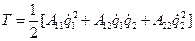. В этой формуле коэффициенты являются функцией обобщенных координат. Положение равновесия примем за начало координат. Следовательно, в положении равновесия все обобщенные координаты равны нулю. Раскладываем каждый коэффициент в ряд Маклорена по степеням обобщенных координат, ограничиваемся в разложении первым слагаемым, так как обобщенные координаты и скорости считаются малыми величинами, и обозначая для краткости постоянные коэффициенты 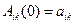, находим окончательное выражение для кинетической энергии

.

Потенциальная энергия системы, совершающей малые колебания около положения устойчивого равновесия, будет однородной квадратичной формой обобщенных координат:

, где для краткости .

Внося полученные значения кинетической и потенциальной энергий в уравнения Лагранжа, находим дифференциальные уравнения движения системы:

Частное решение ищем в виде , .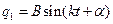

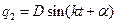Подставляя эти выражения в дифференциальные уравнения и приравнивая к нулю коэффициенты при , после ряда преобразований приходим к биквадратному уравнению для частот. Величины 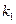и являются собственными частотами, меньшая из них 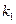обычно называется основной частотой. Каждой из частот соответствует свое решение исходной системы уравнений. Эти решения называются главными колебаниями.

, , , .

Таким образом, свободные колебания системы с двумя степенями свободы представляет собой наложение двух колебаний с двумя разными частотами. Эти часты не зависит от начальных условий и определяются только характеристиками самой системы.

------------------------------------------------------------------------------

Дата добавления: 2015-07-11